计及风电功率预测误差与需求响应的电力系统滚动调度

2018-12-20史光耀邱晓燕赵劲帅马菁曼

现代电力 2018年6期

史光耀，邱晓燕，赵劲帅，马菁曼

(四川大学电气信息学院，四川成都 610065)

0 引言

随着生态环境污染的加剧以及化石能源的日益枯竭，清洁能源在电力系统中的地位愈发重要，风能作为重要的清洁能源，其应用近年来在国内得到快速发展[1]。但风电的不确定性会导致系统运行成本上升，弃风率增加等问题。传统的解决办法一般是通过火电机组预留备用容量来应对，然而如何合理设置备用容量存在争论，备用容量过大则大幅增加了系统运行成本，备用容量过小则会引起弃风或对系统可靠性带来影响[2]。

诸多学者针对考虑风电不确定性的电力系统调度运行问题展开研究。文献[3]针对考虑风电不确定性并网带来的问题，根据机会约束规划理论建立经济调度模型，算例结果表明置信水平影响运行成本。文献[4]建立了考虑风电不确定性的电力系统多目标调度模型，通过合理安排火电机组启停计划提高运行效率，实现了系统运行的经济性与可靠性。文献[5]考虑风电的不确定性会造成系统的备用容量增加，通过建立滚动调度模型，大幅减少了系统预留备用，提高了系统的经济性。

上述研究试图从各个方面解决该问题，有些学者从风电功率预测误差的时间尺度特性着手，将风电功率的预测时刻与被预测时刻之间的时间差定义为预测超前时间，根据文献[6]可知风电功率的预测误差随着预测超前时间的减小而减小，因此可以通过制定滚动调度策略，以减少风电不确定性带来的影响。随着智能电网的深入建设与电力市场的放开，需求侧资源开始参与到电力系统的调度运行中，需求响应(Demand response，DR)是需求侧资源参与电力系统调度运行的具体表现方式。文献[7]为解决风电出力不确定性问题，建立需求响应参与下的风电消纳鲁棒随机优化模型。文献[8]建立两阶段随机规划风电消纳机组组合模型，可以在一定程度上解决风电出力不确定性的影响。需求响应在解决风电出力不确定性问题中得到了一些应用，考虑到需求响应具有时间尺度特性，因此可以按照其不同的时间尺度特性参与系统的调度运行。

本文在文献[5]提出的滚动调度模型基础上，提出一种计及风电功率预测误差和需求响应时间尺度特性的滚动调度策略，在日前调度阶段引入基于日前小时电价(Day-ahead hourly varying price，DAP)的价格型需求响应，通过场景分析法处理风电功率的不确定性，在运行成本中考虑火电机组运行的环境成本，以日前调度计划阶段确定的火电机组运行状态为基础，在日内滚动调度计划中将风电功率的更新为短期预测数据。最后通过算例对所提调度策略的有效性进行验证，结果表明该策略使负荷曲线得到改善，同时促进了风电消纳并提高了系统运行的经济性。

1 多时间尺度需求响应模型

DR按照实施方式的不同可以分为价格型需求响应(Price-based DR，PDR)和激励型需求响应(Incentive-based DR，IDR)[8]。不同类型的负荷参与DR的方式与能力不同，有些类型的负荷能够快速响应调度中心发出的调度信号以及电价的变化，有些负荷则需要提前被告知调度计划或者电价，给予其准备时间，提前制定用电计划才能做出响应。可以得出DR具有多时间尺度的特性，按照实施方式不同可以分为如下两个模型。

1.1 PDR多时间尺度模型

PDR按照电价的制定方式不同具有不同的时间尺度，制定方式包括分时电价(Time-of-use，TOU)、尖峰电价(Critical-peak-pricing，CPP)、实时电价(Real-time-pricing，RTP)，其中采用RTP方式，具有响应速度快，响应方式灵活的特点，但该方式较为理想化，实施难度高且响应的不确定性大[9]。采用TOU和CPP方式具有实施简单，响应效果明显等特点，但是对于负荷的调整缺乏灵活性。为了兼顾上述两者的优点，本文采用其他学者所提出的日前小时电价制定方式[10]，将一日内的电价分为24个时段，根据次日风电预测功率及负荷预测值制定各时段电价，用户作出响应提前确定用电计划，可知该方式下的DR的时间尺度为1d。在实施DAP的前提下，基于统计学原理对用户参与PDR行为进行建模，根据历史负荷数据与电价的关系，拟合后得到用户参与PDR后的负荷值与售电电价的关系如下式：

(1)

式中：PD,t表示t时段的原始负荷值；α表示参与PDR的负荷占总负荷的比例；rt表示实施PDR后t时段的电价；rs表示实施PDR前的原始电价；PD,act,t表示实施PDR后t时段的负荷值。

从电力公司的角度，用户参与PDR的调度成本CPDR为

(2)

式中：T表示一个调度周期的调度时段数。

1.2 IDR多时间尺度模型

本文中能够参与IDR 的负荷根据需要提前被告知调度计划的时间不同可以分为两类[5]：

① 1类IDR：需提前1d告知用户；

② 2类IDR：需提前2h告知用户。

可知两类IDR的时间尺度分别为1d和2h，用户参与IDR的调度成本分为容量成本与电量成本两部分，电量成本根据IDR用户阶梯报价曲线求解，如图1所示，据此可知IDR的调度成本CIDR,j为

(3)

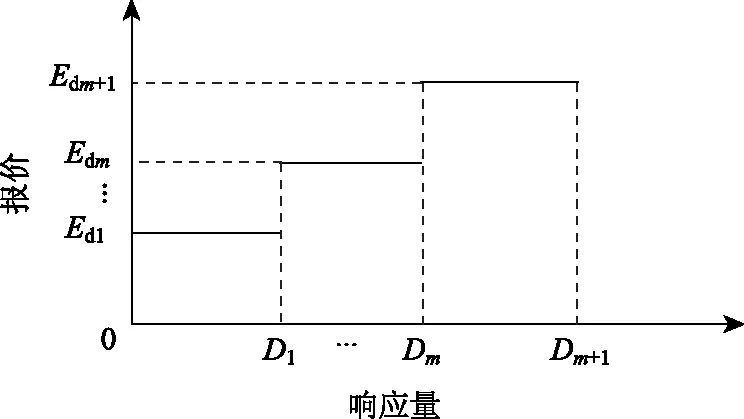
图1 IDR用户报价曲线Fig.1 IDR user’s quote curve

2 风电功率不确定性模型

研究表明实际风电功率可以表示为风电预测功率与误差之和[11]，假设t时段的风电功率为随机变量PWT,t：

PWT,t=PWT,t,f+ΔPWT,t

(4)

本文采用基于场景分析的随机规划法[8,12]，解决考虑风电不确定性的调度问题，通过生成多个风电场景，使得决策量在多个场景均能满足要求，选择使所有场景期望成本之和最小的调度策略作为最优解。根据PWT,t的分布模型，运用蒙特卡洛随机抽样技术随机生成多个风电输出功率场景，运用同步回代消除法[13]对场景进行削减至Ns个场景，则最终求得的最优解Ffinal表示为

(5)

式中：Pr(s)表示第s个场景发生的概率；Fs表示第s个场景下的最优解。

3 计及需求响应时间尺度特性的滚动调度模型

本文提出一种日前-日内的滚动调度策略，在日前调度计划的基础上，增加日内滚动修正计划，同时考虑需求响应的多时间尺度特性，实现了多时间尺度下火电机组与需求侧资源的最优经济配置。图2展示了滚动调度策略的实施流程。

图2 滚动调度计划实施流程Fig.2 Process of rolling scheduling plan

日前调度计划每1d进行一次，在该阶段根据负荷以及日前风电的预测数据，不考虑风电功率的不确定性，以系统的运行成本最低为目标，在该阶段需要确定的调度量为：火电机组的出力；PDR的调用量；1类IDR的调用量。

日内滚动调度计划每2h执行一次，日前阶段确定的传统机组、PDR、1类IDR调度量作为已知量参与到该阶段计划，将风电功率更新为预测超前时间为2h的短期预测数据，同时考虑其不确定性，以系统运行成本最低为目标，确定2类IDR的调度计划，至此整个滚动调度计划的实施流程结束。

3.1 日前调度模型

3.1.1 目标函数

日前调度计划模型中考虑火电机组的环境成本，同时加入弃风惩罚项，目标函数为

minF1=CG+CG,EC+CPDR+

(6)

式中：CG表示火电机组发电成本，参照文献[11]采用二次函数表示；CG,EC表示火电机组发电的环境成本；PWT,loss,t表示t时段的弃风量；λWT,loss表示弃风惩罚系数。

火电机组发电的环境成本计算公式如下[14]：

(7)

式中：Ve,k表示第k类污染物的污染成本；n表示排放的污染物种类；Qk表示每单位发电量第k类污染物的排放量；WG,t表示t时段火电机组发电量之和；Vk表示第k类污染物的超标排放惩罚额度。

3.1.2 约束条件

① 系统有功功率平衡约束：

PG,t+PWT,t,f-PWT,loss,t=PD,act,t+

(8)

式中：PG,t表示t时段火电机组出力之和。

② 火电机组出力约束：

火电机组的主要约束有出力上下限约束、爬坡约束以及旋转备用约束，详细可见文献[11]。

③PDR约束：

最大、最小电价约束：

rmin≤rt≤rmax

(9)

负荷的调整速率约束：

(10)

式中：rup和rdown分别表示表示一个调度时段间隔Δt内的负荷增加和减少的最大速率。

一个调度周期内用户负荷总量平衡约束：

(11)

④IDR约束：

(12)

(13)

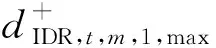
3.2 日内滚动调度模型

3.2.1 目标函数

滚动调度是一个多时间尺度优化问题，其调度目标仍为系统运行成本最低，在日前调度阶段所确定的已知量基础上，求得使所有场景期望成本之和最小的调度策略，该阶段的目标函数为

(14)

(15)

3.2.2 约束条件

① 系统有功功率平衡约束：

PG,t+PWT,t,f-PWT,loss,t,s=PD,act,t+

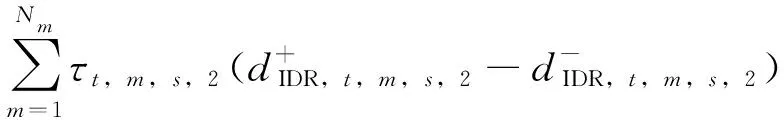
(16)

② IDR约束：

(17)

(18)

4 算例分析

4.1 算例参数

本文算例采用IEEE30节点6机系统，包含1个风电场。负荷预测数据、风电功率预测数据、火电机组的相关运行参数等数据参考文献[15]，负荷与风电功率预测曲线如图3所示，采用蒙特卡洛方法随机生成1 000个风电场景，经过削减后的风电场景数s取10个，弃风惩罚系数[8]λWT,loss取500元/MWh。参与PDR的用户占比α取值10%，rs取0.6元/kWh，rmin取0.3元/kWh，rmax取0.9元/kWh。1类IDR与2类IDR每时段增减电量的上限分别为±20MW和±10MW，IDR负荷聚合商的报价曲线参数见表1。根据风电日前以及短期预测精度[16]，取日前和短期误差δWT,t分别为0.2PWT,t,f和0.05PWT,t,f，随机生成一组误差，图4给出了不同预测超前时间下风电功率的预测误差的对比。算例采用在Matlab软件中调用Cplex软件进行求解。

表1 IDR聚合商报价参数Tab.1 Parameters of IDR aggregator quotation

图3 负荷预测与风电功率预测图Fig.3 Load prediction and wind power prediction curve

图4 不同预测超前时间风电功率预测误差对比Fig.4 Comparison of different prediction of advance time wind power prediction error

4.2 仿真结果分析

根据给定算例参数，按照所制定的滚动调度流程，进行日前调度计划，在此阶段确定的DAP优化电价曲线如图5所示，用户响应PDR后的负荷曲线如图6所示。由图5和图6可以看出，实施DAP后会改变用户的负荷曲线，负荷的峰谷差值下降26.7%，负荷的均方差值下降57.4%，可见实施DAP可以明显地减小负荷的峰谷差，改善负荷的波动性。

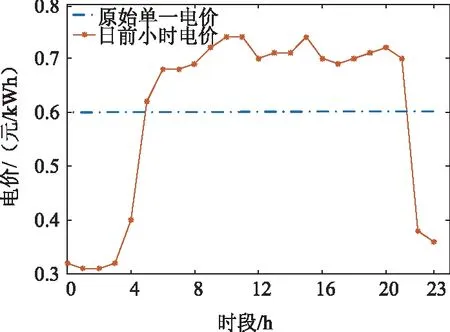
图5 DAP优化电价曲线Fig.5 Optimization price of DAP

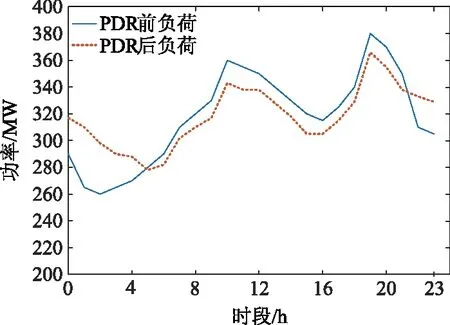
图6 PDR前后负荷曲线Fig.6 Load curve of before and after PDR

进行滚动调度计划，最终得到各类型DR的调用情况如图7所示。由图中可以看出PDR与1类IDR主要起削峰填谷的作用，在用户用电的高峰期(5:00～21：00)减少用电量，在用电的低谷期(22:00～4：00)增加用电量，使负荷从高峰期转移到低谷期，可以用来改善长时间尺度下的风电反调峰特性。2类IDR在整个调度周期内波动较为剧烈，主要用来减轻风电不确定性带来的影响，平抑风电的波动性。3类DR资源的调用总量顺序为：PDR>IDR1>IDR2，这是由于PDR调用成本较低，1类IDR次之，2类IDR的调用成本最高，这样的调用策略下系统运行的经济性最佳。

图7 各类DR调用情况Fig.7 Dispatch result of DR

为了更加直观展现风电的不确定性对系统运行带来的影响及本文所提出策略的有效性，本文对比了3种调度运行模式：模式1采取不考虑风电的不确定性的传统日前调度运行方式，模式2采取考虑风电不确定性的传统日前调度运行方式，模式3采取本文所提的时间尺度特性的滚动调度运行方式。表2给出了3种模式下的调度结果对比。

表2 3种模式下调度结果对比Tab.2 Comparison of scheduling results under three modes

由表2中模式1与模式2调度结果的对比可以看出，考虑风电不确定性后，系统的各项成本均有所增加，弃风率提高，风电的不确定性对系统的调度运行带来严重的影响。模式2与模式3的结果显示采用本文所提出的滚动调度策略可以显著减少弃风电量，增加风电消纳率。系统清洁能源的渗透率增加，火电机组的运行成本以及系统的环境成本有所降低，体现了风电作为清洁能源在环保方面的优势。虽然调用DR资源增加了部分调度成本，但是系统的最终总运行成本有较为明显的降低，证明了本文所提调度策略的有效性。