基于参数化方法的水下拖缆微元阻力分析

2018-12-20孙现有刘显龙

数字海洋与水下攻防 2018年3期

孙现有，刘显龙

(1.海军驻昆明七五〇试验场军事代表室；2.中国船舶重工集团公司七五〇试验场，云南昆明 650051)

0 引言

拖缆作为水面及水下武器的承载设备发挥着巨大的作用。常见的拖缆拖曳形式有水面舰拖曳航行体，水下航行体拖曳声学线列阵等。为了计算整个拖缆的阻力性能，需要将其参数化，计算各个的阻力性能，并将其整体矢量求和。

以往常采用经验公式法来计算拖缆微元的阻力性能[1]。经验公式是将来流速度按拖缆的切向、法向2个方向进行分解，再由公式计算切向力和法向力[2]。采用这种方法由于未考虑切向与法向速度相互干扰因素，结果不够准确，连琏等人[3]通过试验的方法严格说明了此种方法带来的误差，本文不再赘述。随着计算流体力学(CFD)技术的发展，采用CFD方法能够快速地计算流体性能。另外，CFD方法仅能计算有限个攻角时拖缆的阻力性能，为了得到实际不同攻角的速度，需要采用三次样条插值的方法来插值求得。

1 流体力学基础理论

1.1 控制方程

不可压缩粘性流体的连续性方程和动量方程为

(1)

(2)

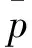
1.2 湍流模型

要使上述方程封闭，须引入新的湍流模型方程，把应力项中的脉动值与时均值联系起来。RNGk-ε方程中湍流动能k和湍流脉动强度ε的输运方程为

(3)

(4)

常数为：G1ε=1.42；G2ε=1.68；Cμ=0.0845；

σk=1.0；σε=1.3；η0=4.38；β=0.012。

2 CFD模拟

2.1 流体计算域

拖缆微元与迎流速度的夹角(即攻角)从0°到90°范围变化。0°及90°情况较为简单，可以较快地得到结构化网格，较为复杂的是0°至90°之间的情况。对于此种情况，将速度入口由平面改为弧形面，可以较好地解决这一问题[4]，其流体计算域及边界设置情况见图1。

需要说明的是，拖缆微元在不同攻角时阻力性能是不同的，而计算时又不可能由CFD的方法计算每种攻角情况，为了解决这一问题，采用三次样条插值的方法[5]。

2.2 网格划分

为了得到高质量的网格，对整个计算域采取分块化处理，再划分为结构化网格。在拖缆周围设置边界层网格，第一层控制近壁面的网格高度和质量，近壁面高度按估算公式(5)确定：

(5)

式中：Δy为第一层边层界厚度；L为长度值；Re为雷诺数。实际取y+为30，整体网格数量为90万个。拖缆流场网格见图2。

2.3 边界条件

边界条件的设定是保证CFD实现的必要条件之一。本文计算域的边界条件设定见图1，包括：速度入口、压力出口、壁面和对称面。

1)速度入口：在进流面设定迎流速度的大小和方向，Vin=V0；

2)压力出口：在出流面设定相对于参考压力点的流体静压力，Pout=0；

3)壁面条件：潜艇表面及圆柱表面设定为不可滑移边界条件，u=v=w=0；

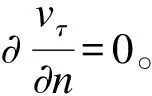
2.4 数值计算

采用有限体积法离散控制方程和湍流模式，并用耦合隐式求解法计算。在差分格式中，压力项使用标准格式，动量项、湍流动能项以及耗散率项先使用一阶迎风格式迭代500次，再采用二阶迎风格式[6]。

采用RNGk-ε湍流模型，并采用有限体积法对控制方程进行离散。压力-速度耦合迭代求解采用协调一致的SIMPLEC算法，压力项采用标准离散格式外，动量、湍流动能和湍流耗散率采用二阶迎风格式，亚松弛因子均采用默认值。近壁处区域采用壁面函数法[7]。

3 三次样条插值

在实际计算过程中，通过CFD方法计算拖缆微元在攻角分别为0°、10°、20°、…、90°的阻力情况。实际计算时若碰到不同属于上述攻角情况时，采用三次样条插值的方法进行估算[8]。

曲线插值一般有指数函数插值、拉格朗日插值、三次样条插值、B样条曲线、NURBS曲线等方法。这里采用三次样条进行插值。

在区间[a,b]内给定一个分划Δ：a=x0

1)每个子区间[xi-1,xi],i=1,2,…,n上为三次多项式；

2)y(x)在整个区间[a,b]上二阶连续可导。

则称y(x)为区间[a,b]上关于分划Δ的三次样条函数，其中xi(i=0,1,…,n)称为节点。插值点如表1所示。

表1 三次样条曲线插值点

则三次样条插值函数为

(6)

式(6)中：

hk=xk+1-xk(k=0,1,…,n-1)

(7)

λkmk-1+2mk+μkmk+1=gk(k=1,2,…,n-1)

(8)

其中：

4 拖缆计算方法简介

由于拖缆是柔性的，受力将发生变形[8]。因此，各处拖缆的来流攻角是不同的。采用有限差分法，将拖缆处理成有限个小段，对各小段分别受力分析，由初始点的力、转角条件求出未知位置的力、转角及坐标点。

为了满足工程中的需要，且基本满足实际情况，做出以下几点假设：

1)拖缆在张力作用下的伸缩忽略不计；

2)拖缆为柔性的，不传递弯矩；

3)整个流动为二维流动；

4)作用于拖缆微元上的水动力系数等同于作用于无限长的拖缆。

将一小段拖缆微元进行受力分析，见图3。

按照切向力与法向力方向进行分解，由力的平衡可得：

(T+dT)sin(dφ)+pdscos(φ)=Dds

(9)

(T+dT)cos(dφ)=pdssin(φ)+Fds+T

(10)

式 (9)、(10)中：T为拉力；D为单位长度拖缆法线方向的力(由CFD及三次样条插值计算)；F为单位长度拖缆切线方向的力(由CFD及三次样条插值计算)；p为单位长度拖缆在水中重力。

忽略二阶小量，由式(10)得：

(11)

将式(11)代入式(9)得：

(12)

由式(11)、(12)可求出不同位置拖缆拉力、转角等值。

另外：

dx=ds×cosφ

(13)

dy=ds×sinφ

(14)

由式(13)、(14)可求出相应位置点的坐标值。

5 计算结果分析

在实际计算时，可能会遇到不同直径的拖缆。众所周知，在CFD计算中，最为复杂的是采用ICEM来划分结构化网格，耗费了大量的人力、物力。目前，Workbench(15.0版)后已经将ICEM集成进去，但是当修改拖缆直径后，ICEM的拓扑分块处理并不能自动化解决，还是需要大量、重复性人工干预。为了较好地解决这一问题，采用ICEM自带的脚本语言，将划分网格中的建组、分块、划网格、导出网格全过程监控、录制并保存，当模型的直径发生变化时，重新读入一次脚本语言，即可一键化划分网格，将原本需要2 h左右的划分网格时间缩减至1 min以内。需要说明的是，建立模型的直径需要在Workbenchk中的DM模块下进行，建立好模型后，仅修改其直径等参数，以便于脚本语言无缝识别，否则在其它建模环境中，如Pro/E、Rhino等，脚本语言对点、线、面、体的识别极易出错。

以直径为10 mm的拖缆(长度为1 m)为例，其在迎流速度为5 kn，其切向力及法向力见表2。