基于ISIGHT/MATLAB的平衡机参数集成优化设计

杨戬，王敏毅，黄朝学，宋向华

(中国船舶重工集团公司第七一〇研究所，湖北 宜昌 443003)

0 引言

平衡机是多管火箭发射装置的重要组成部分，主要用于平衡起落架相对耳轴产生的重力矩。传统式平衡机[1]中的弹性元件由扭簧构成，当刚度确定之后，其产生的重力矩只与起落架的俯仰角有关。对于多管火箭发射装置而言，空载状态和满载状态下的重力矩数值相差较大，在设计平衡机时取空载工况和满载工况的中间值作为平衡目标，导致发射装置剩余的最大不平衡力矩仍然较大。为此，某设计人员提出了主动式平衡机[2]的设计思路。

主动式平衡机在传统式平衡机的设计基础上，将平衡机的刚度设计为可调的，即在不同的装弹模式下，可以调整相应的平衡机刚度与之适应，从而将发射装置剩余的最大不平衡力矩减少了59.4%。通过对主动式平衡机和发射装置的深入研究之后，发现剩余的最大不平衡力矩仍可以进一步减小。本文拟采用MATLAB软件对主动式平衡机和发射装置进行优化设计，使两者间的适配性达到最佳，从而在最大限度上减少剩余的最大不平衡力矩。

1 模型建立

1.1 起落架重力矩

某24管火箭发射装置的俯仰范围为0～75°，装载A、B两种弹，其中A弹18枚，每枚40 kg；B弹6枚，每枚75 kg。为了保证发射装置整体重心位置尽可能的低，规定较重的B弹装载在最下面一层定向器中[3]。

起落架重心和耳轴的相对位置如图1所示，起落架重心到耳轴的距离为L，由于弹的种类、弹的数量和弹的位置都是可以任意变动的，重心位置、起落架质量和距离L都会发生改变。图1为起落架的侧向视图，以起落架尾部为原点建立坐标系。

设重心坐标为G(xG,yG)，则空载情况下的重心坐标为G0(x0,y0)，耳轴中心位置坐标为Oe(xe,ye)，第1、2、3层炮管中分别装载A弹i,j,k枚，B弹装载在第1层，为q枚，且弹的质心在定向器中心轴线上，则重心的坐标可以表示为

(1)

(2)

式中：mA,mB为A,B弹的质量；xA,xB为A,B弹质心相对坐标系中x轴的位置坐标；h1,h2,h3为第1、2、3层定向器中心轴线到x轴的距离。

则重力矩函数可写为

M(θ)=L·mg·cos(α+θ),(0≤θ≤75)

(3)

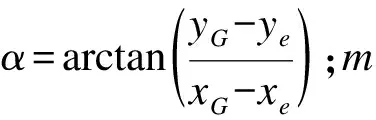
1.2 平衡力矩

主动式平衡机选取每种装弹模式下的最大重力矩值为平衡目标，则平衡力矩为

T(θ)=K·(θ-37.5),(0≤θ≤75)

(4)

式中K为不同装弹模式对应的平衡机刚度值。

2 问题描述

某装弹模式下的起落架重力矩曲线和主动式平衡机输出的平衡力矩曲线如图2所示。

随着俯仰角的增大，起落架相对耳轴轴心产生的重力矩会由正变负，将重力矩为零时对应的俯仰角称为重力矩零点。同样的，平衡机中的扭簧需要进行2个方向的扭转来产生平衡力矩，为了保证扭簧工作可靠性，规定扭簧双向等幅度扭转[4]，则俯仰角为37.5°时为平衡力矩零点。

通过对力矩曲线的分析可知，导致主动式平衡机和发射装置间适配不佳的原因主要有：

1) 重力矩零点偏离平衡力矩零点较远；

2) 设计每种装弹模式对应的平衡机刚度时没有取最优值。

3 优化设计目标模型

3.1 重力矩零点优化

通过对重力矩函数的分析，在装弹模式和俯仰角不变的前提下，重力矩零点只与耳轴位置有关，即以耳轴位置(xe,ye)为设计变量。

不同装弹模式对应的重力矩零点不同，但都分布在一个重力矩零点区间内，通过分析，该区间的中点与平衡力矩零点重合时可以达到最优，即优化目标就是使该中点向平衡力矩零点靠近。以某装弹模式为例，根据式(1)-(3)，该装弹模式下的起落架重心位置为G(xG,yG)，则其重力矩零点为

不同的耳轴位置，对应不同的重力矩零点区间，建立耳轴位置坐标和重力矩零点区间中点的函数关系，则优化目标函数可写为

(5)

其约束条件主要是空间约束[5]：

1)设计变量上下限。根据发射装置总体布局要求，则有：

xmin≤xe≤xmax,ymin≤ye≤ymax

2)重心位置约束。在俯仰运动全过程中，要求重心位置不低于1 400 mm，即：

yGmin≥1 400

综上可知，耳轴位置优化是一个带约束的二维非线性规划问题。

3.2 平衡机刚度值优化

完成对耳轴位置优化之后，需要对每种装弹模式对应的平衡机刚度进行优化，使每种装弹模式下剩余的最大不平衡力矩最小。

以空载工况为研究对象，该装弹模式下剩余的不平衡力矩函数可写为

ΔM(θ)=|M0(θ)+K(θ-37.5)|

(6)

即求对应的K值使剩余的最大不平衡力矩最小。

4 基于ISIGHT的优化设计

4.1 优化流程设计

本文采用ISIGHT作为优化软件[6-8]，一是ISIGHT提供了较为完备的优化算法，其次是利于在之后的优化过程中整合有限元等分析软件，对模型的优化进行多方面的仿真验证。针对耳轴的位置优化和平衡机刚度值优化的问题，利用ISIGHT集成MATLAB组件进行优化计算。首先采用ISIGHT中的二次规划算法(NLPQL)对耳轴位置进行优化，然后将优化后的耳轴坐标作为输入值输入MATLAB程序中，完成对平衡机刚度值的优化。

4.2 优化结果分析

ISIGHT中对耳轴位置坐标以及优化目标函数的迭代过程如图4所示，最终得到的优化结果为(-200，338)。

得到了新的耳轴位置后，即对每种装弹模式对应的平衡机刚度值进行优化。优化前，设计者以俯仰角为0时的重力矩作为平衡机的平衡目标，虽然此时的剩余不平衡力矩接近0，但是随着俯仰角的增大，剩余的不平衡力矩会越来越大，并且在俯仰角为75°时达到最大。为此，需要选择合适的K值使整个俯仰范围内剩余的最大不平衡力矩最小。

根据式(6)编写MATLAB优化程序， 将新的耳轴位置坐标输入优化程序中，得到每种装弹模式对应的最优刚度值，此时某装弹模式下的起落架重力矩曲线和主动式平衡机输出的平衡力矩曲线如图5所示。

优化前后发射装置满载、半载和空载工况下剩余的最大不平衡力矩如表1和表2所示。

通过优化前后的对比，优化后的剩余最大不平衡力矩大幅度降低，较大地改善了发射时的工况。

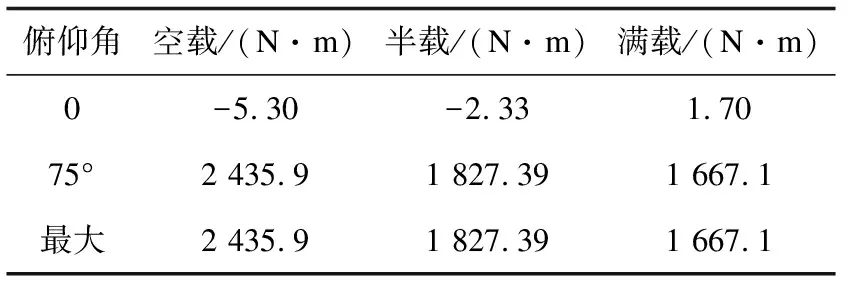
表1 优化前的力矩

表2 优化后的力矩

5 结束语

针对主动式平衡机和某多管火箭发射装置间的适配性不佳的问题，提出了合适的优化方案，并通过ISIGHT/MATLAB的集成优化算法，实现了在最大程度上减少发射装置的剩余最大不平衡力矩的目标。本次优化是建立在数学模型优化基础上的，后期仍可以集成其它仿真软件对优化结果进行实时验证，不过优化过程中的参数设置和其他相关设置还有待进一步的研究和讨论。