铁路客运产品票价的需求弹性分析

杨建国，四兵锋

（1.中国铁路总公司 运输统筹监督局，北京 100844；2.北京交通大学 交通运输学院，北京 100044)

0 引言

近年来，我国铁路经历高速发展阶段，以高速铁路为代表的新兴客运方式已经成为旅客出行的主要选择。据统计，2017年我国铁路旅客发送量30.39亿人次，其中动车组旅客发送量17.2亿人次，占发送总量的56.4%。我国铁路市场化进程也在不断推进，2016年1月，国家对高速铁路动车组票价放松管制。建立现代化的综合客运体系需要充分发挥市场对需求的导向作用，根据各种运输方式的技术经济特点优化市场结构。运价是铁路发展的重要内容，研究多种铁路客运产品下客运需求－票价弹性对我国铁路客运市场化发展具有重要意义。

很多学者对铁路票价问题进行了深入研究，取得了广泛成果。例如，陈建华等[1]分析了不同运输方式服务质量的变化对铁路客运需求的影响，构建了基于弹性需求的铁路客票价格优化模型；四兵锋等[2]综合考虑铁路客运企业和旅客两方面的效益，以运价为决策变量，采用双层规划方法研究了综合运输条件下的铁路客运市场优化问题；张岚等[3]综合运用方式分担模型和层次分析方法，建立铁路客运浮动定价模型，并以京沪高速铁路为例分析了铁路公司的效益随票价变化的情况；刘玉敬[4]构建了市场细分下的不同类型旅客的广义出行费用，提出基于旅客选择行为的高速铁路客票定价模型；程谦[5]以沪宁城际铁路为研究对象，以铁路客运日收益率为决策目标，运用双层规划模型对城际动车组列车票价进行了优化；雷蕾等[6]建立了以运输企业效益最大化、旅客出行费用最小化为目标的双层规划模型，并以北京至上海高速铁路票价为例进行实证分析。

在客运市场中，票价对于客运需求起重要作用。假定其他因素不变，如果某种客运方式的票价上升，其客流就会转移到其他方式上；相反，如果票价下降，那么就会吸引其他方式的客流。显然，铁路客运需求和票价直接影响铁路客运企业的效益。在经济学理论中，需求弹性是指需求对价格的敏感程度，它表明供求对价格变动的依存关系，反映价格变动所引起的供求的相应变动率。目前，关于交通票价弹性的研究主要集中在城市公交方面。例如，Johan[7]采用统计回归分析方法解释了以前研究中对弹性估计的偏差问题，同时，给出美国部分城市公交出行需求对票价的弹性；David[8]评估了在美国城市中地理、人口、票价和公交供给量对人均公交乘坐率的影响，得到了相对较高的公交系统价格弹性；陈伯阳等[9]基于实际数据，研究了城市公交票制票价对公交客运需求的影响机制，分析了在不同条件下的公交需求，以及公交价格需求弹性的变化规律。近期，有些学者对高速铁路的客运需求进行弹性分析，如李文君等[10]将经济学的需求弹性理论应用到高速铁路运输需求分析中，采用实际运营数据对影响客运需求的居民收入、列车旅行速度、高速铁路票价等因素进行了弹性分析及实际测算。

在此，基于旅客的出行选择行为和用户平衡原理，分析铁路客运需求在不同客运产品之间的分离关系，构造数学优化模型求解满足用户平衡的铁路客运需求，采用经济学的需求弹性分析方法描述铁路客运需求与票价之间的变化关系。最后，通过实际数据对模型和计算方法进行说明和分析。

1 多种铁路客运产品下的需求分析

目前，我国铁路已形成包括高速、动车、直达、特快、普快等多种客运产品，不同客运产品所采用的技术手段、运输工具和组织形式不完全相同，其服务质量(包括时间、价格、安全、舒适性等)有很大差别。影响客运需求的因素有很多，除了经济社会等宏观因素外，最为关键的因素就是各种客运产品的服务质量。实际上，客运需求是由各类出行者进行产品选择所形成的聚集结果。因此，分析旅客在出行中的产品选择行为构成了铁路客运需求分析的核心和基础。

首先，假定共有N种铁路客运产品供旅客选择，铁路客运总需求Q保持不变，用qn表示第n种客运产品的需求量，显然，铁路客运需求满足以下条件

在交通研究中，通常采用广义费用来分析出行者选择行为。根据消费者行为理论，旅客总会选择出行费用最小的客运方式。在铁路客运市场中，假定一开始旅客都选择某一种客运产品(比如特快列车，假定一开始它的费用是最低的)。那么随着该产品客流需求的增加，其出行费用就会上升，如排队时间延长、舒适度下降等。这样，就会使得一部分旅客选择其他客运产品，而其他客运产品的出行费用也会随着其客流需求的增加而上升。最终，铁路客运需求会在不同的客运产品之间达到一种平衡状态，这种状态被称为用户平衡状态，可用以下公式来描述这种平衡状态。

式中：GCn为客运产品n的广义出行费用；Cmin为平衡状态下的最小费用。

如果在出行广义费用中考虑拥挤、时间和票价等因素，则可以把出行广义费用表示为一个以客运需求为自变量的单调递增函数。在此，采用以下形式的对数函数形式。

式中：Tn和Pn分别表示第n种客运产品的平均行程时间和平均票价；α和β为待定参数，可以从实际数据中统计估计出来。

可以构造以下的优化模型来描述多种铁路客运产品下的需求分离问题，通过求解该模型就可以得到均衡条件下的各种客运产品的需求量。

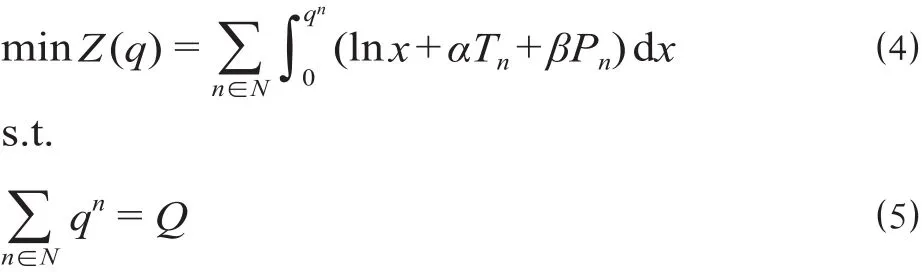
式中：Z (q)为目标函数；q为qn的向量形式。

通过推导上述模型的一阶必要条件，可以证明在均衡条件下，不同铁路客运产品的需求量满足以下的Logit分离关系[9]

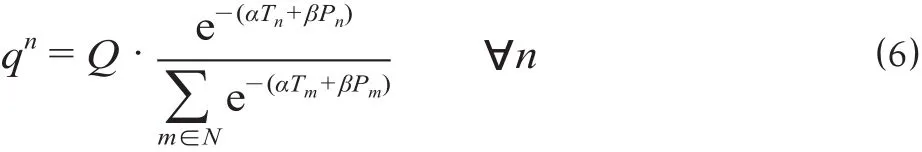
2 铁路客运需求的弹性计算

根据市场规律，铁路不同客运产品的需求量与其票价成反比。也就是说，在其他条件不变的情况下，如果某种客运产品提高票价，则选择该产品的旅客需求就会降低。根据经济学中需求－价格弹性的定义，在票价为Pn*时的铁路客运需求弹性可以表示为

显然，计算铁路客运需求弹性的关键是找到需求对票价的导数。在前面给出的铁路客运需求分离模型中，票价为出行费用中的一个参量，当票价变化时，不同客运产品的广义出行费用就会随之改变，从而导致总需求在不同产品之间的分离关系发生变化。在此，将灵敏度分析方法应用到需求弹性计算上，可以求出平衡条件下客运需求对不同产品票价的导数。

首先，假定其他因素不变，将票价Pn作为上面优化模型的扰动参数。在给定铁路旅客票价Pn=时，采用方向搜索方法(如Frank-Wolfe算法)求解上面的优化问题，得到模型的最优解为此时，该问题在时最优解的一阶必要条件可以写为[10]

设 y = [q (Pn)，μ (Pn)]T，用 Jy表示公式 ⑻ 和公式 ⑼ 对于 [q，μ]的 Jacobian矩阵，用 JPn表示公式 ⑻ 和公式 ⑼ 对扰动参数 Pn的 Jacobian 矩阵 。根据文献[11]，可以得出

根据公式 ⑽，可以得到不同铁路客运产品需求量对旅客票价的导数关系，即∂qn/ ∂Pn*。根据客运需求弹性的定义 ⑺，就可以计算出在均衡条件下的不同客运产品需求弹性En。

3 实例分析

3.1 基础数据

用一个实际例子来说明所提出的模型及算法的应用，所用到的数据来源于中国铁路北京局集团有限公司2017年统计报告。北京到天津之间的铁路客运产品主要有5种，分别为：C字头列车、D字头列车、G字头列车、KTZ字头列车和数字字头列车。为描述方便，将上述5种铁路客运产品分别用数字1～5来表示。2017年北京到天津日均发送客流量为45 128人次，即模型中Q = 45 128人次。北京—天津不同铁路客运产品的分担率及客运需求量如表1所示，北京—天津不同铁路客运产品的平均时耗和平均票价如表2所示。

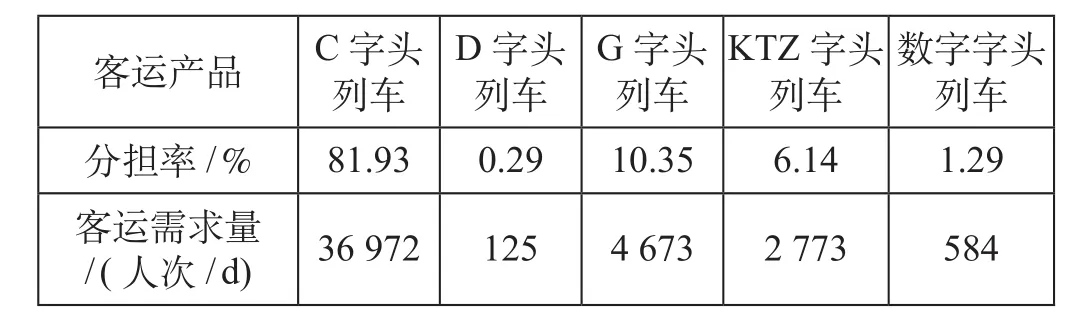
表1 北京—天津不同铁路客运产品的分担率及客运需求量Tab.1 The mode splits and demands of different modes between Beijing and Tianjin

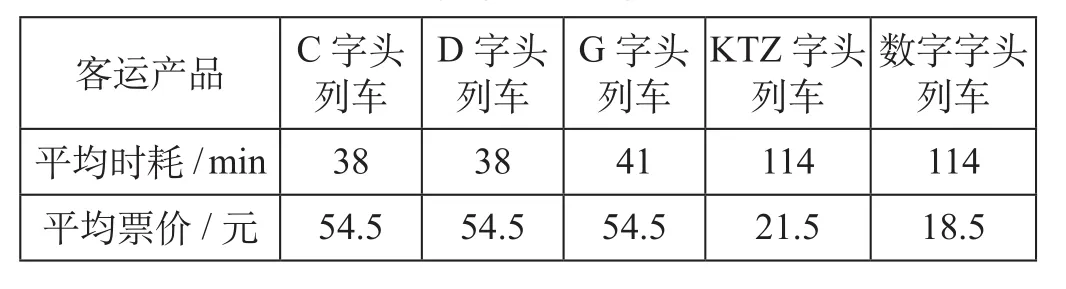
表2 北京—天津不同铁路客运产品的平均时耗和平均票价Tab.2 The average travel times and costs of different modes between Beijing and Tianjin

3.2 参数估计

根据前面的分析，在多种铁路客运产品条件下，如果旅客的出行费用只考虑时间和票价这2个因素，则在系统达到均衡时，不同铁路客运产品的需求分离满足公式 ⑹ 给出的Logit关系。这样，任取一个qn和qm，则有

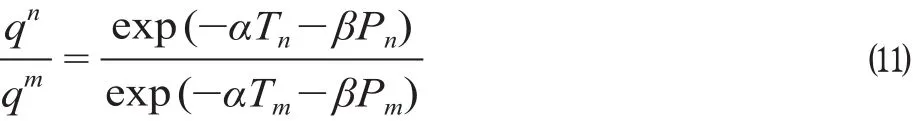
对上式两边取对数，有

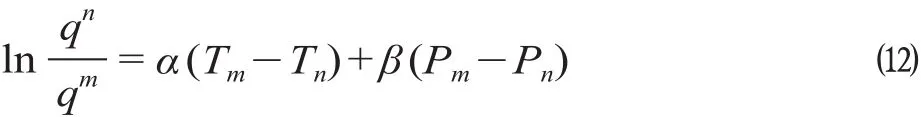
显然，公式 ⑿ 即为所需的线性回归方程。根据多元线性回归方法，采用SPSS软件可以对参数α和β进行估计。参数估计值如表3所示。

3.3 铁路客运需求弹性计算

首先，根据以上基本数据，以及参数α和β的值，求解下层需求均衡模型得到各铁路客运产品的均衡需求。根据前述分析方法，可以得到Jacobin矩阵Jy(p)和Jp(p)。

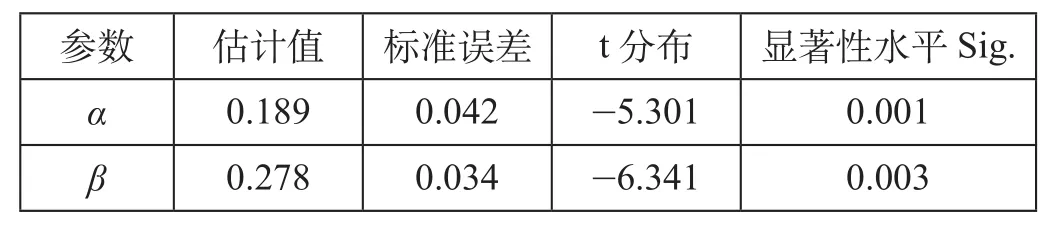
表3 参数估计值Tab.3 The estimations of parameters

将各铁路客运产品均衡需求代入矩阵Jy(p)，产生可得到

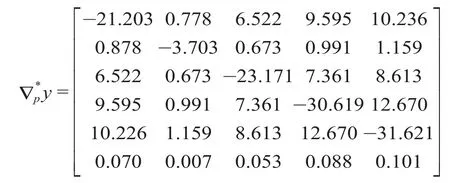
从以上矩阵中可以得出不同铁路客运产品的客运需求对票价的偏导数，进而根据需求弹性的定义 ⑺，即可得出不同铁路客运产品之间的需求-价格弹性。各铁路客运产品之间的需求弹性值如表4所示。

3.4 需求弹性的灵敏度分析

3.4.1 参数 α值对需求弹性的影响

参数α可以理解为旅客的时间价值，α值越大，说明旅客时间价值越高，即旅客越看重时间因素。参数α对各铁路客运产品需求及弹性的影响如图1所示。从图1可以看出，当α增大时，G字头列车的需求会不断上升，而其他铁路客运产品的需求会下降，同时G字头列车对KTZ字头列车的交叉弹性会明显提高，而其他铁路客运产品间的交叉弹性变化不是很明显。

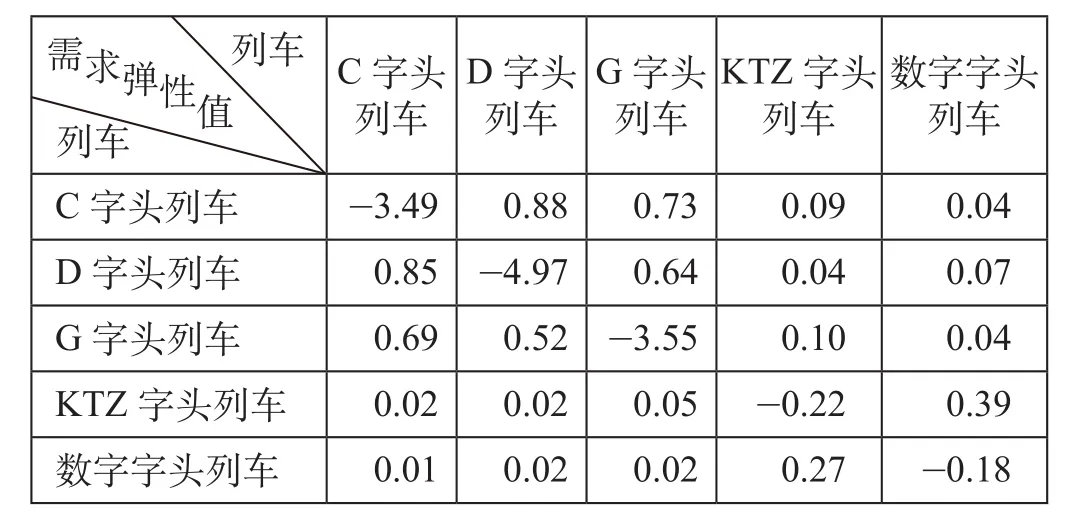
表4 不同铁路客运产品之间的需求弹性值Tab.4 The demand-price elasticities between different modes

3.4.2 β值对公交需求弹性和需求量的影响

参数β可理解为旅客对票价的敏感程度，β值越大，说明旅客越关注价格。参数β对不同铁路客运产品需求量及弹性值的影响如图2所示。可以看出，当β不断增大时，G字头列车需求会快速下降，而票价较低的客运产品的需求会相应上升；同时，G字头列车对KTZ列车的交叉弹性明显下降，而其他产品间的交叉弹性都会上升。

4 结束语

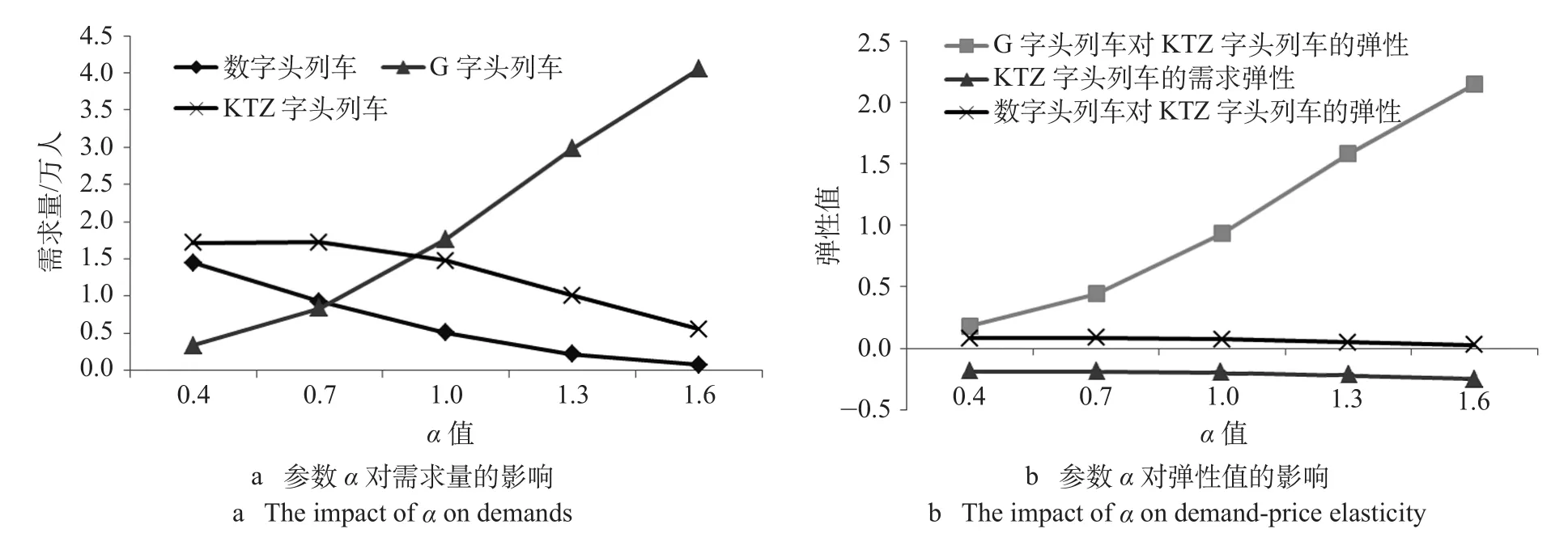
图1 参数α对不同铁路客运产品需求量及弹性值的影响Fig. 1 The impact of α on demand-price elasticity and demands

图2 参数β对不同铁路客运产品需求量及弹性值的影响Fig.2 The impact of β on demand-price elasticity and demands

在市场经济环境下，票价是铁路客运提高竞争力的重要手段，票价体系也是一个国家铁路运输市场化程度的重要标志。改变铁路客运原有定价方式，根据不同细分市场旅客需求弹性建立多级运价体系，是增加运营收入、调节市场需求的有效价格管理策略。目前，我国铁路客运定价机制还没有完全市场化，而在实际中，铁路客运市场会受到诸多不确定性因素的影响，因此，铁路客运定价是一个复杂的政府决策过程。研究构造了数学优化模型来求解满足用户平衡的铁路客运需求，采用经济学需求弹性分析方法描述了铁路客运需求与票价之间的变化关系，通过实际数据对模型和算法进行了验证和分析。在今后的研究中，所提出的方法在以下方面仍需进一步完善：应充分考虑不同类型旅客在出行方式选择上的不同，针对不同类型的旅客，提出基于多类别的铁路客运需求弹性分析；在旅客的广义出行费用中只考虑了时间和票价2个因素，没有考虑舒适性因素，也没有考虑广义费用的随机性问题，下一步应考虑这些因素，使得模型更符合实际；所建立的模型只适合于铁路客运总需求是给定的条件，如何将铁路客运需求作为弹性变量，构造基于弹性需求的铁路客运需求模型及弹性计算方法，也是将来应进行的研究工作之一。