高速铁路动卧列车动态票价的探讨

杨松尧

（辽宁铁道职业技术学院 铁道运输系，辽宁 锦州 121000)

0 引言

截至2017年底，我国高速铁路营业里程达到2.5万km。至2020年，我国将有超过113个大城市开通高速铁路。为了满足旅客需要，2015年1月1日起，开始在北京、上海至广州、深圳间增开高速铁路动卧列车[1]。高速铁路动卧列车属于新兴的客运产品，国内专家学者围绕高速铁路动卧列车运营中的开行方案[2]、票价机制等问题一直在进行研究探索。铁路运输费用市场化一直是一个难题[3]，在高速铁路动卧列车票价市场化方面，国内学者研究较多。安仲文[4]就高速铁路动卧列车市场化定价进行分析，并提出市场化方案设计。张天伟等[5]就高速铁路夕发朝至旅客列车需求进行研究，从直接费用、时间损失、疲劳恢复等角度进行探讨，分析了5种运输产品的优势区间。张红亮等[6]研究了高速铁路与航空竞争条件下长距离客运专线列车票价制定。

动态调整票价应对市场竞争是高速铁路市场化的必然趋势。目前我国高速铁路动卧列车采取淡旺季差异化的定价策略，这种定价策略在一定程度上依据市场的供求关系对票价做出了调整，但是没有完全实现市场化。为此，将高速铁路二等座、高速铁路动卧、航空3种出行方式进行比较，根据客流特征制定高速铁路动卧定价策略方案，利用大站票额预测理论建立双层规划模型[7]，依据市场规律制定合理票价。

1 高速铁路动卧列车票价双层规划模型构建

1.1 模型构建

高速铁路动卧列车票价问题可以看作是一个有2个决策者的双层规划问题，其中决策者为高速铁路运营单位和旅客。高速铁路运营单位可以通过调整票价或改善运输服务质量来影响旅客选择交通方式。旅客通过对交通方式的比较，选择适合自身的交通方式。

铁路运输企业承担一定的社会公共运输责任，从高速铁路运营单位的角度考虑，其目的是在政府定价体系下追求最大的经济效益。因此，高速铁路动卧票价应在人均运输成本和政府限制最高价格之间波动。

上层规划模型如下。

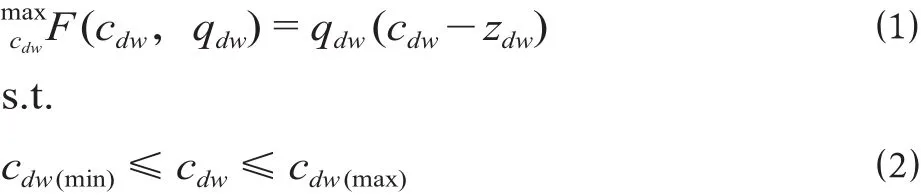
式中：F (cdw，qdw)为铁路运输企业开行动卧列车的运输收益；cdw为OD间动卧列车的票价；qdw为OD间动卧列车的客流；zdw为人均公里可变成本；cdw(min)为由运行成本控制的最低票价；cdw(max)为由政策决定的最高票价。

下层规划模型是一个交通流分配模型，模型中的交通流分配按照高速铁路二等座、高速铁路动卧及航空的影响力采取均衡配流模型。旅客出行时广义费用值最低。

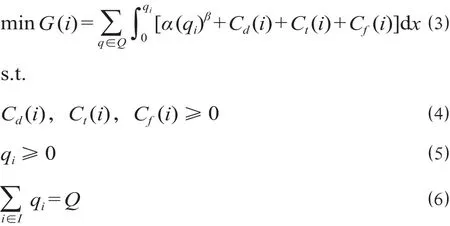
式中：G (i)表示旅客选择第i种出行方式费用总和最低；qi为第 i种交通方式的客流量；α，β为待定参数；α (qi)β表示客流量为qi时，对旅客出行费用的影响；出行费用Cd(i)，Ct(i)，Cf(i)为非负值；Q为客流总量 ；I为出行方式总数。

旅客出行是一个双向选择的过程。旅客总是希望选择广义出行费用最低的交通工具，而运输企业则寻求收益最大化。旅客出行方式的选择会影响广义出行费用和企业的运营成本，最后又反作用于旅客，最后达到客流分配的平衡。在市场经济条件下，旅客运输可以认为是一种消费行为，旅客货币成本、时间成本是决定客座率的主要因素。旅客出行广义费用指旅客向运输企业花费一定的货币和时间来实现旅客的空间位移。因此，旅客出行由运输费用、运输时间、中转费用、中转时间、旅行疲劳等要素决定。旅客出行的费用函数为

式中：Cd(i)为第i种出行方式的直接费用；Tf(i)为第i种出行方式由出发地车站(机场)到目标地车站(机场)的费用，由运价率和走行公里数决定；Cw(i)为第i种出行方式到达、离开车站(机场)的交通费用，由运价率和走行公里数决定。

式中：Ct(i)为第i种出行方式的时间换算费用； Tt(i)为第i种出行方式由出发地车站(机场)到目标地车站(机场)所消耗的时间；Wt(i)为第i种出行方式到达、离开车站(机场) 所消耗的时间；θ为时间价值。

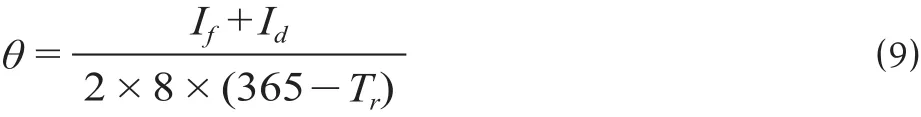
式中：If为出发地旅客年均收入；Id为目的地旅客年均收入； Tr为旅客年均休假时长；假设每个工作日工作时长为8 h。

式中：Cf(i)为第i种出行方式的疲劳换算费用； ε为第i种出行方式疲劳费用系数。

ε可以根据卧铺和座席对旅客产生的疲劳程度不同分开赋值。当选择卧铺时，当选择座席时，其中，Tf(i)，Cf(i)，Tt(i) ，Ct(i) 可以通过市场调查获得。

1.2 模型求解

假设客流各种交通方式中均衡分配，均衡分配交通流方法通常采用基于径路流量的F-W模型算法[8]求解。步骤如下。

步骤1：初始化。将第i种客运方式票价的初值设置为Cd(i)，并且设置迭代次数j = 1。

步骤2：以Cd(i)j作为条件，求解双层规划下层均衡配流情况下的均衡解

步骤3：通过灵敏度分析方法计算出第i种客运方式的客流量近似形式

步骤4：将反应函数的近似形式代入到上层子模型的目标函数中。求解目标函数得到新的最优票价C (i)。

2 案例分析

京广高速铁路(北京南—广州南)全长2 298 km，自2015年1月1日在北京至广州间增开高速铁路动卧夕发朝至列车后，北京至广州间呈现出高速铁路动卧、航空等各种出行方式竞争的局面。因此，确定高速铁路动卧列车的定位，制定与市场相适应的动态价格，对于增强竞争优势至关重要。

2.1 数据分析

（1）票价。通过分析2018年3月携程网数据可知，北京至广州机票全价1 900元，折扣均值6.4，飞行时间3.5 h，到达和离开机场费用平均为200元，消耗时间2 h。高速铁路动卧列车运行时间平均9.5 h，到达和离开高速铁路车站消耗时间1 h。高速铁路二等座票价恒定，高速铁路动卧、航空票价根据客流状况进行调整，折扣范围在0.5 ～ 1之间。

（2）模型参数。根据交通流分配的特性取α = 2，β = 0.8；根据京津冀地区和珠三角地区的平均工资水平，取θ = 41.7 (元/ h)。

（3）客流量。通过调查12306网站和携程网的京广方向日开行高速动车组列车数量、航班数量、动车组列车(航班)定员数，以及2017年上座率信息，可以推算出京广客运通道选择高速铁路二等座、高速铁路动卧、航空3种运输方式出行的旅客日均单向客流约为8 000人。

（4）疲劳度。连续乘车(座席) 4 h以内为轻度疲劳，ε值取1；连续乘车(座席)超过4 h为重度疲劳，ε值取2。

2.2 动态票价分析

借助MATLAB软件，依据高速铁路动卧列车票价双层规划模型及算法进行求解。

（1）步骤1：初始化。将3种客运方式票价的初值设置为高速铁路二等座Cd(1) = 862，高速铁路动卧Cd(2) = 1 290，航空Cd(3) = 1 900，并且置j = 1。

（2）步骤 2：以Cd(1)，Cd(2)，Cd(3)作为条件，求解双层规划下层均衡配流情况下的均衡解q1，q2，q3。

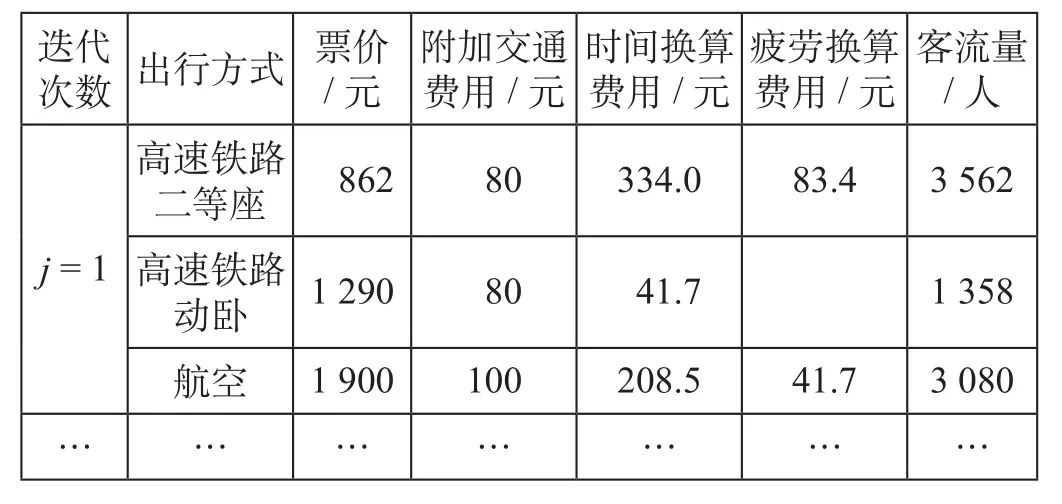
表1 交通费用计算表Tab.1 Traf fi c cost table

（4）步骤4：将反应函数的近似形式代入到上层子模型的目标函数中。求解目标函数得到新的最优票价，高速铁路二等座Cd(1) = 862，高速铁路动卧Cd(2) = 1 246，航空Cd(3) = 1 521。

步骤 5：迭代。设迭代步长 λ为 1。计算 Cd(i)j+1=Cd(i)j+ λ(C (i) - Cd(i)j)，高速铁路二等座 Cd(1) = 862，高速铁路动卧Cd(2) = 1 233，航空Cd(3) = 1 498。

（5）步骤 6 ：利用 |Cd(i)j+1- C (i)|≤ δ 进行收剑判断。取δ= 2，满足条件跳出循环，否则继续迭代。

经过4 538次迭代，在航空票价折扣均值为6.4时，求解出动卧列车最优票价为1 131元，折扣均值为8.7。将计算票价和实际票价相比，比实际票价略低，下浮0.09个百分点。通过该算法求得的票价具有铁路部门和乘客双赢的效果，为高速铁路动卧实行一日一价的票价政策提供研究支持。

3 结束语

高速铁路动卧列车市场化定价是铁路票价改革的全新尝试，也是铁路票价市场化的必然趋势。从市场竞争的角度研究动卧列车票价制定问题，建立符合运输企业的双层规划模型，并设计求解算法。在动态票价实施过程中，应结合中端和高端旅客的比例，对换算费用系数适当调整，使票价在不同的地区对中端、高端旅客有所侧重，从而更好地把握市场；应建立动态票价试点，根据客座率和运输收益对模型参数进行调整和完善。利用定价优势有助于争取离散客流，分摊高速铁路动卧列车固定运输成本，在运输淡季提高客座率。另外，模型中所涉及的一些参数还需要在生产实践中不断完善。