探究一题多解，培养发散思维——谈初中数学发散思维的培养

江苏省扬州市宝应县广洋湖镇中心初级中学 马亚允

创新发展是党的十九大报告中传递出的重要信息，这是未来我国人才发展的一个趋势，也为新时期的教育改革指明了方向。创造性思维是一个人和一个社会智力水平发展到一定高度的“产物”，也是产生更多具有社会意义成果的基石与来源。培养学生创造力和创造性思维成为新时期教育的首要任务，而发散思维则是测定学生是否具有创造力的重要标志，因此借助初中数学的学科优势，着力培养中学生发散思维，值得每个数学教育者关注。笔者在实践中发现，引导学生探究一题多解，对于发散思维的培养，思维灵活性激发以及创造性思维的形成具有积极的推动和促进作用。基于此，本文结合具体的教学案例，对此进行了深入研究和全面解析。

一、探究一题多解，发展发散思维

一个问题只能有一种解法的思维定式，导致了中学生思维僵化，很容易在题型稍加变化的情况下出现无解现象。数学是锻炼学生思维多样化的一门学科，通过探究一题多解，在让学生了解到常规解法之后，引导他们再从不同角度对问题进行审视与，找到更多方法，并从中筛选出最优、最佳方案，是帮助他们提高解题效率，培养中学生聚合思维、发散思维等多种思维共同发展的有效途径。以“多边形内角和”一课为例。

师：三角形内角和为180度，这是我们都了解的，但是四边形呢？大家知道吗？

生1：应该是360度，我们学过的正方形和长方形，它们四个内角都是直角90度，所以内角和是360度。

师：不错，但这两种图形在四边形中是比较特殊的，不具有一般性。想想看怎样将特殊问题转化成一般问题？并由此推测出五边形和六边形的内角和。

这时可以鼓励学生们通过小组合作的形式进行探究，并在讨论之后以小组为代表进行发言。

小组1：四边形可以先连接对角线，使一个四边形变成两个三角形，那么从三角形内角和就可以推导出四边形的内角和。五边形可以以一个点为顶点，向它对应的两个角边接，使一个五边形转化成三个三角形，那么五边形内角和就是3个180度，即540度。

小组2：我们的方法相似，六边形内角和就是先将它分成四个三角形的内角和相加，即720度。

师：不错，大家都找到了一个简单又有效的方法，那么从这个方法中是不是可以将多边形（假设是个n边形）内角和进行归纳？

小组3：通过观察我们通过一个表格进行了归纳。

师：归纳得很到位，那么对于多边形内角和的解法就没有别的方法了吗？

在教师的启发引导下，学生们继续更深层次的挖掘和讨论。

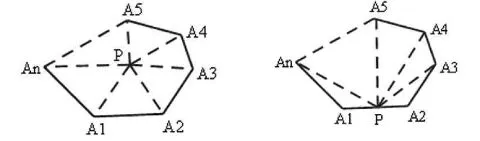
图1

小组4：我们还想到了两种方法，如图1，一种是可以在n边形里取任意点和所有顶点进行连接，就能够得到“180°n-360°=180°（n-2）”。另一种就是在多边形任意边上取一点连接所有顶点，可以得到“180°（n-1）-180°=180°（n-2）”。

二、探究一题多用，碰撞思维火花

发散思维一方面是锻炼学生思维灵活性，让他们的思维不会停留在某个点或者某个面上，而是能够跳出思维定式，多方位和多角度地对问题进行思考、分析和解决，在这个过程中完成思维的创造、创新和发展。另一方面是训练学生思维深刻性，通过“一题多解”和“一题多用”将数学与现实连接起来，让学生通过举一反三，体验数学在解决实际问题时的价值，从而提高对数学的认识。如在探究：“△ABC中，∠ABC的平分线与∠ACB的平分线相交于O点，∠A=40°，求∠BOC的度数是多少？”时，就可以通过一题多用对学生进行思维训练：

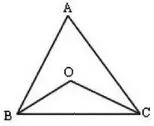
图2

应用①：△ABC中，∠ABC的平分线与∠ACB的平分线相交于O点，∠A=a°，如图2，那么∠BOC的度数是多少？它与∠A之间是否有数量关系存在？

应用②：△ABC中，∠ABC的平分线与∠ACB的平分线相交于O点，∠BOC=a°，那么∠A度数是多少？

应用③：△ABC中，∠BCE和∠CBD两外角平分线相交于O点，∠A=a°，如图3。那么∠BOC度数是多少？它与∠A之间是否有数量关系存在？

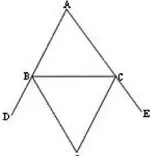
图3

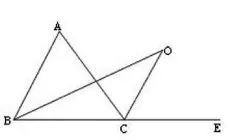
图4

应用④：△ABC中，∠ACE外角平分线与∠ABC的角平分线相交于O点，∠A=a°，如图4。那么∠BOC的度数是多少？它与∠A之间是否有数量关系存在？

结合中学生当前认知能力和水平以及数学思维的递进性和层次性，秉承逐渐深入、逐步递进和环环相扣的原则，设计多种题型进行“一题多用”，体现了数学思维的深刻性和严谨性，让学生们由简到难，由一般至特殊地对题目中隐藏的数学规律进行发现探究，对数学“建模思想”进行了渗透和强化。在这种训练下，学生们的思维越来越灵活，也越来越深刻，完成了知识理论与实践应用的融合和统一。

我国教育无可避免地受到传统教育思想的影响，知识在老师手中一遍遍“填满”学生脑海，而学生则通过不断背诵复习让其成为自己终身记忆，扎实的基础知识反而束缚了学生的思维与思维，让他们失去了创造与创新的机会。教育不应该是填满学生的脑袋，而是要让他们的思维“飞跃”。在初中数学教学中，“一题多解”的模式是对学生思维最好的训练，但同时教育者也应该积极探索更好的方法，让中学生在知识的同化与建构的过程中实现思维的提升与发展。