数形结合思想在高中数学中的灵活应用

江西省赣州市赣县第三中学 温桂花

纵观每年的高考数学试题，不管是选择题、填空题，还是解答题，很多试题的解答都需要利用数形结合的思想。数学结合思想可以说是解答数学问题的一种基本思想方法，对此思想方法的熟悉与掌握，对于学生数学解题水平的提高具有举足轻重的关键作用。下面就数形结合思想在方程与不等式、函数最值、立体几何中的应用进行例举分析。

一、与方程、不等式相关的问题

1.方程的根与参数间的关系

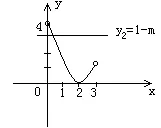
（1）当1-m=0，即m=1时，直线与曲线有唯一交点，则此时原方程有唯一解；

（2）当1≤1-m＜4，即-3＜m≤0时，直线与曲线也是只有一个交点，即原方程有唯一解。

综上分析，实数m的取值范围是-3＜m≤0或m=1。

【评析】注意对数函数定义域的限制。

2.不等式问题

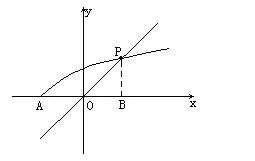
【评析】注意根式函数定义域的限制。

二、与函数相关的问题

1.函数的最值（值域）问题

解析：观察函数的结构形式，可以将原函数看作定点(2,3)与单位圆上的动点(cosx,sinx)的连线的斜率，从而可以将问题就转化为求直线斜率的取值范围问题。在坐标系中画出图形，利用数形结合的方法分析可知，当直线与单位圆相切时，斜率取得最值，且易求得最小值、最大值分别为故原函数的值域为

【评析】数形结合分析函数问题时需要注意分母可能为0的情况，以及最值情况能否取到等问题。

2.函数的单调性问题

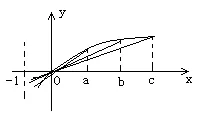
【评析】对于这类具有统一结构形式的式子，多是考虑结合函数图像，借助图像的直观性分析其几何意义。

三、与立体几何相关的问题

例5 假设三棱锥A-BCD的侧面ABC内有一动点P，它到底面BCD的距离与到棱AB的距离相等，那么，动点P的轨迹与△ABC组成的图形可能是（ ）

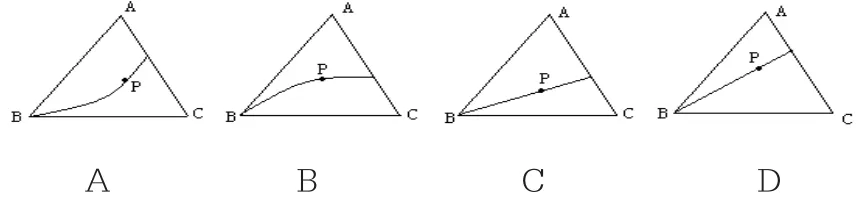
解析：此题是一道典型的几何题目，是立体几何与平面几何的综合问题，这类通过空间与平面相结合考查几何知识的形式是一种常见、热门的考查方式。下面进行分类讨论分析：

（1）若AC⊥平面BCD时，那么如图（1），可以将原问题等价转化为动点P到棱AB的距离和到棱BC的距离相等的点的轨迹，容易判断此时动点P的轨迹显然是∠ABC的平分线。

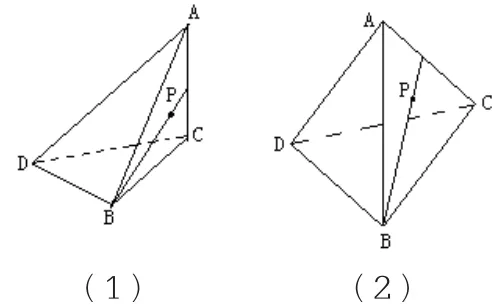
（2）如果AC不垂直平面BCD，那么如图（2），设动点P到平面BCD和的距离为h，到边BC的距离为dBC，二面角A-BC-D的大小为θ，那么有所以选D。

【评析】解决这类空间几何问题，一定要利用空间几何的相关性质，将空间几何问题转化为平面几何问题，然后利用平面几何的有关性质进行求解会相对简单，且不容易出错。

总之，利用数形结合思想，借助于图像来讨论方程的解、不等式的解集、函数的性质、立体几何模型等内容，问题变得简单明了，能让抽象的问题更加直观化，这样有助于学生理解数学问题的本质，强化自身对抽象思维与形象思维之间的转化能力，提升分析数学问题、解决数学问题的能力。