巧妙构造，解决三角类问题

江苏省射阳县第四中学 王 芹

随着新课改的不断深入，出题者对于学生的考查不再局限于简单的解题，而是更多在解题方法上考查。三角类题型作为初中数学中的典型题型，出题者定然下足了功夫，因此，对于学生们来说，就要挖掘其中的解题技巧与解题方法，深入地理解三角形的含义。教师在教学的过程中，要不断地灌输学生正确的思维方法，使得学生在解题的过程中能够养成良好的思路，发散自己的思维，提高解题的效率。

一、中线倍长法

学生们在解题的过程中应该都遇到过中点类的三角形题，这类题有的学生在解题的时候，想着去利用中位线，用其定理，化解难题，但是今天我想告诉学生们的就是在条件或者结论中遇到中点的时候，或者一条线段是另一条线段的二倍时，此时要想到去延长中线的一倍，然后构造出全等三角形，结合条件与结论巧妙地解题。

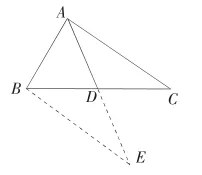
图1

例1 如图1所示，在△ABC中，AB=3，AC=5，试求BC边上的中线AD的取值范围。

解析：根据题意，既然要求BC边上的中线AD的取值范围，学生们可以打开思路，充分利用中点的性质。延长AD到点E，使得AD=DE，连接BE，由题意学生们易证明，于是有EB=AC，由三角形的三边关系可知，BEAB＜AE＜BE+AB，即 5-3＜AE＜5+3，所以有 2＜2AD＜8，可知中线AD的取值范围是AD∈（1,4）。

点拨：本道题中，通过构造了辅助线，将中线AD化解成了ED，然后通过证明三角形的全等，得出AE的范围，利用中点的性质，最后求出中线AD的取值范围。短短的一个三角形类题型，通过巧妙的构造，巧添辅助线，化解了难题，大大节省了学生们的解题时间，提高了正确率，可见，这种解题方法将有利于学生们思维的延伸，因此，学生要牢记中线倍长法，合理地化解三角类题型。

二、截长补短法

截长补短法相信学生们一定耳熟能详，但是学生们要明确用法以及在什么题型下用。当学生们在解题的过程中，遇到题目或者结论中出现一个角是另一个角的二倍，或者一条线段是另外两条线段的和的时候，这时候就需要巧添辅助线，截长补短，构造全等三角形来解决问题。

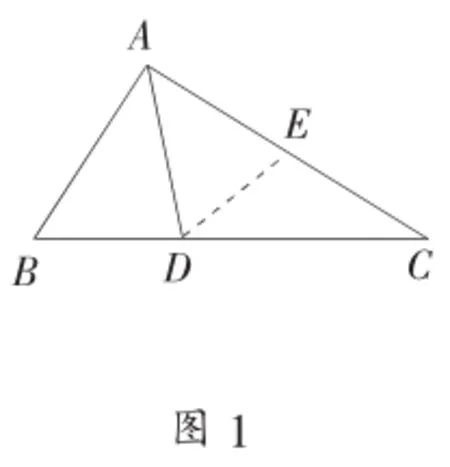
图2

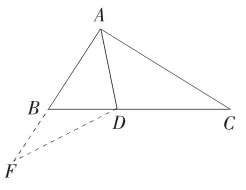
图3

例2 如图所示，已知在△ABC中，∠B=2∠C，AD是∠BAC的平分线，试证明：AC=AB+BD。

解析：此处既然谈到截长补短法，那么我就分开为学生们讲解。首先，运用截长法，如图2所示，在AC上截取AE，使得AE=AB，连接DE。根据题意易知，∠BAD=∠CAD，易证明△ABD≌△AED，于是有BD=DE，∠B=∠AED，又因为∠B=2∠C，所以就有∠AED=∠EDC=∠C，那么有ED=EC，即EC=BD，所以AC=AB+BD。现在给学生们讲解补短法的思路，如图3所示，只需要延长AB到点F，使得AF=AC，连接ED。根据前面的截长法，证法相同，可以证明出AC=AB+BD。

点拨：本道题运用了截长补短的方法，给学生们分别演示了截长与补短的做法，相信学生们肯定深有体会，巧妙地添加辅助线，构造三角形，将问题放到三角形中去解决，提高了解题的效率，长期积累，也可以锻炼学生们的思维能力。

三、巧添平行线

说到几何图形，那么平行线不得不说。平行线可谓是初中数学中的重点，对于解三角形类的题型应用的也比较多。学生们在做题的过程中，遇到题目或者结论中出现线段相等或者遇到角平分线时，这时候发现利用三角形全等貌似很难求解，那么就可以通过添加平行线，构造出一个新的三角形，结合条件与结论求解。

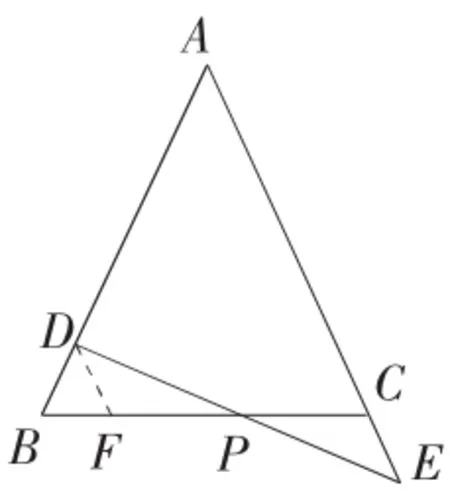
图4

例3 如图4所示，在△ABC中，AB=AC，D为AB上一点，E为AC延长线上一点，且CE=BD，连接DE交BC于点P，求证：PE=PD。

点拨：在几何图形证明题中，巧添平行线是常用的手法之一，学生们在遇到题目或者结论中出现线段相等或者遇到角平分线时，一定要想到添加平行线的方法，将复杂的问题简单化，明确自己的思路，方能又快又好地解题。

总之，在千变万化的数学题中，掌握住方法，掌握住解题技巧，就能发现数学中蕴含的规律所在，巧解难题。在全等三角形这一块，学生们要充分利用所学，加强对解题方法的研究，巧妙构造，理清自己的思路，三角问题也就迎刃而解了。