从一个题浅谈一类不等式题的解题策略

浙江省余姚市第八中学 陈银燕

高考命题重点考查均值不等式和证明不等式的常用方法，单纯不等式的命题，主要出现在选择题或填空题，一般难度不太大。在近年的高考中，不等式的考查有选择题、填空题、解答题，不仅考查不等式的基础知识、基本技能、基本方法，而且还考查了分析问题、解决问题的能力。解答题以函数、不等式、数列、导数相交汇处命题，函数与不等式相结合的题多以导数的处理方式解答，函数不等式相结合的题目，多是先以直觉思维方式定方向，以递推、数学归纳法等方法解决，具有一定的灵活性。在一次联考中，填空题最后一题考查基本不等式。下面就由此题展开，谈谈对于此类不等式的解题策略和思考。

一、考题引入，一题多解

初次看到这一题,脑海中的第一种想法是利用基本不等式。在考试之前,正好在带领学生复习不等式的知识,只是学生中能灵活运用基本不等式的不多,只能解常见题,简单不等式求最值，有个别学生连“一正，二定，三相等”都不能很好理解。以下是对这个题的几种不同解法。

∵ S=xy，x＞0，y＞0，∴ S＞0，

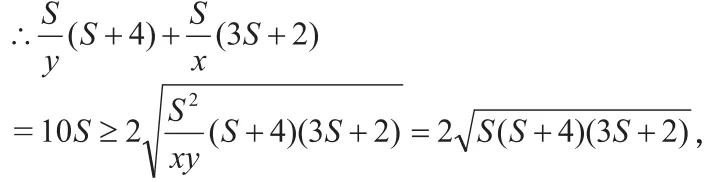
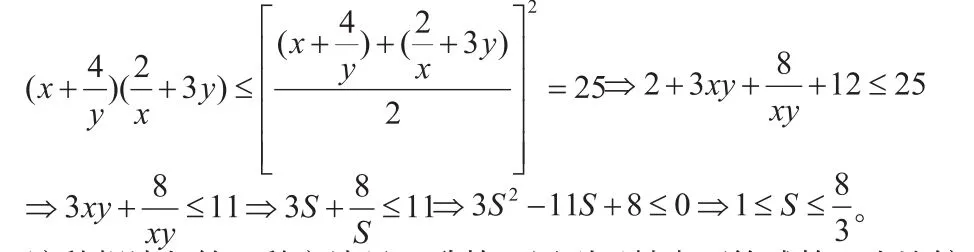
这种想法与第一种方法是一致的，用到了基本不等式的一个比较常用的变形可以很好地把两个数的加法与乘法联系在一起。

其实这题是泰州2015届高三调研(三)卷中14题原题,除了上面两种想法外,还可以用其他的方法进行拆分组合,最大最小值分开来算。(因为此题涉及的是正实数x,y，以下解题不具体说明）

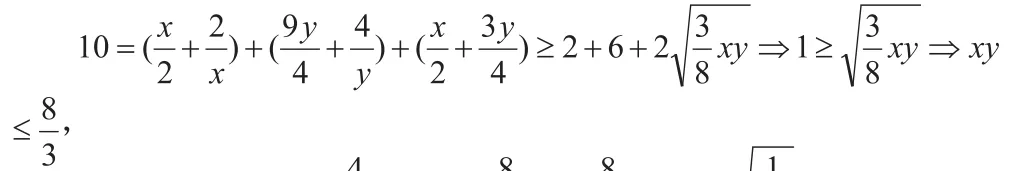
对学生来说,解法三、四很难会想到,解法四对学生不作要求,解法五的想法比较灵活,用函数的思想解决最值问题,前提先消元,视为x的函数，用函数性质来解题。

上述是一题多解,从不同角度来解决不等式求最值问题,这类题比较喜欢放在填空题压轴题的位置,在高考中出现概率非常高,变式题也非常多。

二、考题链接，变式拓展

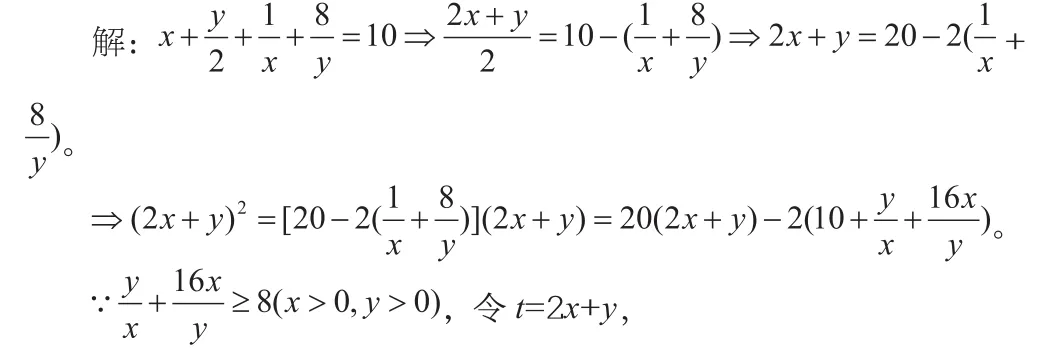
∴t2≤20t-362≤t≤18，当且仅当x=3，y=12时，（2x+y）max=18。

变式三的这种解法是比较典型的，出现2x+y这个整体,用整体的想法,也可以对原题左右同乘2x+y,利用基本不等式把其变为定值。实际上,大多数题目是凑好的，否则在用基本不等式的时候，不等式右边是无理数，题目再做下去就比较麻烦，当然个别题除外（比如可凑成完全平方解答）。

另解：这个题也可以构造“1”,关键是怎么构造。

掌握这两种方法,解温州市2015届高三第一次适应性测试数学第6题,已知正数x,y满足则求x+y的最大值就非常方便了。

以上是对这一类不等式提供的几种解题策略，但具体问题还需具体分析。在复习解不等式过程中，注意培养、强化与提高函数与方程、等价转化、分类讨论、数形结合的数学思想和方法，逐步提升数学素养，提高分析解决综合问题的能力。能根据各类不等式的特点，变形的特殊性，归纳出各类不等式的解法和思路以及具体解法。