基于神经网络的低信噪比CBOC信号组合码序列盲估计

张天骐,张 婷,熊 梅,赵 亮

(重庆邮电大学信号与信息处理重庆市重点实验室,重庆 400065)

0 引 言

随着各国卫星导航技术的不断发展与深入研究,二进制偏移载波(binary offset carrier,BOC)[1]调制技术因其独特且良好的频谱分裂特性被广泛应用于各国导航系统中[2]。为适应日益增长的技术要求,美国与欧洲委员将多元BOC(multiplexed BOC,MBOC)[3-4]调制应用于Galileo 公开服务和全球定位系统(global position system,GPS) ⅢA 民用信号,此时虽制定了MBOC调制信号的功率谱标准,但并未说明信号详细的实现方式。后续发展的过程中,MBOC信号的主要实现形式为时分复用BOC(time multiplexed binary offset carrier,TMBOC)[5]调制以及复合二进制偏移载波 (composite BOC,CBOC)[6]调制两种方式。美国的GPS、欧盟的Galileo卫星导航系统以及中国的“北斗”导航系统中均选择使用了复合二进制偏移载波(composite binary offset carrier,CBOC)调制信号。CBOC信号相对于传统的二进制相移键控(binary phase shift keying,BPSK)信号来说,灵敏度和抗多径性能上有都有一定程度上的改善和提高。因此,对CBOC信号的相关序列特征与参数特征进行深入研究学习具有重大意义。

考虑到目前针对CBOC调制信号的研究文献大多数是跟踪[7-8]和捕获[9]方面,而针对CBOC调制信号的序列估计国内外还没有相关的研究。参考针对直扩信号伪码序列盲估计的研究方法,如文献[10]提出采用自相关搜索法,通过对每个采样点计算测度函数,最终实现伪码序列估计;文献[11-12]提出利用特征值分解和奇异值分解(singular value decomposition,SVD)的方法实现伪码序列的估计;文献[13]提出采用盲源分离以及子空间的方法对信号进行批处理后进一步处理实现伪码序列的盲估计。文献[10-13]中采用的各种算法在进行序列盲估计时不可避免会涉及到相关矩阵R的计算,尤其处于非平稳工作环境下以及序列较长时,都会面临算法复杂度高、收敛速度慢、计算量及存储量大等缺点。基于子空间的方法虽然降低了数据的存储量,但算法复杂度复杂度依旧较高,且算法抗噪声性能较差。文献[14-15]提出极大似然函数(maximum likelihood,ML)和Viterbi这两种算法来实现伪码序列的盲估计,但该文献应用的两种算法无法全局收敛,并且不适用于低信噪比(signal to noise ratio,SNR)的条件下。考虑到神经网络(neural network,NN)可以自适应进行特征值提取和模式识别[16],避免了对相关矩阵R的预计算,不涉及批处理运算,具有算法复杂度低、收敛速度快、效率高以及数据存储量低等优点。因此,利用NN的方法来对信号伪码进行盲提取具有极大的发展前景。

本文采用短码调制信号,即一位信息码由一个周期伪码同步调制,文中不讨论长码调制情况。首先尝试将CBOC调制信号建模成一般直扩信号,将CBOC信号中的伪码序列和副载波序列统一看为一个整体,即为组合码序列。其次采用以两倍信息符号周期长度分段的奇异值分解算法来验证CBOC调制信号的组合码序列盲估计的可行性。最后为解决奇异值分解算法对内存要求过高、复杂度较高的缺点,引入基于Hebbian学习规则的主分量分析NN,最终实现CBOC信号组合码序列的盲估计,为信号信息序列的盲估计奠定基础。

1 CBOC信号模型

CBOC信号是在BOC信号的基础上衍生而来,高频信息的添加使码跟踪性能和抗多径性能大大提高。CBOC具体调制方法为:将BOC(1,1)和BOC(6,1)两种调制信号在时域按照一定的功率比加权求和得到CBOC(6,1,1/11),CBOC调制信号产生框图如图1所示。

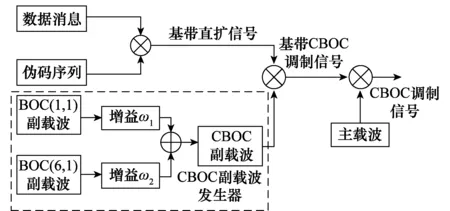
图1 CBOC信号的体制框图Fig.1 Block diagram of CBOC signal

CBOC信号为

SCBOC(t)=A×SCB(t)×cos(2πf0+φ0)=

S(t)×Sc(t)×cos(2πf0+φ0)

(1)

式中,A表示载波信号的幅度;SCB(t)表示基带CBOC信号;Sc(t)表示CBOC副载波;f0表示主载波频率;φ0表示主载波初始相位;S(t)是经伪码序列和信息序列调制产生的基带直扩信号。

CBOC信号与BOC信号最大的区别是副载波的不同,导致信号中被加入高频分量,则信号副载波可表示为

Sc(t)=ω1BOC(1,1)(t)±ω2BOC(6,1)(t)

(2)

式中,ω1、ω2需满足ω1+ω2=1。CBOC信号同时调制数据信号和导航信号,其中数据信号含有导航电文而导频信号不包含。CBOC(6,1,a/b)信号包括数据通道和导航通道,所占的能量比为1∶1。则该信号的表达式可详细表示为

sCBOC+(t)+sCBOC-(t)

(3)

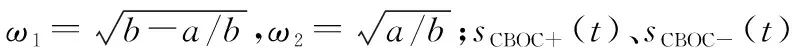
CBOC调制信号存在多种实现方式,具体方式如表1所示。本文所用的实现方式为表1中的第一种调制方式。

表1 CBOC信号调制方式表Table 1 Modulation mode table of CBOC signal

文中以CBOC(6,1,1/11,+)为例,则CBOC(6,1,1/11,+)信号表示为

SCBOC(6,1,1/11)(t)=

(4)

在电子对抗中,获取信号的信息序列为关键所在。因此,尝试将CBOC信号建模成一般的直扩信号,即将信号中的副载波序列和伪码序列相乘并看作一个整体,称这个整体为组合码序列[17]。通过对CBOC信号组合码序列的估计从而达到解扩原信号的目的。如此建模不仅简化CBOC信号序列盲估计问题,同时也为完整获取信息序列奠定基础。图2所示的是CBOC(6,1,1/11,+)信号的组合码序列示意图。

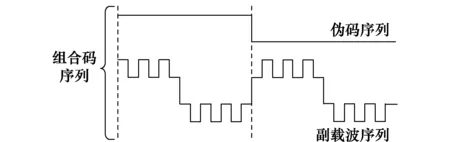
图2 CBOC(6,1,1/11,+)信号组合码序列Fig.2 Combination code sequence of CBOC (6,1,1/11,+) signal

2 基于SVD的CBOC信号组合码序列盲估计

接收到的CBOC信号可表示为

x(t)=s(t-tΔ)+n(t)

(5)

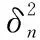
文中采用的间隔为两倍组合码周期2T0,数据重叠T0的时间窗对信号分段,以此得到观测矩阵

X=S+N=[x1x2…xK]

(6)

xk=sk+nk=[xk-1xk-2…xk-2Nc]

(7)

式中,K表示数据组数;X、S、N分别表示接收信号矩阵、有用信号矩阵、噪声矩阵;其中观测矩阵X的维度为2L×K;Nc表示伪码长度。

考虑异步情况,接收端存在时延tΔ,sk的分段起始点和组合码序列的起始点不重合,使得sk中含有3位连续的信息码调制序列,得

sk=dkp1+dk+1p2+dk+2p3

(8)

式中,dk、dk+1、dk+2表示连续的3位信息码;其中p1表示的是长度为L-T0的组合码序列后半部分的波形和长度为L+T0的零值;p2表示的是长度为L的组合码序列波形、以及长度为L-T0和T0的零值;p3表示的是长度为T0的组合码序列前半部分的波形和长度为2L-T0的零值。

由式(8)可推出有用信号矩阵S为

S=[s1s2…sK]=[p1p2p3][d1d2d3]H

(9)

式中,d1=[d1d2dK]T;d2=[d2d3…dK+1]T;d3=[d3d4…dK+2]T。

假设噪声与CBOC信号之间相互独立,则相关矩阵可推得

R=[XXH]

(10)

考虑到实际计算时,式(10)会受到数据向量个数的限制,近似等价为

(11)

当ym各态历经时,有

(12)

(13)

式中,I表示维数为2L的单位矩阵。

设CBOC信号中组合码序列的能量为

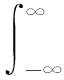
(14)

式中,Ts为副载波码片宽度,将式(14)代入式(13)中,得

(15)

(16)

3 主分量分析NN实现CBOC信号组合码序列盲估计

SVD算法属批处理算法,一般对序列长度有一定限制,并且对计算存储要求高。接下来利用基于Hebbian学习规则的NN算法[18-20]对CBOC信号的组合码序列进行盲估计,NN算法对计算存储量要求合理、计算量小,其结构图如图3所示。

图3所示的模型中输出是输入的线性组合,神经元接收一个含有N个输入信号x1,x2,…,xN的集,其对应的权值分别为w1,w2,…,wN,由图3可将输出y表示为

(17)

为方便表达,设

x(t)=[x1(t),x2(t),…xN(t)]T

(18)

w(t)=[w1(t),w2(t),…wN(t)]T

(19)

式(17)可用内积形式表示为

y(t)=wT(t)x(t)=xT(t)w(t)

(20)

在基于Hebbian学习规则的NN中,网络的权值wi是随训练过程而发生着不断地变化,可提出权值更新公式为

wi(t+1)=wi(t)+ηy(t)[xi(t)-y(t)wi(t)]

(21)

式中,η为步长,令x′(t)=xi(t)-y(t)wi(t),则式(21)简写为

wi(t+1)=wi(t)+ηy(t)x′(t)

(22)

结合式(20)～式(21)可写为

w(t+1)=w(t)+ηy(t)[x(t)-y(t)w(t)]

(23)

由上述公式可画出权值wi的变化流图,如图4所示。

图4描述了式(22)和式(23)之间的关系,图4中z-1为延时算子。因此,将式(20)代入式(23)中有

w(t+1)=w(t)+η[x(t)xT(t)w(t)-

wT(t)x(t)x(t)w(t)w(t)]

(24)

对描述的Hebbian算法,可等价看为最大特征值滤波器,即通过此算法可抽取出输入数据协方差矩阵中最大特征值所对应的特征向量,对算法进行收敛性分析,转化为对式(24)的证明,引入渐进稳定性原理对算法的收敛性进行详细的证明。

证明假设M为足够大的正整数,β为足够小的正常量,存在

(25)

(26)

式(25)中,R=E{xxT},由式(25)、式(26)可知x(k)的变化远快于w(k)的变化。因此,可推导出

w(t+M)-w(t)≈

Mβ[Rw(t)-w(t)wT(t)Rw(t)]

(27)

wT(t)RMw(t)≈wT(t)Rw(t)

(28)

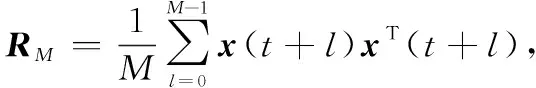
假设当上述两个系统渐进轨迹等价时,可通过对一个系统的收敛性来推断出另一个系统的收敛性。即用{t,t+1,t+2,…}代替式(27)中的{t,t+M,t+2M,…},则

w(t+1)-w(t)=Mβ[Rw(t)-w(t)wT(t)Rw(t)]

(29)

(30)

式中,ei表示自相关矩阵中特征值对应的特征向量;θi(t)表示时变因子,则

θi(t+1)=[1+Mβ(λ-δ(t))]θi(t)

(31)

由文献[19]可知:

已知

(32)

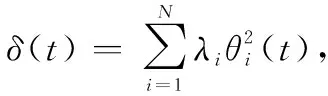
(33)

推导出当t→∞时,存在w(t)→e、δ(t)→λ、δ(t)=wT(t)Rw(t)。

证毕

4 自适应变步长学习算法

在基于Hebbian学习规则的NN中,固定步长存在固有的缺点。当步长取较大值时,会导致算法收敛精度变差甚至不收敛;而步长取较小值时,又不可避免的会带来收敛速度慢的问题。因此,固定步长必然是一个考虑了收敛速度与收敛精度的权衡值,否则一定程度上会造成系统资源浪费。

结合NN自身的学习特性,算法在刚开始学习训练时,由于估计误差较大,此时可选取较大步长以加快收敛速度,但随着NN不断地学习,误差逐渐变小,精度逐渐提高,此时就需要选取较小的步长以防算法出现不收敛现象。因此,为改善算法收敛速度,引入了一种在最小递归二乘(recursive least squares,RLS)意义下的最优变步长模型。

考虑到算法中的权值更新公式含有x(t)-y(t)wi(t)项,令x(t)作为RLS算法中的输入信号,y(t)作为RLS算法中的输出信号,wi(t)作为RLS算法的连接权值,则RLS算法的代价函数为

(34)

式中,0<γ≤1为遗忘因子,其作用是确保在过去某一段时间内的值被遗忘,从而使系统工作于平稳状态。由式(34)可推导出基于RLS算法的权值更新公式为

wi(t)=wi(t-1)+L(t)[x(t)-y(t)wi(t-1)]

(35)

其中

(36)

因此,基于Hebbian学习规则的NN在RLS下的最优变步长学习速率为

(37)

或

(38)

进一步可等效为

(39)

由文献[20]可知,d(0)是一个很小的正数,通过式(39)可知,初始值d(0)与γ值越小,变步长β(k)越大,收敛速度越快。但是当d(0)与γ取值过小(特别当γ过小)时,会导致算法的收敛性不稳定,从而致使收敛速度变慢甚至将无法收敛。

5 算法实现步骤及复杂度分析

5.1 算法步骤

综上所述,基于Hebbbian学习规则下的NN CBOC信号组合码序列盲估计算法步骤简述如下:

步骤1对接收信号进行采样和归一化处理。

步骤2网络初始化,置所有权值wi为均匀分布的1和-1,设置允许的最小误码率(bit error rate,BER)为网络循环的终止条件。

步骤3对于时刻t,输入新的一周期信号数据向量x(t),如果时延不为0则输入三周期信号。

步骤4根据式(20)计算神经元的输出。

步骤5根据式(21)更新NN的权值向量。

步骤6置n=n+1,返回步骤2继续,直到达到允许的最小BER为止。

算法的流程图如图5所示,在本文中终止条件即允许存在的BER设置为e=1%。

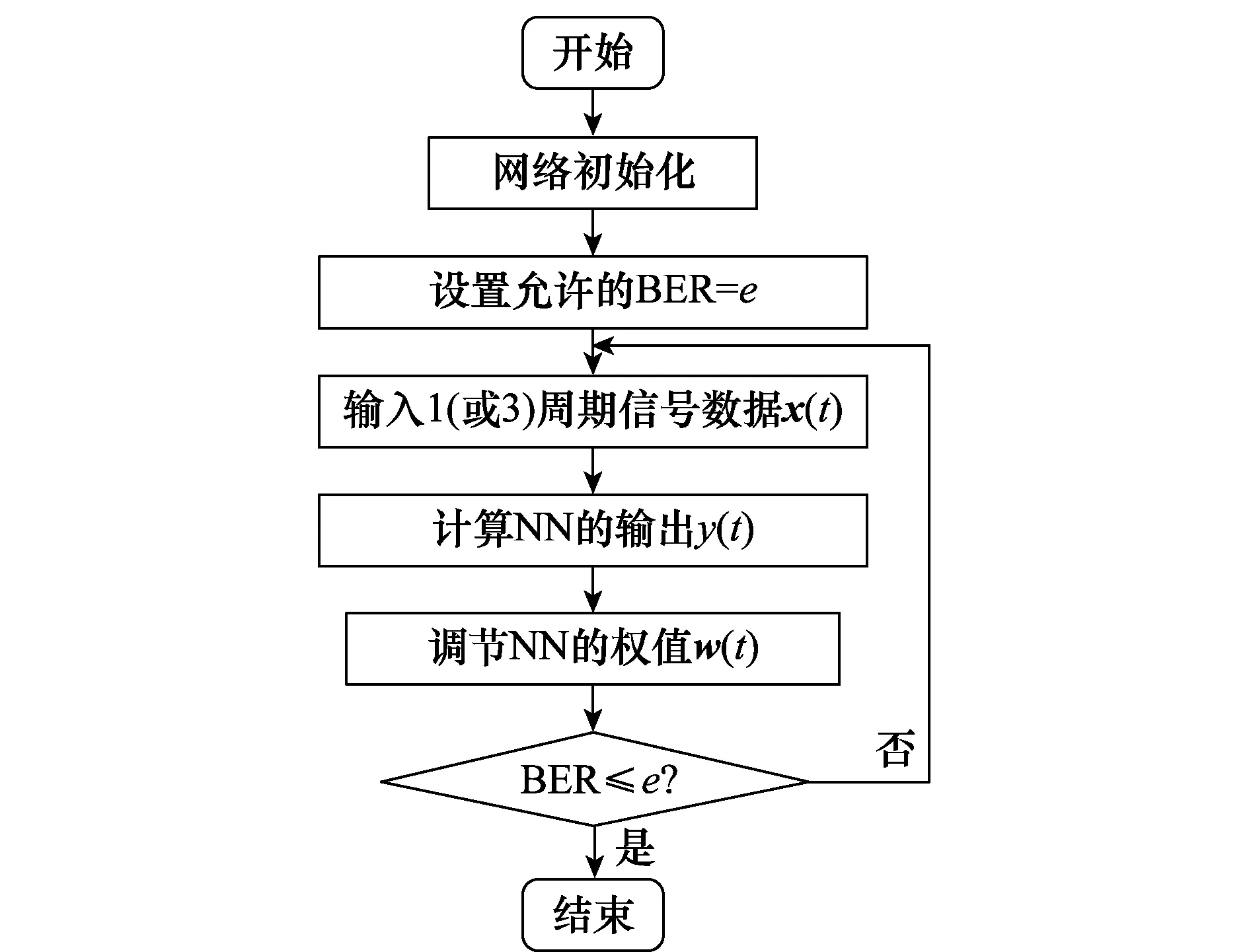
图5 基于Hebbian学习规则的NN流程图Fig.5 NN flow chart based on Hebbian learning rules

5.2 复杂度分析

算法的复杂度是指算法实现过程中所用的乘法次数和加法次数,假设信号组合码序列长度为N,算法达到收敛时所需的数据组数为M,计算算法中单次蒙特卡罗实现下算法所需的复杂度,SVD、自相关搜索算法、本文算法复杂度对比结果如表2所示。

表2 复杂度分析Table 2 Complexity analysis

由表2知,自相关搜索算法和奇异值分解分解算法复杂度远大于本文算法。NN算法作为特征值分解算法的快速算法,避免了批处理中对相关矩阵R的预计算,算法复杂度得以降低,因此,算法复杂度远低于另外两种算法。降低算法的复杂度不仅提高了算法的效率,而且令长序列工作环境下序列估计的可行性大大提高。

6 仿真实验及分析

6.1 实验1

验证SVD算法的可行性,进行如下仿真。实验参数设置为:伪码速率为Rc=1.023 MHz,副载波速率Rs=1.023 MHz,伪码长度L=63,副载波长度为8,即组合码长度为504,SNR=-10 dB,仿真如图6～图10所示。

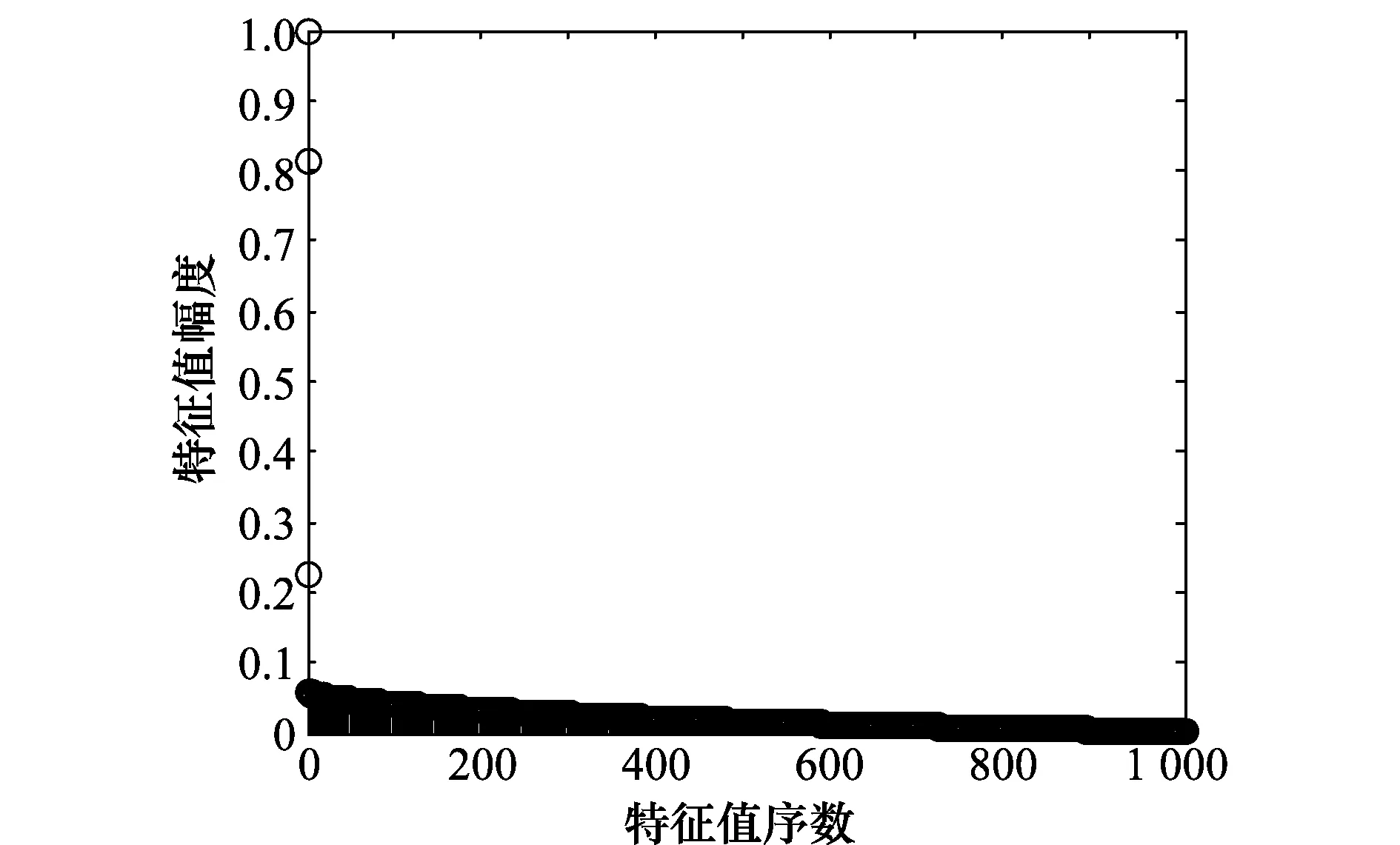
图6 矩阵R1对应的左奇异值谱图Fig.6 Left singular value spectra of matrix R1

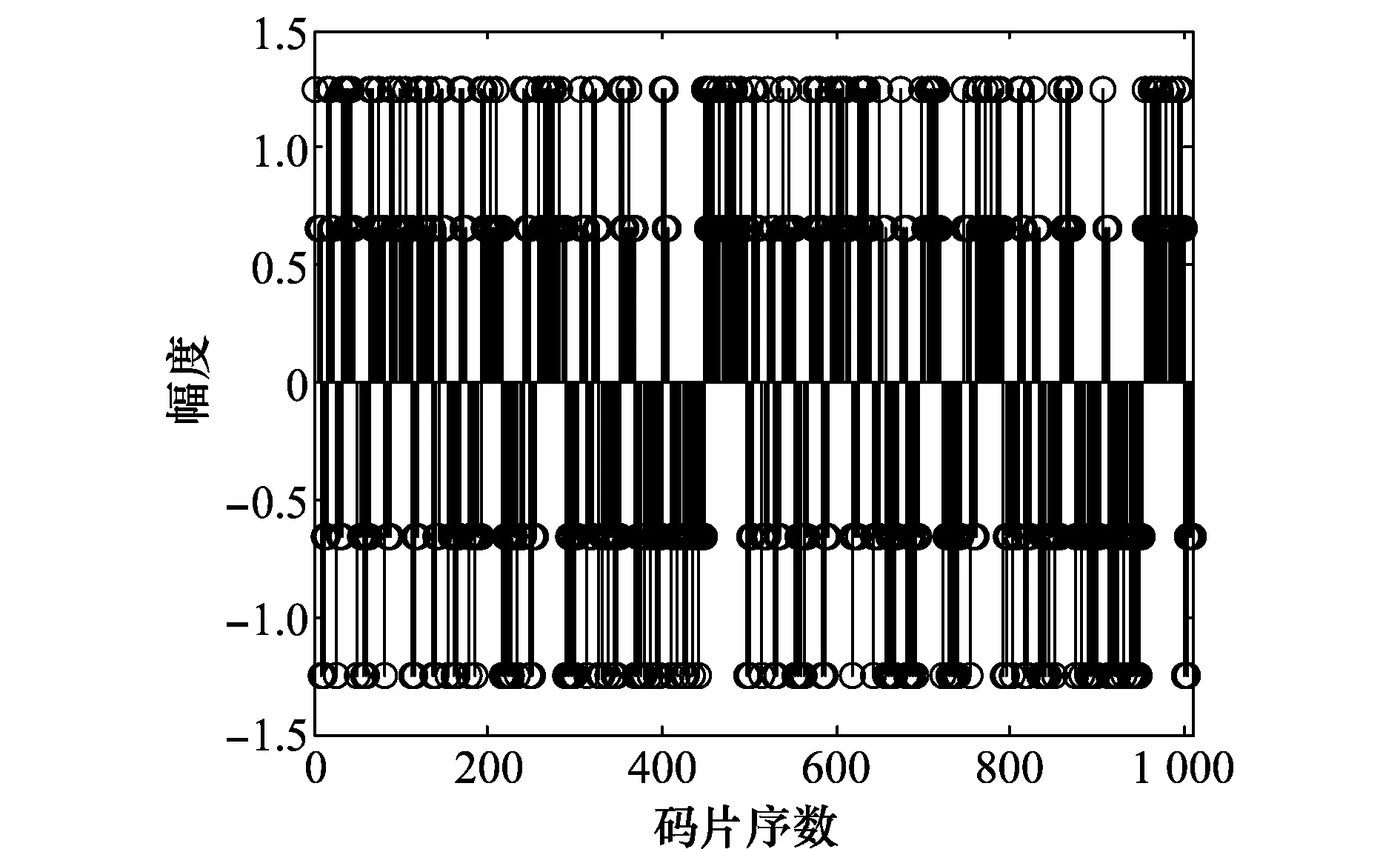
图7 CBOC信号原组合码序列Fig.7 Original combination code sequence of CBOC signal

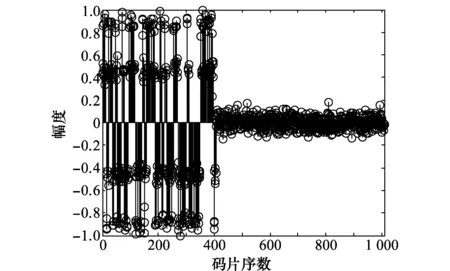
图对应的左奇异向量1Fig.8 Left singular vector 1 corresponding to

图对应的左奇异向量2Fig.9 Left singular vector 2 corresponding to

图对应的左奇异向量3Fig.10 Left singular vector 3 corresponding to

图6为按照升降顺序排列的矩阵R1对应的左奇异值谱,可以明显看出存在3个较大的左奇异值;图7为CBOC信号待估计的组合码序列;图8～图10分别是左奇异值谱对应的依次按降序排列的左奇异向量。由于文中将两周期的信号同时进行处理,图9为估计出的一个完整周期的组合码序列,图8结合图10为一个完整周期的组合码序列。实验1中选择的CBOC信号组合码周期为63×8=504,从估计出的组合码序列可以明显看出，序列呈现出两层分布状态,序列分布状态说明CBOC调制方式的引入使信号具有了高频信息,一定程度上增强了CBOC信号的码跟踪性能和抗干扰能力。

6.2 实验2

在验证了CBOC信号组合码序列盲估计具有可行性后,实验2为引入NN算法后的性能分析实验。在保持实验1中CBOC信号相关参数保持不变的情况下,依旧选取伪码长度L=63,副载波长度为8的CBOC进行此实验。上采样率Sa=1 bit/chip,进行100次蒙特卡罗仿真。

图11 学习收敛曲线Fig.11 Curve of learning convergence

图12 数据组数性能曲线Fig.12 Performance curve of data sets

图11、图12为采用NN算法进行100轮模拟实验后所得性能曲线,图11中表示在10个不同SNR下BER收敛至1%时的学习收敛曲线,图12为不同SNR下算法收敛所需的平均数据组数变化图。可看出算法在-18～0 dB所需数据组数较少,在-20～-18 dB所需数据数较多,因此图10中代表-20 dB学习收敛曲线距离其他几条收敛曲线较远,但实验结果表明NN的算法依旧能实现低SNR下CBOC信号的组合码序列盲估计。

6.3 实验3

分析NN算法在不同伪码以及不同副载波长度下,算法对CBOC组合码序列盲估计性能的影响。为清晰直观地观察算法性能,此处选取SNR∈[-15.56 dB,0 dB]的情况下进行性能分析。

由图13和图15可知,当CBOC信号组合码序列中伪码长度相同时,副载波长度越长,算法中BER降至允许的BER时所需的数据组数越少。由图14和图16可知,当CBOC信号组合码序列中副载波长度相同时,伪码序列长度越长时,算法中完全收敛时所需的数据组数越少。通过图13与图14可知,随着SNR的不断降低,NN算法完全收敛所需的平均数据组数也在逐渐增加。

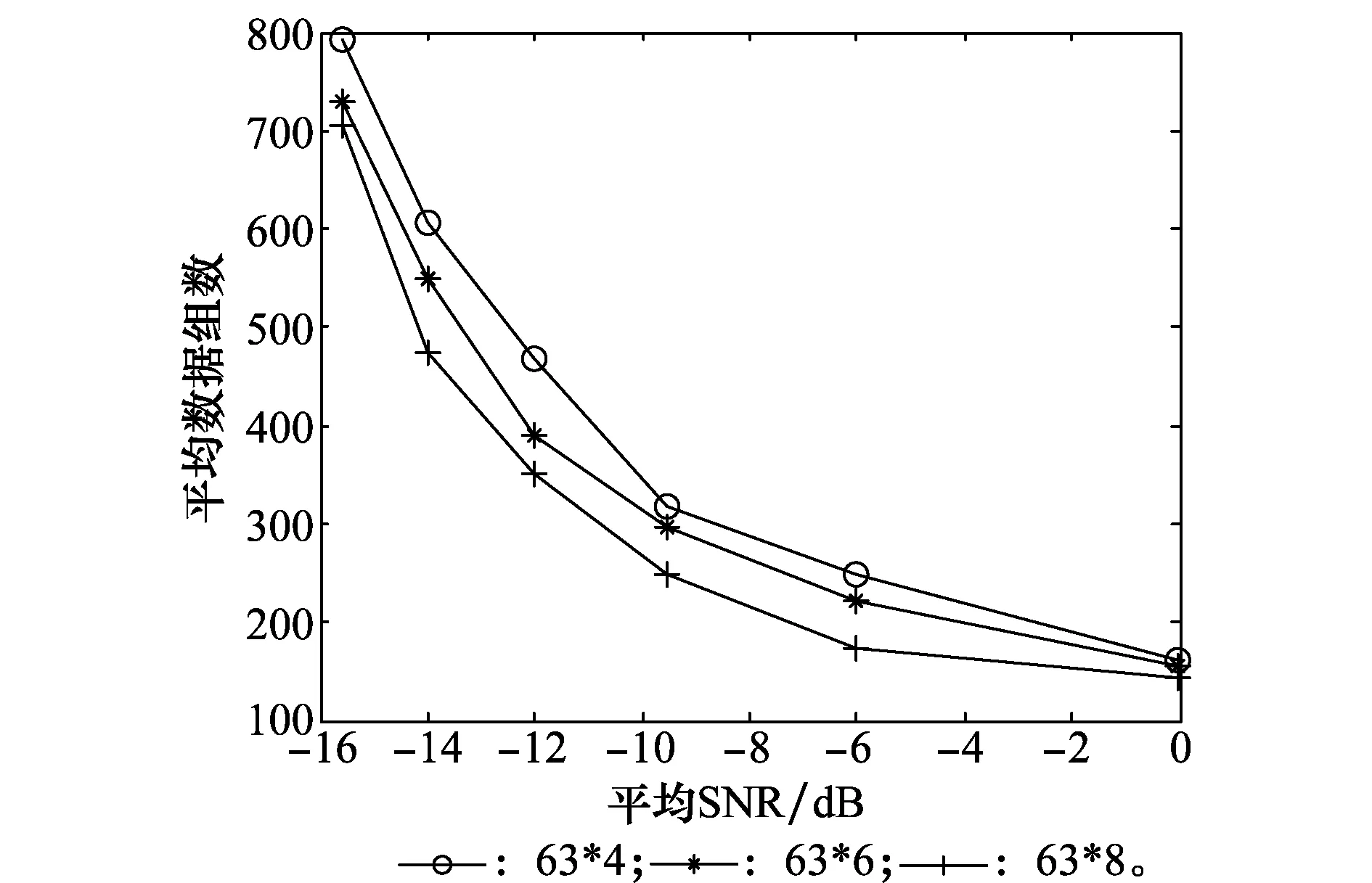
图13 不同副载波长度下的数据组数性能曲线Fig.13 Performance curves of data sets under different subcarrier lengths

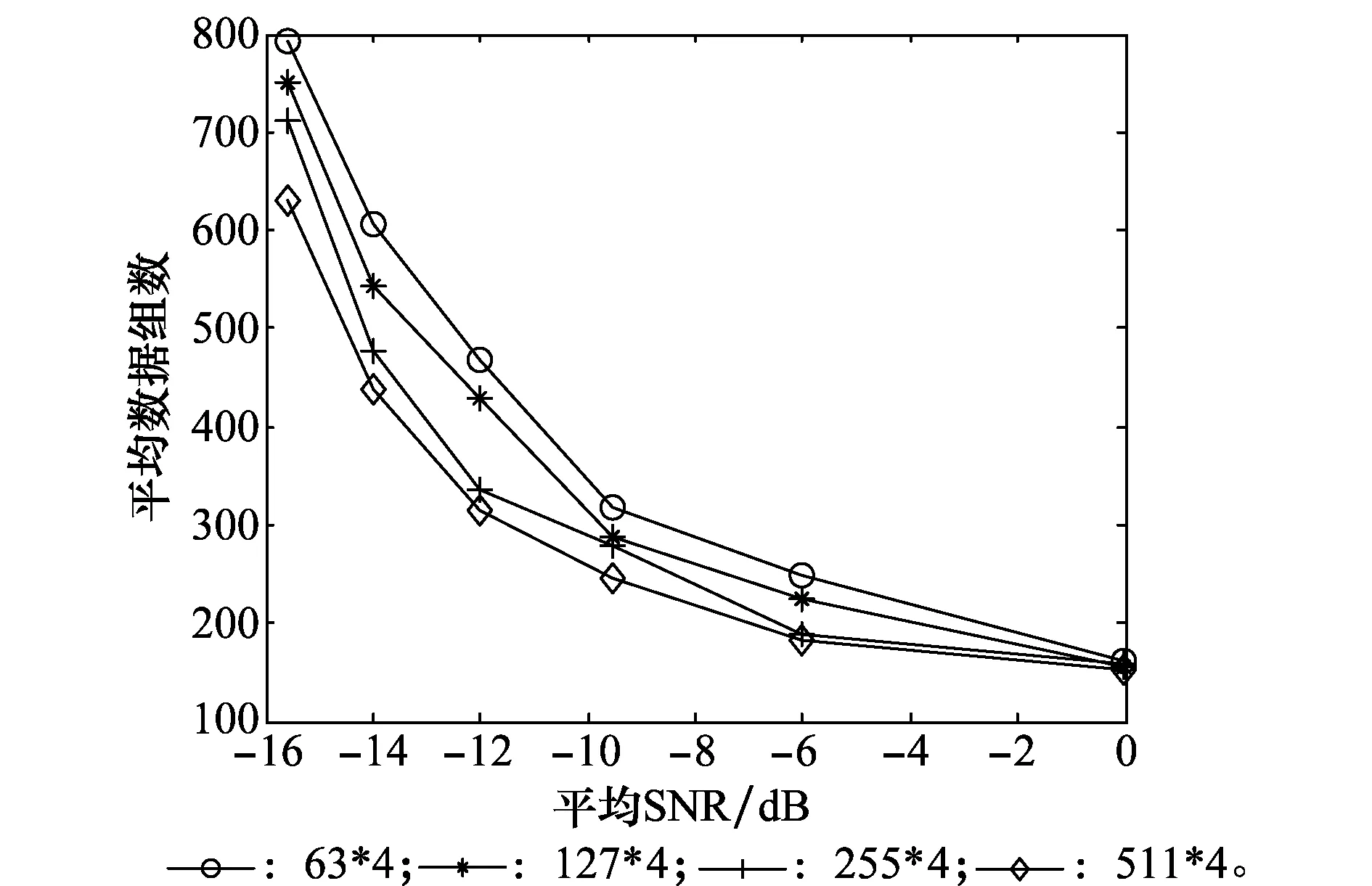
图14 不同伪码长度下的数据组数性能曲线Fig.14 Performance curves of data sets under different pseudo code lengths

图15 不同副载波长度下的学习收敛曲线Fig.15 Learning convergence curves under different subcarrier lengths

6.4 实验4

研究不同上采样率对NN算法性能的影响。此处选取SNR为-14 dB,伪码长度为63,副载波长度为4的CBOC信号进行仿真实验。

图16 不同伪码长度下的学习收敛曲线Fig.16 Learning convergence curves under different pseudo code lengths

图17 不同上采样率下的学习收敛曲线Fig.17 Learning convergence curves under different sampling rates

图17表示在算法中其他参数均相同的情况下,上采样率取值越大,算法性能越好,即BER降至允许的最低BER时需要的数据组数明显更少。从图17中可看出，当上采样率取值为8 bit/chip时,算法性能大幅提升,与上采样率取值为1 bit/chip时所需数据组数的对比非常明显。

6.5 实验5

CBOC信号中组合码由副载波与伪码组成,将其与直扩信号进行仿真结果的对比,分析副载波对组合码估计过程中的影响。

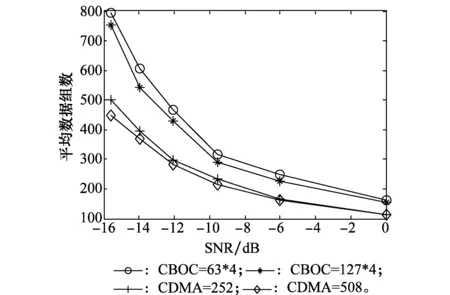
图18 均值性能曲线Fig.18 Performance curve of mean

图18中选取伪码长度等于组合码长度的直扩信号进行仿真分析,由图18可明显看出组合码中副载波的存在对信号序列估计产生的影响较大,当直扩信号伪码长度等于CBOC组合码长度时,直扩信号收敛所需数据组数明显少于CBOC信号。

6.6 实验6

为进一步验证本文采用的NN算法对CBOC信号组合码序列估计的性能,SNR选取[-15.56 dB,-4 dB],分别对每个SNR对应的组合码序列估计进行100次蒙特卡罗仿真,并和文献[13]中的自相关搜索算法进行对比,仿真结果如图19～图20所示。

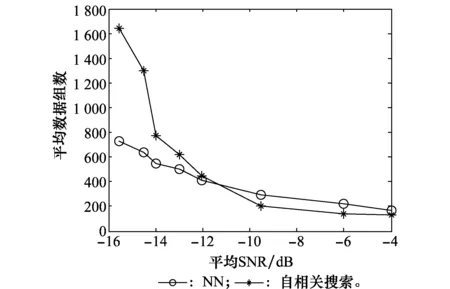
图19 测量数据组数均值比较Fig.19 Comparison of mean values of measured data groups

图20 测量数据组数的均方根误差比较Fig.20 Comparison of square root error of the number of measured data groups

图19反映的是NN和自相关搜索算法的性能估计曲线,以平均SNR为横坐标,分别表示了在不同SNR下两种算法正确地盲估计出信号的组合码序列所需的平均数据组数。相同条件下,本文所采用的NN算法正确估计序列所需数据组数在低SNR的情况下明显少于自相关搜索算法;图20所示的均方根误差大小反映了收敛时间的稳定性高低,本文算法的均方根误差在低SNR的条件下远低于自相关搜索算法。综上所述,本文采用的NN算法在不同SNR下完成收敛所需的数据组数以及算法的稳定性均优于自相关搜索算法。

7 结 论

针对CBOC信号组合码序列盲估计问题,本文首先利用以两倍信息符号周期长度分段的SVD算法来验证CBOC调制信号的组合码序列盲估计的可行性;其次引入NN的方法来解决传统SVD算法对内存要求过高、复杂度较高的缺点,且为改善算法收敛速度,引入变步长收敛模型。理论分析与仿真实验表明,SVD算法与NN算法对实现CBOC信号组合码序列的盲估计有效,且NN算法可实现-20～0 dB下CBOC信号组合码序列的盲估计。相比其他算法,NN算法具有复杂度低,算法稳定性高、收敛速度快等优点。另外,NN能够自适应地处理输入数据且不需要存储权值更新的中间变量,因此可以工作在长输入环境和非平稳环境中。本文研究为电子对抗中信息序列的盲估计奠定基础,为最终实现信号的盲解扩提供有力条件。