惯导系统陀螺漂移的ESO估计算法
2018-12-10夏卫星杨晓东
夏卫星,杨晓东
(海军潜艇学院航海观通系,山东 青岛 266199)
0 引 言
惯导系统能够完全自主地提供舰艇经纬度位置、航行速度、航行姿态等信息,其不仅能够保障舰艇的航行安全,而且为舰(艇)载武器系统提供基准信息源。然而,由于陀螺漂移等其他惯性器件误差的存在,使得惯导系统呈随时间不断积累的误差特性,导航精度无法满足实际要求。因此,必须对其进行陀螺漂移估计(又称综合校正),通常采用两点校、三点校和点点校等[1]。
“两点校”对外部信息的要求较高,需要位置及方位信息;“三点校”需要以一定的时间间隔连续观测3次位置信息,从而估计出陀螺漂移进行补偿并对位置误差进行修正[2-4]。文献[5]指出,惯导系统进行陀螺漂移估计时,需处于水平阻尼状态,且保持匀速直航向航行,否则引入水平姿态角误差,估计精度无法保证,甚至会发散。文献[6]以“两点校”为例,从理论上探讨分析了现行陀螺漂移估计算法的不足。文献[2]提出了针对捷联惯导系统的陀螺漂移估计补偿技术,该算法以“三点校”为基础,利用较长时间间隔获得的外部位置信息,建立其与陀螺漂移和方位误差的关系式,再利用最小二乘法算出陀螺漂移并进行方位误差补偿。
由文献分析可见,“两点校”算法耗时较长,在系统第一次重调后,陀螺漂移需间隔4~6 h才能得到精确补偿,然而在相当长的校正时间间隔内,惯导系统的导航精度无法保证,“三点校”则需要的时间更长。尤其对水下潜艇而言,其隐蔽性必然受到影响。由此可见,面对现代复杂的海战场,传统综合校正的估计精度和适用性无法保证。
为确保陀螺漂移估计精度,满足舰(潜)艇平台的实际应用需求,从惯导系统姿态控制方程着手,基于扩张状态观测器(extended state observer,ESO)提出了一种全新的陀螺漂移估计方案,能够在短时间内快速、无超调、高精度地估计陀螺漂移。
1 ESO的设计原理
ESO能够实现跟踪被控对象的输出,对各阶状态变量和扰动进行实时估计[7]。ESO不依赖于具体的系统模型。因此,ESO是通用且实用的状态观测器。ESO是一个动态过程,仅仅利用被控对象的输入和输出信息,不需具体的模型描述[7-13]。
ESO与普通的状态观测器不同,其可有效观测扩张的状态变量,实时估计系统中未建模部分,将非线性的控制对象变为普通的积分串联型控制对象[14-17]。其基本结构如图1所示。
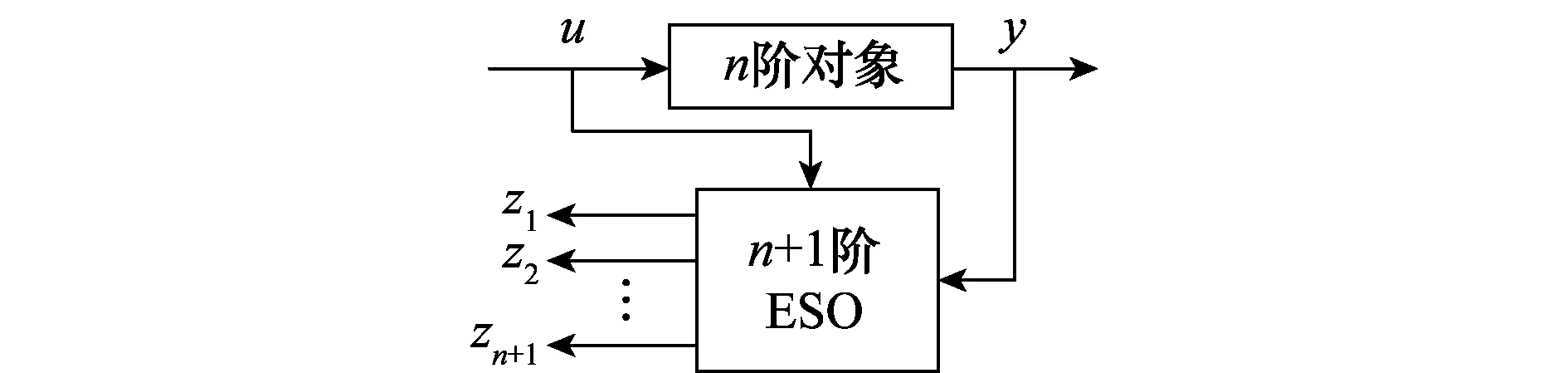
图1 n+1阶ESO结构Fig.1 n+1 order structure of ESO
基于上述原理,考虑非线性系统
(1)
其非线性状态观测器为
(2)
式中,e1为输出误差;z1为状态变量;β01、β02为适当的参数;b为控制变量u的系数。

(3)
则该扩张系统的状态观测器[18-20]为
(4)
由上述文献分析可见,ESO是一动态过程,它只需利用系统的输入—输出信息,无需假定f(x1(t),x2(t),t,ω(t))是否连续,是否已知,只要f(x1(t),x2(t),t,ω(t))有界,且参数b已知,选择适当参数β01,β02,β03,即可很好地实时估计式(3)的状态变量x1(t),x2(t),以及被扩张的状态的实时作用量x3(t)=f(x1(t),x2(t))。
2 水平姿态角的ESO估计
惯导系统作为一非线性系统[1,21-24],若对其水平姿态角实现快速、无超调的精确跟踪与估计,必须选择合适的非线性状态跟踪估计器。ESO作为典型的非线性估计器,其不要求事先知道水平姿态角的均值与方差,即可实现精确估计与跟踪。
对垂向比力分量不作简化处理,考虑惯导系统速度误差[21,25]:
(5)
式中,Ω为地球自转角速度;vx、vy为东、北向速度;δvx、δvy为东、北向速度误差;φ、λ为纬度和经度;δφ、δλ为位置误差;α、β为惯导水平姿态角;ΔAx、ΔAy为东向、北向加速度计零偏;R为地球半径。
令速度误差为系统量测量,则与式(5)对应的系统量测方程为

(6)
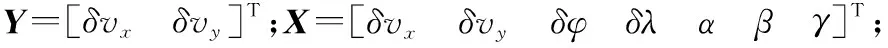
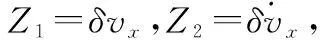
(7)
对式(7)构造ESO
(8)
式中,h、a、δ、B1、B2为ESO参数;fal函数及ESO各参数定义详见文献[7]。
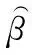
(9)
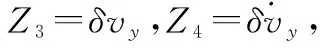
(10)
式中,B3、B4为ESO参数,其余各参数定义同上。
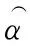
(11)
可知,只需获取精确的外界信号即可实现水平姿态角的准确估计。
3 陀螺漂移的ESO估计
由于众多影响因素的存在,导致惯导系统无法准确无误的模拟地理坐标系,必然存在姿态偏差,其中,陀螺漂移为主要因素。
考虑惯导系统姿态控制与陀螺漂移的内在联系,得
(12)
式中,γ为方位姿态角,其余参数定义同上。
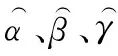
考虑

(13)

(14)
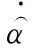
(15)
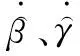
由此,基于ESO,即可运用式(12)对陀螺漂移进行实时估计,即
(16)
式(12)估计的稳态误差为
(17)
4 算法估计流程
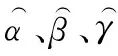
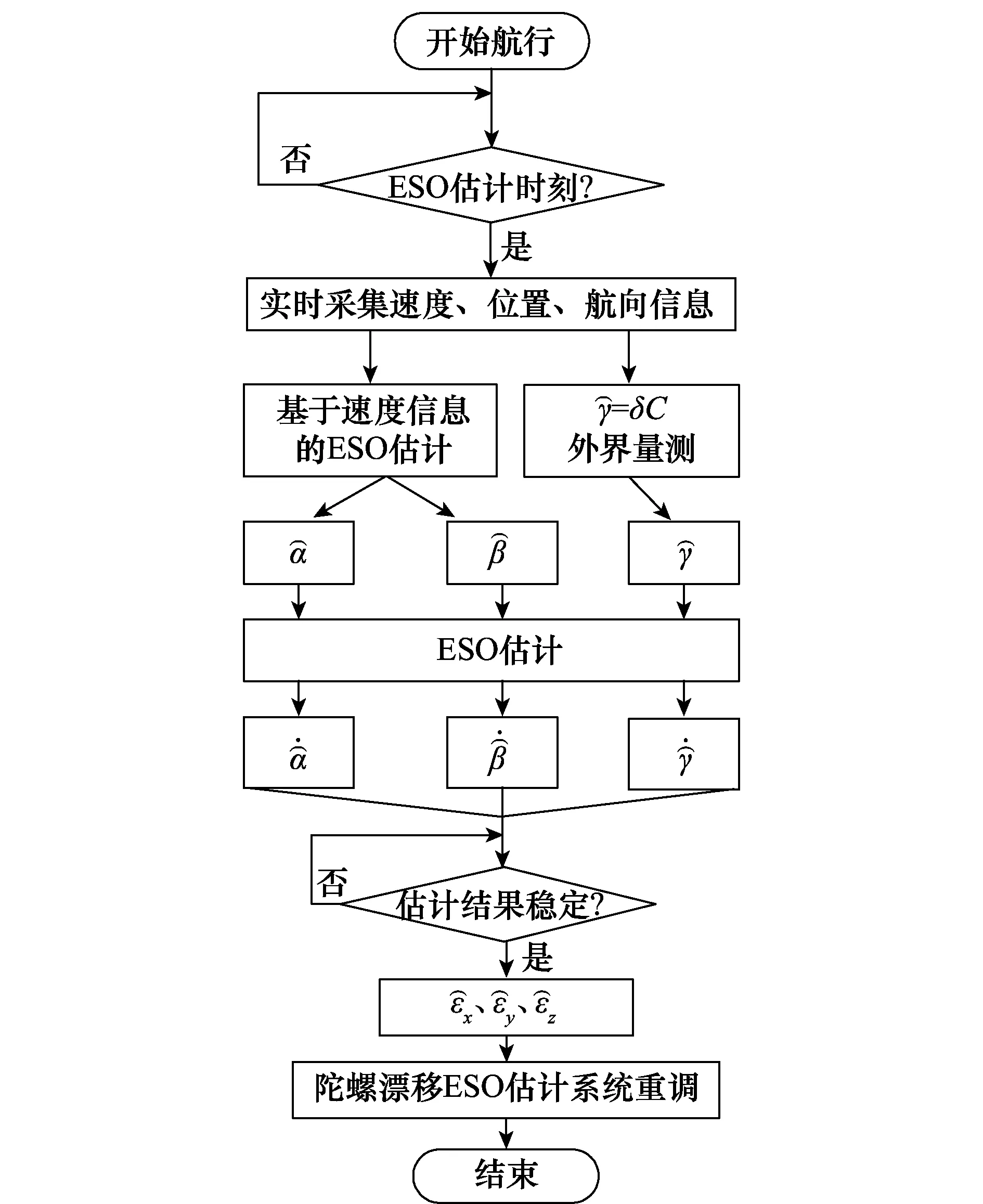
图2 陀螺漂移ESO估计算法流程Fig.2 ESO estimation algorithm flow of gyro drift
5 算法仿真与实验
仿真条件设定:
(1) 舰艇航行参数设定
航行速度v=10 kn;
航向H=60°;
初始位置φ=36°N、λ=122.2°E。
(2) 惯导系统参数设定
姿态初始误差α=3′,β=3′,γ=5′;
加速度计零位偏置ΔAx=ΔAy=10-5g;
陀螺常值漂移:εx=0.002 (°)/h,εy=0.002 (°)/h,εz=0.002 (°)/h。
(3) 外界量测信息精度设定
速度误差为σvrx=σvry=0.02 m/s;
航向误差为10″。
(4) ESO参数选择
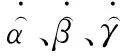
(5) 数据采样间隔t=0.1 s。
估计方案:惯导系统工作于水平阻尼状态,t=10h00m~10h04m,惯导系统开始陀螺漂移ESO估计,接收位置、速度以及航向信息。采用ESO估计惯导系统水平姿态角,同时基于估计出的水平姿态角及航向量测信息估计水平姿态角的微分信号,由式(16)快速求解惯导系统陀螺漂移,待估计结果稳定后(t<1 min),t=10h05m补偿系统陀螺漂移并对系统位置、航向重调,估计补偿结束,t=10h05m~36h00m观察各状态误差发散情况。
由图3可知,ESO可在较短时间内,以最快的速度估计出平台水平失调角,具有较好的响应特性,估计结果稳态精度高,短时间内即可达到稳态。
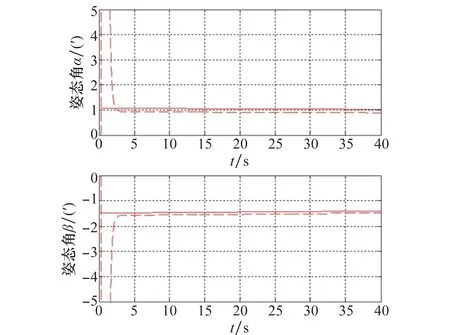
图3 水平姿态角的ESO估计Fig.3 ESO estimation of horizontal attitude angle
图4~图6为惯导系统陀螺漂移的ESO估计曲线,图中粗实线为设定值,细实线为ESO估计值。基于水平姿态角的估计值,短时间内(t<1min)可实现陀螺漂移的准确估计。相对传统综合校正,在保证陀螺漂移估计精度的前提下,时间大幅缩短。对军用舰艇,尤其对潜艇而言,能够有效降低暴露概率,提高潜艇隐蔽性。
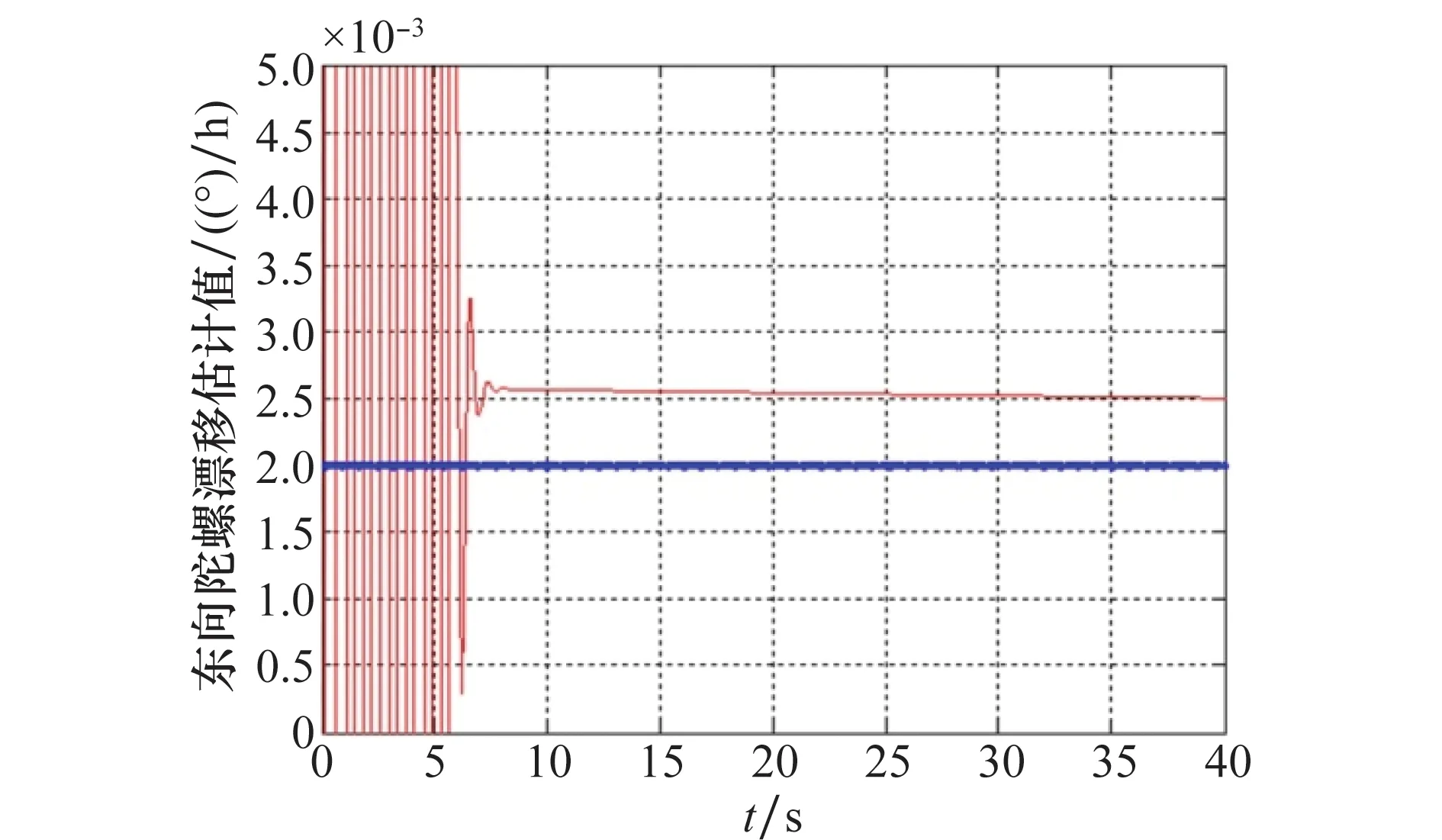
图4 东向陀螺漂移的ESO估计Fig.4 ESO estimation of east gyro drift
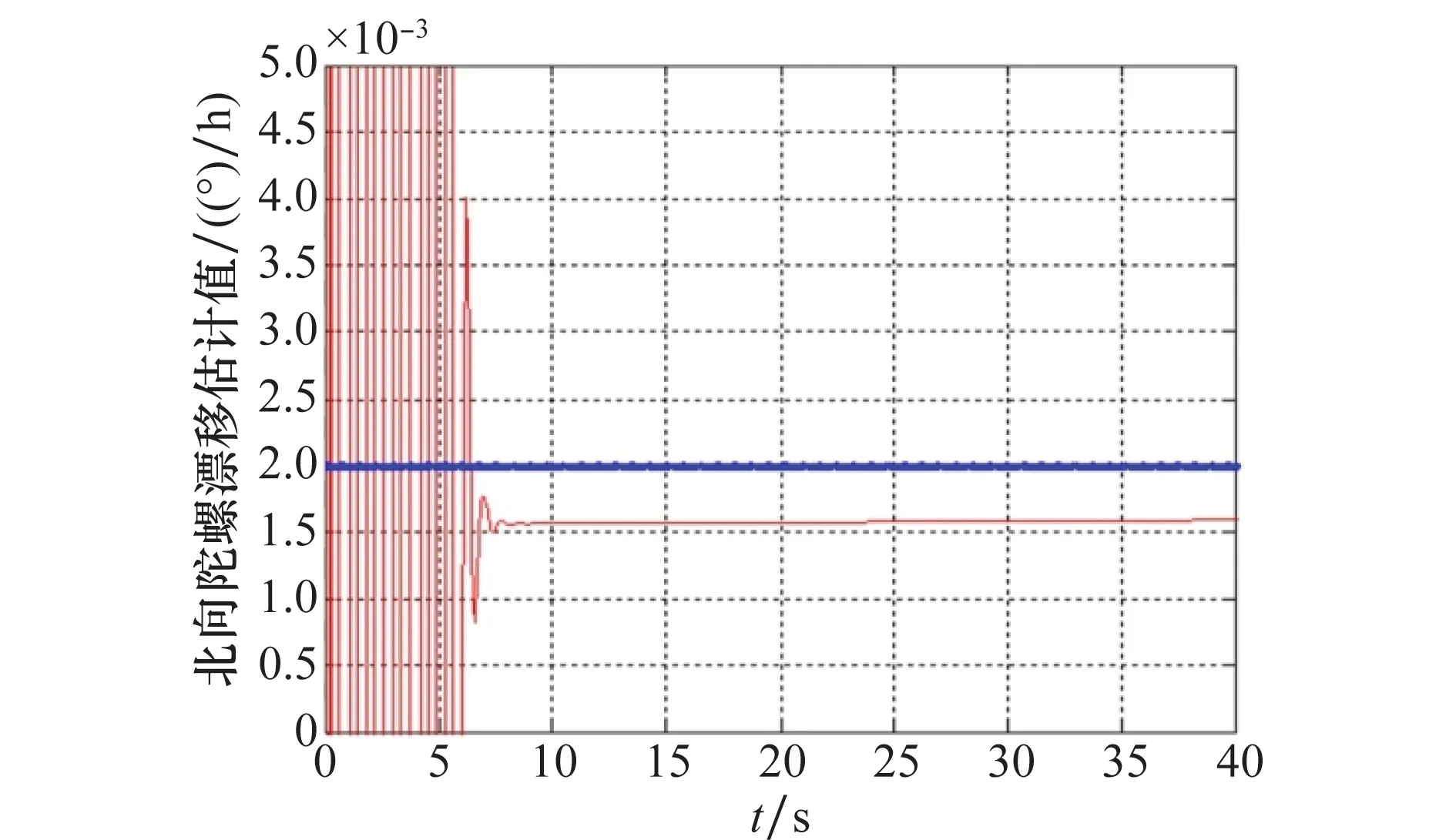
图5 北向陀螺漂移的ESO估计Fig.5 ESO estimation of north gyro drift
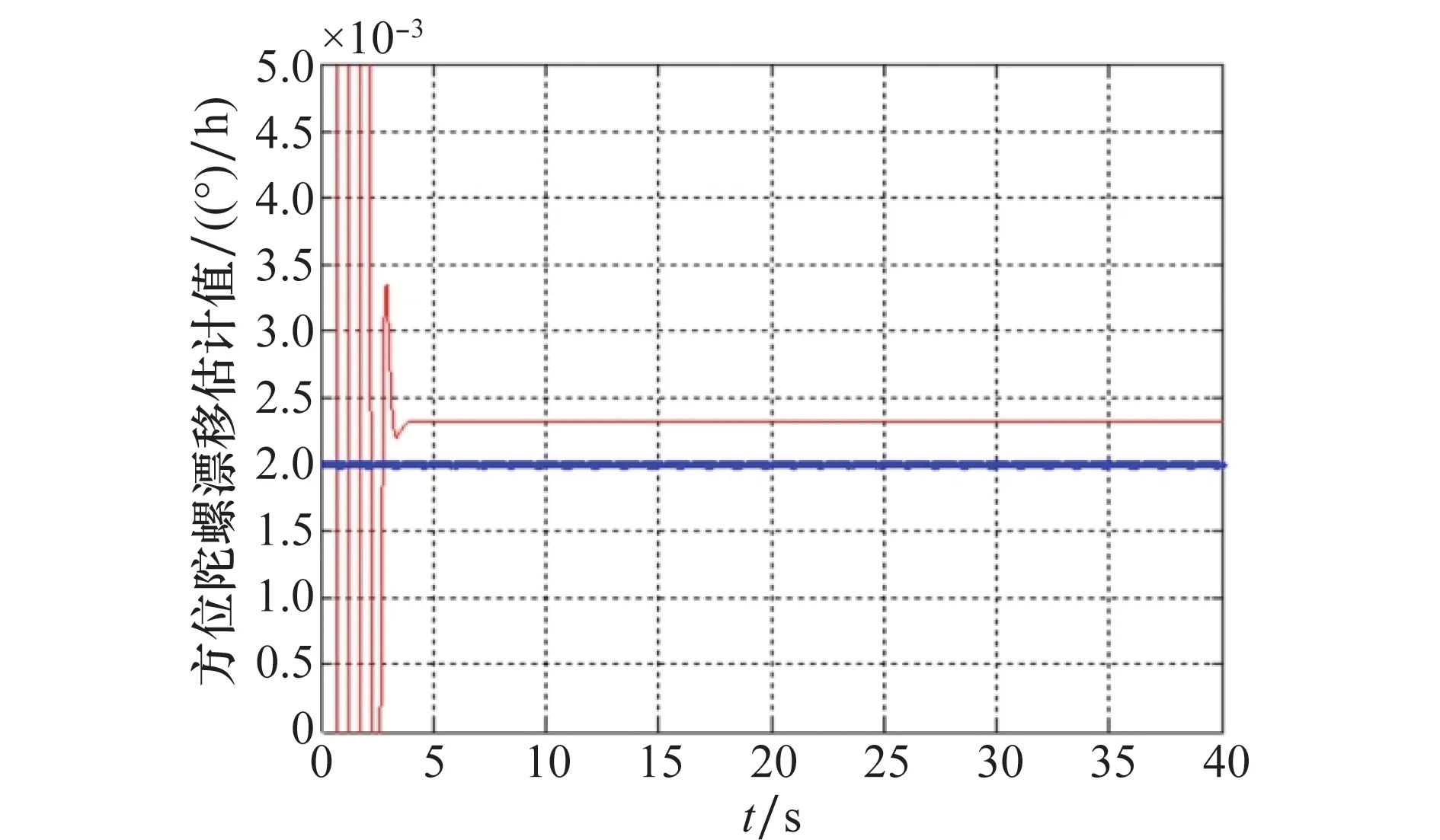
图6 方位陀螺漂移的ESO估计Fig.6 ESO estimation of position gyro drift
基于设定的仿真条件,采用式(17)对陀螺漂移ESO估计的稳态误差进行量化分析,得
由定量分析结果可知,ESO估计算法解得的陀螺漂移估计稳态误差量级为10-4(°)/h,该稳态误差对陀螺漂移的估计影响较小。由公式(17)分析可见,该稳态误差量级取决于加速度计零位偏置ΔAx、ΔAy的精度限制。
图7为实施陀螺漂移ESO估计方案后,惯导系统各状态误差的发散,图7中,实线为ESO估计补偿结果,虚线为未补偿。由图7可见,由于对陀螺漂移进行了高精度的估计和补偿,系统导航误差明显降低,表明设计的陀螺漂移ESO估计方案有效。
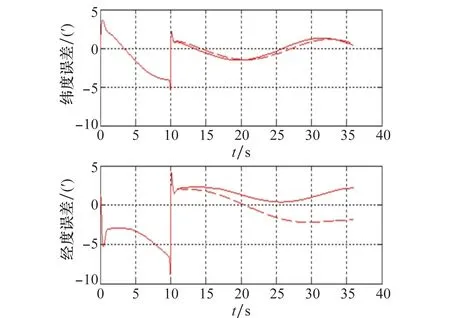
图7 估计补偿后的惯导系统误差Fig.7 Inertial navigation system system error after estimated compensation
6 结 论
传统的惯导系统陀螺漂移估计方法(两点校)耗时长(约4~6 h),三点校则需更长时间,且校正精度受航行状态影响,对于军用舰艇,尤其是潜艇而言,其适用性不强。基于此,论文提出了陀螺漂移的ESO估计方法,从惯导系统控制方程着手,针对其内在联系,基于ESO实现了陀螺漂移快速估计。该算法不受舰艇航行状态约束,所需时间短、估计精度高,对于军用舰艇惯导系统具有较强的实际应用价值。
