切比雪夫距离下系统置换码的编译码算法
2018-12-10慕建君焦晓鹏
韩 辉,慕建君,焦晓鹏
(西安电子科技大学 计算机学院,陕西 西安 710071)
目前,多级存储单元(Multi-Level Cell,MLC)技术能够提高NAND闪存的数据存储密度(容量). 然而,随着NAND闪存芯片封装尺寸的缩小,大容量、高可靠闪速存储器的研究及应用面临着闪存单元编程和单元擦除之间的非对称性问题. 2009年,文献[1]提出的等级调制方案给出了解决这一问题的一种新框架. 该方案中,数据的存储是以单元间电荷值相对等级的形式表示,而不是以电荷绝对等级的形式表示.
闪存面临的第2个问题是所存储数据的可靠性问题,特别是多级存储单元型闪存中出现的单元间干扰(Cell-to-Cell Interference)现象使得数据损坏的问题更为突出[2]. 基于等级调制方案的纠错置换码可以提高闪速存储设备数据存储的可靠性[3-6]. 基于等级调制方案的纠错置换码的大多数研究主要选择切比雪夫距离度量和Kendallτ-距离度量. 文献[7]中关于等级调制纠错码的研究表明,闪存单元发生的小电荷受限错误(Charge-Constrained Error)对应一个小的Kendallτ-距离,而文献[8]的研究表明,闪存单元发生的小强度有限错误(Limited-Magnitude Error)对应一个小的切比雪夫距离度量.
针对Kendallτ-距离度量,文献[7]利用测度嵌入技术提出了Kendallτ-距离度量下可以纠正单个相邻对换错误的置换码的构造方法. 而针对切比雪夫距离度量,文献[8]设计了可以纠正闪存单元幅度为t的强度有限错误的子群置换码.2015年,文献[9]构造了Kendallτ-距离度量和切比雪夫距离距离度量下基于等级调制方案的两类系统置换码,同时给出了所构造Kendallτ-距离度量下系统置换码的编译码思路.
尽管文献[9]提出了切比雪夫距离度量下基于等级调制方案的系统置换码的构造方法,但是没有给出该类系统置换码的编码和译码方法. 基于文献[8]所设计的切比雪夫距离度量下的(n,M,d)子群置换码的编译码思路,通过利用对称群上的ranking与unranking映射以及(n,M,d)置换码的交织技术,提出了 [k+n,k,d]系统置换码的一种编码算法. 同时,借助利用对称群上的ranking与unranking映射以及切比雪夫距离度量下(n,M,d)置换码的投影技术,提出了该 [k+n,k,d]系统置换码的一种译码算法.
1 置换理论
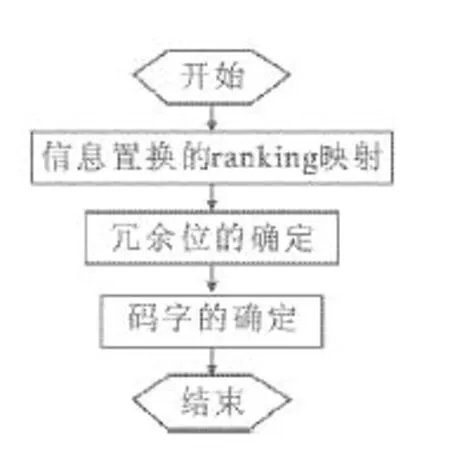
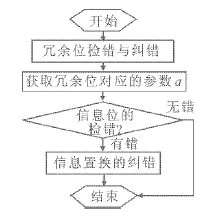
设[m,n]表示由n-m+1个整数组成的集合{m,m+1, …,n},其中m∈N,n∈N(m 下面给出置换交织[10]、置换逆序[7]、切比雪夫距离度量[8,11]、系统置换码[9]等与置换相关的几个定义. 定义2 对于给定集合A={a1,a2, …,an}上对称群SA的置换f= (f(1),f(2), …,f(n))∈SA,若i 定义4 对于给定集合A上的置换f∈SA和子集B⊆A,通过保留f中属于B的元素而去掉其他所有元素后得到的置换称为f在集B上的投影,记为f|B.例如,对于置换f= (6, 4,3, 1,5, 2)∈S6和子集B= {2, 4, 6}⊆A= {1,2,3,4,5,6},f在B上投影f|B= (6,4,2). 定义5 对于给定的对称群S[n+1,n+k],若一个(k+n,k!,d)置换码C满足 {g|[n+1,n+k]|g∈C}=S[n+1,n+k],则称置换码C为一个 [k+n,k,d]系统置换码.[k+n,k,d]系统置换码C的任意一个码字的第1到k位表示码字的信息位,而其第k+1 位到第n+k位表示码字的冗余位. 对于集合A上的对称群SA,为了建立字典序排序中置换f∈SA与其对应位置的关系,Lehmer给出了对称群上的ranking及unranking映射的具体方法[11]. 借助文献[12]所构造的(n,M,d)置换码Cr,文献[9]提出了切比雪夫距离度量下 [k+n,k,d]系统置换码Cs的一种构造方法,即: 构造1 对于给定的正整数d(1≤d≤n),令Cr= {f∈Sn|f(i)≡i(modd),i∈ [1,n]},则Cr是一个(n,M,d)置换码[12],且Cr的码字个数 (1) 令k是满足M≥k!的最大正整数,S[n+1, n+k]表示[n+1,n+k]上所有置换的集合.假定Cr= {f1,f2, …,fM}和S[n+1, n+k]= {g1,g2, …,gk!},则可构造得置换码Cs= {gi‖fi|i∈ [k!]},其中‖表示向量的级联. 由文献[9]可知,构造1所得的置换码Cs={gi‖fi|i∈[k!]}是切比雪夫距离度量下的 [k+n,k,d]系统置换码. 系统置换码的编码: 文献[9]构造的切比雪夫距离度量下[k+n,k,d]系统置换码Cs编码的关键是建立码字中信息位与冗余位之间确定的对应关系. 笔者利用对称群上的ranking及unranking映射和(n,M,d)置换码Cr的一种交织编码方法来建立信息位与冗余位之间的对应关系. 图1 [k+n, k, d]系统置换码的编码算法流程图 假设信息置换m=(m(1),m(2), …,m(k))∈S[n+1, n+k],而通过切比雪夫距离度量下 [k+n,k,d]系统置换码Cs编码得到的码字为c= (c(1),c(2),…,c(k),c(k+1),…,c(k+n)).对于集合[n],令Ai= {j∈ [n]|j≡i(modd)},其中i∈ [d].下面给出切比雪夫距离度量下可以纠正“强度有限错误”的 [k+n,k,d]系统置换码的编码算法(为了描述方便,假定d|n,且令t=n/d,该系统置换码的编码算法流程图如图1所示): (1) 信息置换的ranking映射: 对于信息置换m∈S[n+1, n+k],利用对称群S[n+1, n+k]上的映射ranking:S[n+1,n+k]→ [0,k!-1] 得 ranking(m)=a. (3) 码字的确定: 由信息置换m编码得到的 [k+n,k,d]系统置换码Cs的码字c=m‖α. 例3 考虑构造1所给出的[3+6,3, 3]系统置换码Cs,其中Cs的冗余位是利用构造1的方法所得到的(6, 8, 3)置换码Cr. 对于 [3+ 6, 3, 3]系统置换码Cs,令t= 6/3= 2,下面给出一个码字信息位m= (7, 9, 8)∈S[7, 9]的 [3+ 6, 3, 3]系统置换码Cs的编码过程: (1) 信息置换m=(7, 9, 8)的ranking映射: 对于[3+6, 3, 3]系统置换码Cs的信息置换m= (7, 9, 8)∈S[7, 9],利用对称群S[7, 9]上的映射ranking:S[7, 9]→ [0,3!-1] 计算得 ranking(m)= 0· 0!+ 1· 1!+ 0· 2!=1=a. (2) 冗余位(c(4),c(5),c(6),c(7),c(8),c(9))的确定: 将a=1表示成2!进制形式 1= 1· (2!)0+ 0· (2!)1+ 0· (2!)2得(a1,a2,a3)= (1, 0, 0) ; 然后,利用Ai= (j∈ [6]|j≡i(mod 3)) (i∈ [3])可得A1= {1,4}、A2= {2,5}与A3= {3,6}; 利用对称群SAi上的映射unranking: [0, |Ai|!-1]→SAi(i∈ [3]), 可得到(a1,a2,a3)= (1, 0, 0)的分量a1=1 所对应集合A1上的置换 unranking(1)= (4, 1)、a2=0 所对应集合A2上的置换 unranking(0)= (2, 5)和a3=0 所对应集合A3上的置换 unranking(0)= (3, 6); 从而利用向量交织方法得到信息置换m= (7, 9, 8)∈S[7, 9]所对应码字c的冗余位(c(4),c(5),c(6),c(7),c(8),c(9))= (4,1)∘ (2,5)∘ (3,6)= (4,2,3,1,5,6). (3) 码字c的确定: 由信息置换m=(7, 9, 8)∈S[7, 9]编码得到的[3+6, 3, 3]系统置换码的码字c= (c(1),c(2),c(3),c(4),c(5),c(6),c(7),c(8),c(9))= (7, 9, 8)‖ (4, 2, 3, 1, 5, 6)= (7, 9, 8, 4, 2, 3, 1, 5, 6). 针对上节所给出的[k+n,k,d]系统置换码Cs的编码方法,利用对称群上的ranking和unranking映射及文献[12]给出的切比雪夫距离度量下(n,M,d)置换码的译码思路,下面提出了切比雪夫距离度量下可纠幅度至多为l的强度有限错误 [k+n,k,d]系统置换码Cs的一种译码算法 (d≥ 2l+1,l≥0). 图2 [k+n, k, d]系统置换码的译码算法流程图 (4) 信息置换的纠错: 对于步骤(2)中所得到的冗余位对应的参数a,利用对称群S[n+1, n+k]上的映射unranking: [0,k!-1]→S[n+1,n+k]得到正确的信息位m= unranking(a)= (c(1),c(2), …,c(k))∈S[n+1, n+k]. 针对文献[9]所构造的切比雪夫距离度量下可以纠正“强度有限错误”的 [k+n,k,d]系统置换码缺乏编译码方法的问题,利用对称群上的ranking与 unranking映射以及切比雪夫距离度量下(n,M,d)置换码的交织技术,笔者提出了该系统置换码的一种编码方法及其相应的译码方法. 通过计算实例,说明了文中所提出的切比雪夫距离度量下 [k+n,k,d]系统置换码编码方法及其相应译码方法的正确性.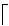
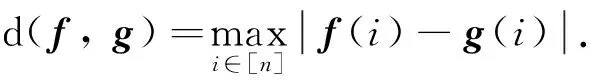
2 Ranking置换
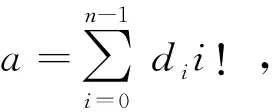
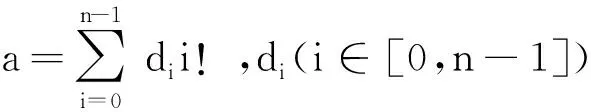
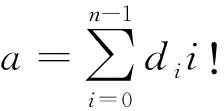


3 系统置换码的编码算法

4 系统置换码的译码算法


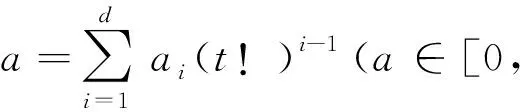


5 结 束 语
