一种稀布阵列天线的近场波束综合算法
2018-12-07宋嘉奇陶海红
宋嘉奇,陶海红
(西安电子科技大学 雷达信号处理国家重点实验室,陕西 西安 710071)
稀布阵列天线孔径更大,拥有主瓣窄、分辨率高、成本低等优点,应用范围非常广泛[1],因此稀布阵列天线的综合问题一直都是研究的热点.

图1 近场区域波束聚焦失配图
阵列响应是阵元位置的复指数函数,针对天线位置的综合问题是一个非线性优化问题,很多学者对远场情况下的稀布阵列天线综合问题开展了研究,提出了模拟退火法[2-3]、遗传算法[4-5]、粒子群算法[6]和黑洞算法[7]等优化求解的方法,对阵列的空间响应性能(如主瓣宽度,峰值旁瓣电平(Peak Side-Lobe Level,PSLL)等)进行优化,取得了很好的实验效果.在网络化雷达背景下,大的天线孔径导致近场范围扩大会带来异常严重的近场问题,而很多感兴趣的目标都在近场范围内.从天线表面到 2D2/λ的空间范围被认为是近场区域[8],其中,D为天线有效孔径,λ为波长.若采用传统的远场阵列方向图会造成阵列天线主瓣和副瓣的畸变,影响波束形成的性能,如图1所示.可以看出,在近场区域波束方向图的主瓣位置有一定的弯曲,此时需要对感兴趣的目标区域进行主波束的聚焦修正.此外,近场聚焦波束形成还在声纳探测、麦克风阵列等场景中有着广泛应用.
针对近场电磁波传播时延参数表达式比较复杂的情况,文献[9]对近场散射效应提出了一种基于导向矢量不确定集的稳健自适应波束形成算法;文献[10]提出了采用菲涅尔近似作为时延参数的近似表达式的思路;文献[11]指出菲涅尔近似可作为近场情况下时延参数近似表达式的3个条件.可以看出,菲涅尔近似成立的距离和角度范围均比较有限;文献[12-13]对菲涅尔近似进行了一定的改进,增大了菲涅尔近似的可适用范围.但在适用范围之外,时延参数近似对波束形成性能的影响较大.笔者针对这一问题,提出了一种基于差分进化(Differential Evolution,DE)算法[14-15]的稀布阵列综合的方法,在全域内控制峰值旁瓣电平.
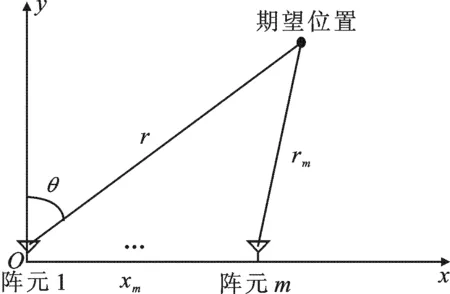
图2 稀布直线阵列示意图
1 信号模型与问题描述
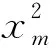
(1)
该稀布阵列的阵列流形为
(2)
波束响应可以用来考察稀布阵列天线的空间响应特性,可以表示为
(3)
其中,w0是加权向量,当不考虑稀布阵列各天线单元激励时,w0为期望位置(r0,θ0)所对应的阵列流形a0,即
(4)


2 基于差分进化算法的近场波束综合算法
DE算法是一种基于群体差异的启发式随机搜索算法,其应用简单,鲁棒性好且全局搜索能力强,是解决优化问题的一种有效工具[11-12].DE算法首先从一组随机产生的初始种群随机选择两个不同的个体向量相减生成差分向量,将差分向量赋予权值后与第3个随机选择的个体向量相加,产生变异向量.然后将变异向量与预先确定的父代个体向量按一定的规则交叉产生试验向量.若试验向量的适应度值优于父代个体向量的适应度值,则选用试验向量进入下一代;否则,则保留父代个体向量.通过不断的进化,保留优胜的个体,引导搜索过程向最优解逼近.
设优化问题为对图2所示的稀布线阵,阵元数为M,固定第1个阵元位于原点位置 (x1=0),则只需要对M-1 个阵元间距(d1,d2,…,dM-1)进行优化,其中最小阵元间距为dlb,最大阵元间距为dub,使得该阵所形成的近场方向图在期望方向与期望距离的PSLL最低,即
(5)
其中,P表示稀布阵列天线方向图的PSLL.
2.1 种群初始化及参数设置
此时的待优化变量个数为M-1,由于第1个阵元位置给定(x1=0),则稀布阵列内所有阵元位置xm可表示为
(6)
文中在仿真实验中选取的种群规模为4(M-1),差分尺度因子F=0.5,交叉概率RC= 0.9.
2.2 适应度函数的选取
选取期望方向θ0所在距离方向图的第1副瓣与期望距离r0所在的方位方向图的第1副瓣的最小值作为适应度函数.由于近场阵列流形自身表达式的原因,所产生的聚焦波束不一定会在期望位置(r0,θ0)形成最大值,此时需要对适应度函数加上一个罚函数,如果优化的个体无法在期望位置(r0,θ0)产生最大值或较大值,则将此个体剔除,其表达式为
f(n)=min (Pθ0,Pr0)+p,
(7)
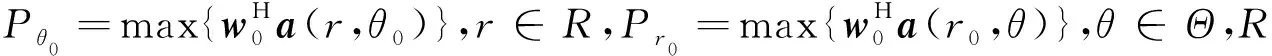
2.3 算法步骤
算法的步骤如下:
(1) 设置基本参数: 尺度因子F,交叉概率(RC)以及种群规模(PN).
(2) 设置代数G=0,初始化种群PG,其中每个个体向量均匀分布在给定的上下界范围内.
(3) 计算种群(PN)个体的适应度值.
(4) 判断优化准则是否满足,若已满足,则转最后一步;否则,继续.
(5) 差分进化算法.
(6) 输出最佳个体,结束.
3 实验仿真与分析
为了验证算法的有效性,对稀布阵列天线的近场波束综合进行了仿真实验.仿真过程中假设稀布阵列天线阵元为理想化的各向同性天线,在实际稀疏阵列天线近场综合问题中,认为满足远场情况下稀疏阵列天线综合的单元天线同样可以满足近场天线综合的要求,诸如微带天线,加载反射板的偶极子天线等定向天线单元均可使用,只要保证天线单元的辐射范围包含稀布阵列天线综合的覆盖范围即可.其他仿真实验参数设计如表1所示.

表1 实验仿真参数

图3 阵型优化后的三维方向图
仿真实验1 进行20阵元的稀疏线阵的近场波束综合设计,约束阵元间距为 0.5λ 图3为对稀布阵列天线的阵元位置进行优化后得到的三维波束方向图.图4为阵元位置优化后与采用相同阵元间距约束的均匀稀布阵列以及相同稀布阵列孔径下间距随机的稀布阵列对比的仿真结果图,其中横线表示文中算法优化后的PSLL.从图4可以看出,在当前阵元间距约束条件下,波束方向图无栅瓣,PSLL可以认为是第1副瓣的幅度,通过DE算法进行稀布阵列位置优化后,PSLL显著降低,降低幅度为 7 dB 左右,但会带来主瓣区域的展宽,大约展宽为0.6°.3种布阵方式对于距离维方向图影响不大,均可以在期望距离形成主瓣,且主瓣展宽不明显.由此可以说明,DE算法进行稀布线阵位置优化后对PSLL抑制效果明显,且对主瓣区域影响不大. 图4 不同布阵情况下方向图结果对比 仿真实验2 将其他仿真实验参数与仿真实验1保持一致,调整天线单元之间的间距,分别取 0.5λ 图5为不同阵元间距约束下文中算法的仿真结果图.从图5可以看出,当约束的阵元间距变大时,聚焦的主瓣变窄,主瓣区域减少约1.8°,但由于阵元间距拉大引入的栅瓣效应,阵元间距约束为 1λ 图5 不同间距约束条件下方向图结果对比 文中对近场电磁波传播模型的传播时延原始表达式进行了分析,提出了一种用于稀布阵列的近场波束综合算法.采用DE算法,在给定阵元数目、不同阵元间距约束的情况下,实现了在较高稀疏率情况下的近场聚焦波束修正和峰值旁瓣电平控制,并通过仿真验证了算法的可行性与有效性.同时,文中提出的算法同样可以扩展到二维面阵甚至三维立体阵,但随之而来的是更高的运算复杂度.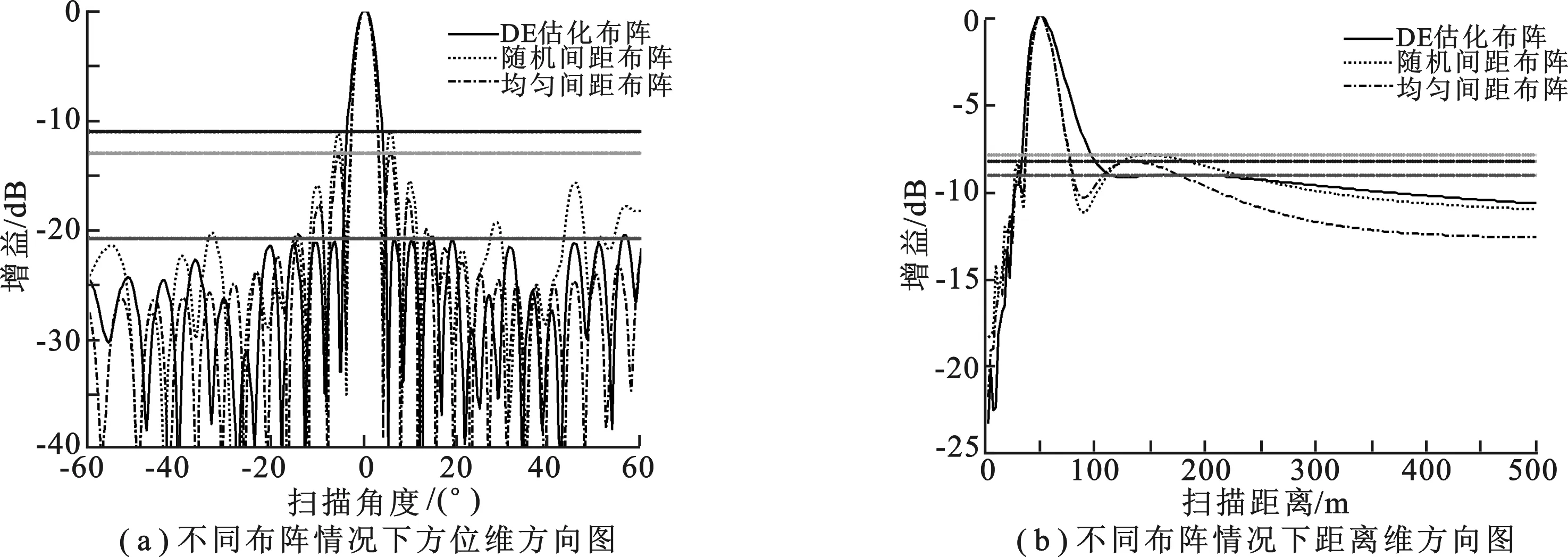

4 结 束 语
