并行区域分解法分析千波长目标散射特性
2018-12-07顾宗静林中朝赵勋旺
苏 秦,顾宗静,林中朝,赵勋旺,张 玉
(西安电子科技大学 天线与微波技术重点实验室,陕西 西安 710071)
雷达散射截面(Radar Cross Section,RCS)的计算是伴随着雷达目标的检测和识别技术发展起来的,它不仅可以应用于现有的各种目标,又可以用来预估和优化未来的信息化系统,在工程应用领域具有重要作用.尤其是近几十年来,隐身技术与精确目标识别技术日新月异,这对电大尺寸复杂目标的RCS计算提出了更高的要求.对于电尺寸很大的散射体,通常采用物理光学法(Physical Optics method,PO)等高频算法求解,然而,高频算法难以保证足够的精度.传统的高精度电磁场数值算法如矩量法(Method of Moment,MoM)和有限元等算法往往只能解决几十个波长的电磁问题.多层快速多极子算法(MultiLevel Fast Multipole Algorithm,MLFMA)的求解规模可以达到上百波长[1],但对于上千波长规模的问题在资源有限的情况下仍然很难求解.这迫使人们必须找到一种高效可实现的数值仿真方法.
区域分解方法(Domain Decomposition Methods,DDM)是使用“分而治之”的思想解决问题的方法.它先对整体目标进行分区,依据其物理或电磁散射特性划分为多个子区域独立求解,然后通过考虑子区域间的耦合关系,最终得到原问题的解.由于每个子区域处于独立求解空间,并且具有相对较少的未知量,这就使得大型电磁仿真分析的快速实现成为可能.在有限元与有限差分领域,DDM已经成功实现[2-3].而在积分方程领域,如MoM,近年来对于DDM的研究也越来越受到学者们的关注.一种广泛采用的重叠型DDM中[4],相邻两个子区域间存在重叠部分,这种方法可以使得电磁流更加逼近真实电磁流.但是重叠区的引入给建模带来了不便,同时区域延伸也导致了计算量增加.而另一种非重叠型DDM则是在子区域之间引入人工虚拟面,将原问题分解为很多闭合的子区,每次迭代通过修正虚拟面上电磁流来保证相邻子区域场的连续性[5].这种方法节省了几何建模的工作量,具有较高的灵活性.然而对于用区域分解方法解决千波长规模电磁问题,鲜有有效工作内容发表.这主要是因为DDM的并行方案复杂,并且在计算电大尺寸问题时,为了保证足够的精度,通常需要用MLFMA来降低内存消耗与计算复杂度,而MLFMA的八叉树结构,使得其在并行化过程中的负载均衡难以实现.
针对这一问题,文中给出一种高效的基于积分方程的并行非重叠区域分解方法(Integral Equation-based Nonoverlapping Domain Decomposition Method,IE-NDDM).与文献[6]中所有子区域同时计算的并行方案相比,并行IE-NDDM将所有计算机资源集中对单个子区域求解,避免了子区域大小划分不均等所导致的负载不均衡,同时待求解问题的规模也大大提升.每个子区域内部以及子区域间耦合量的求解均用并行MLFMA进行加速.改进的平面波自适应划分策略使得并行MLFMA的数据划分更加均衡,进一步提高了并行IE-NDDM的计算能力和效率.子区域间的耦合量计算采用场迭代的方式,降低了计算过程中的内存消耗.文中最后给出一个实际应用中的千波长舰船的散射特性分析,数值结果表明,该方法能够有效应用于电大尺寸散射体的快速精确仿真.
1 IE-NDDM原理
与重叠型DDM相比,IE-NDDM仅在相邻子区域切割处增加虚拟面,使各个子区域封闭.此处以金属目标划分为两个非重叠型子区域为例进行分析,对于多个子区域情况可以依此类推.
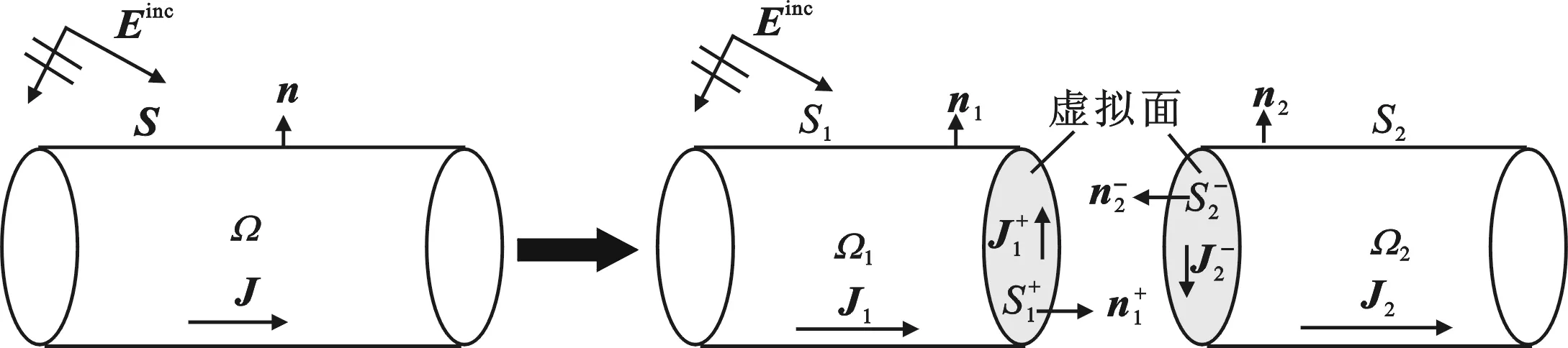
图1 模型区域分解示意图

以子区域Ω1为例,在平面波{Einc,Hinc}入射时,根据等效原理,其表面电场积分方程(Electric Field Integral Equation,EFIE)及磁场积分方程(Magnetic Field Integral Equation,MFIE)可以写为
(1)
其中,{Es,Hs}代表金属体表面等效源所产生的散射场.对于金属体表面而言,只有电流J,因此,散射场用等效源的积分形式可以表示为
(2)
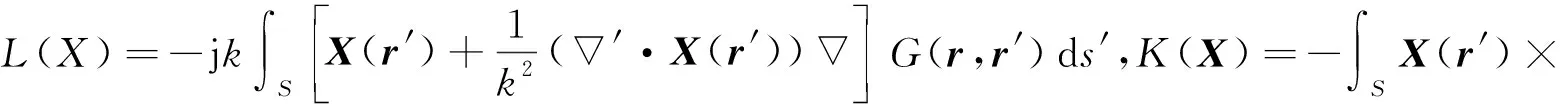
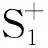
(3)
2 IE-NDDM的并行策略
对式(1)中的EFIE及MFIE线性组合起来得到混合场积分方程(Combined Field Integral Equation,CFIE),并用伽辽金匹配来构建出全局矩阵方程.对于n个子区域,方程ZI=V可以写成如下形式:
(4)
其中,当i=j时,Zij为第i个子区域Ωi的自阻抗矩阵; 当i≠j时,Zij为子区域Ωj和子区域Ωi的互阻抗矩阵;Ii为子区域Ωi的电磁流系数矩阵,Vi为子区域Ωi的电压矩阵.

(5)
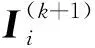
(6)
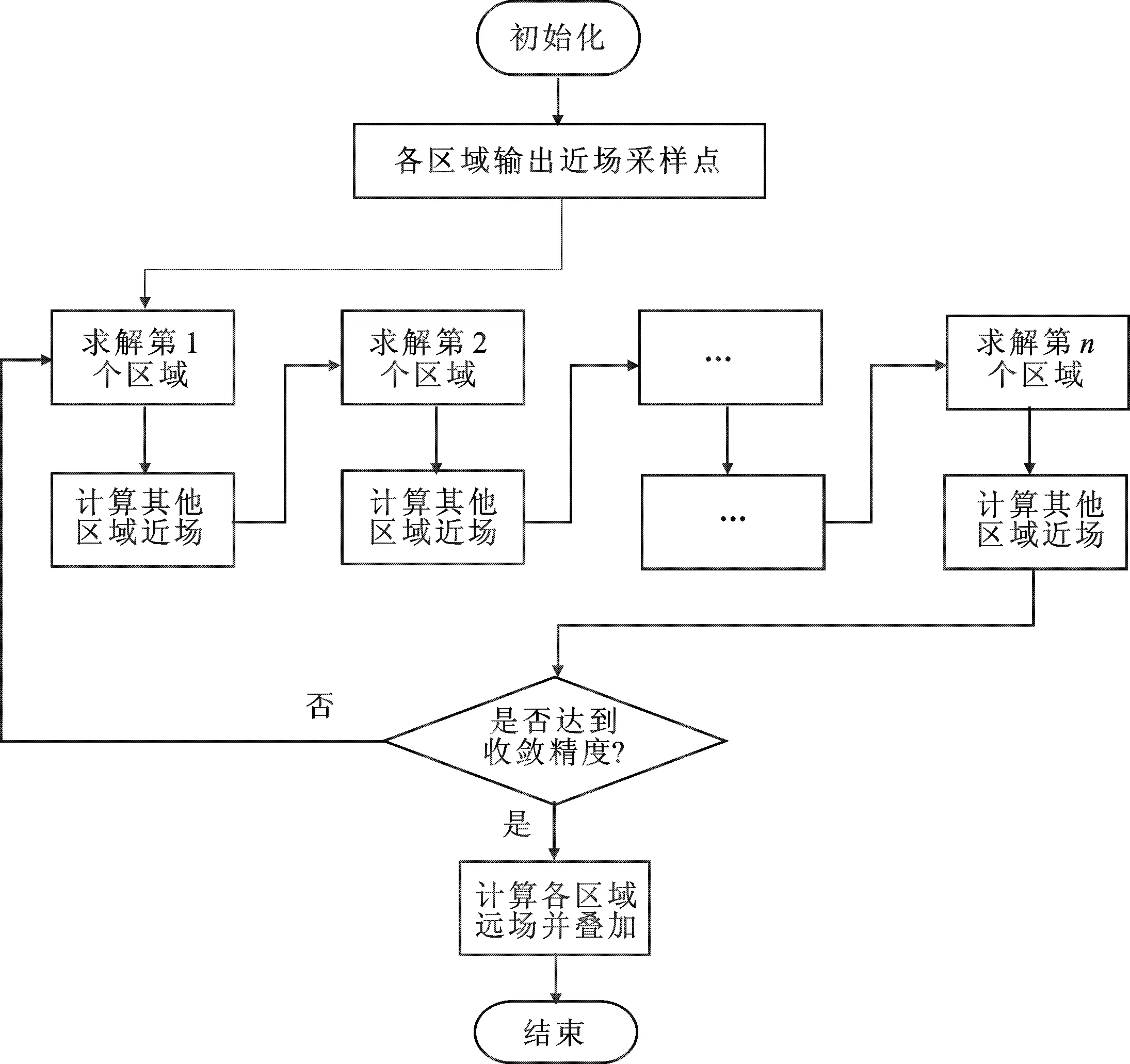
图2 并行IE-NDDM外迭代流程图
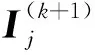
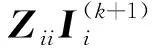
MLFMA有两种基本并行策略,分别是组划分与平面波划分策略.如果只使用组划分策略,那么在高层会存在瓶颈,因为高层的非空组较少,无法分配给较多的并行进程.同理,如果只使用平面波划分策略,那么在低层存在瓶颈.为了提高并行MLFMA的可扩展性,需要混合使用这两种并行策略.比较简单的混合策略是在低层采用组划分,在高层采用平面波划分,通过设置中间过渡层实现两种策略的结合.然而在过渡层,非空组数和每个非空组对应的平面波数均为O(N0.5).当进程数超过O(N0.5)时,该混合策略在过渡层出现瓶颈.为了解决过渡层的瓶颈,一种逐层渐变划分策略(HiP)将组划分与平面波划分策略紧密结合,具有较高并行效率[8].在此基础上,文中对MLFMA采用一种改进的平面波自适应划分(Adaptive Partition,AdP)并行策略[9],并行编程模型为基于分布式内存的消息传递接口(Message Passing Interface,MPI).该策略同样采用逐层渐变的方式对平面波方向进行划分.不同的是,在某一层对于不同的非空组,HiP对于平面波划分的份数相同,而AdP根据非空组所在的进程数进行自适应划分,非空组所在的进程数不同则平面波划分份数也随之不同.设并行进程数为Np,将基函数(或权函数)等分为Np个部分,每部分基函数被分配给一个进程.然后,每个进程根据所分配到的基函数建立相应的子树.如图3(a)所示,第2层至第4层的八叉树被分配到6个进程中,其中进程编号记为P0~P5,非空组中标注的进程编号就是该非空组所在的进程.对于图3(a)中的第3层,该层中的3个非空组分别存在于1个、2个、3个进程中.每个非空组对应的外向平面波和内向平面波被均等地分配到其所在的进程中.图3(b)所示为图3(a)中第2层非空组的平面波划分示意图,每个圆点代表一个平面波方向.

图3 八叉树的数据划分
这种准二维划分的AdP对使用的进程个数无特殊要求,组划分与平面波划分无缝结合.每个进程都参与计算和通信,这使得各个进程中的通信量和计算量更加均衡.在聚合-转移-配置(MVP)过程中,向上聚合与向下配置时,进程中外向平面波和内向平面波的交换和叠加都在缓冲区中进行,避免了插值过程中的通信.同时,利用MPI中的非阻塞通信技术,将进程内计算与进程间通信相互重叠,进一步提升了MLFMA的并行效率,这使得并行IE-NDDM在普通工作站上即可快速求解大规模电磁问题.关于AdP的大规模并行性能详见文献[9].
3 数值算例
3.1 波音737飞机的散射特性
此处以波音737飞机的散射特性为例来证明并行IE-NDDM算法的正确性与高效性. 入射波面向机头入射,极化方向为 +z.飞机模型划分为5个子区域,如图4(a)所示,其尺寸为 30.6 m× 29.0 m× 11.7 m.当入射波频率为 1 GHz 时,表1列出了两种计算方式消耗的计算资源和计算时间.可以看出,并行IE-NDDM与FEKO整体解相比,内存使用峰值降低86.7%,同样使用16个CPU核数时,总计算时间也缩短了36.1%.图4(c)~图4(d)中实线为并行IE-NDDM数值计算结果,虚线为商业软件FEKO用MLFMA整体求解的仿真结果,图4(b)为并行IE-NDDM算法外迭代收敛曲线.可以看出,文中提出的并行IE-NDDM算法4步迭代收敛精度已达到 0.002 63,并且与整体解的结果曲线吻合良好,尤其在前后向几乎完全重合.从而证明了并行IE-NDDM算法的准确性,为计算更大规模的散射体提供了理论支持.图4(c)和图4(d)中同时给出了并行IE-NDDM计算得到的入射波频率为 10 GHz 时飞机的RCS,此时飞机的电尺寸达到 1 000 波长.

表1 频率为1 GHz时的计算资源列表
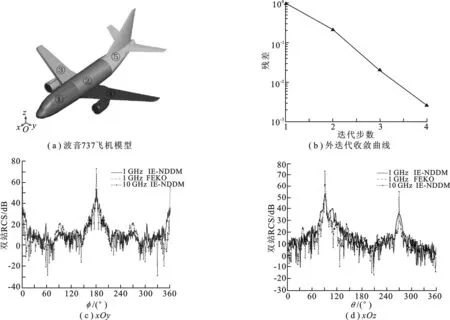
图4 飞机模型及其RCS
3.2 舰船的散射特性分析
此处以舰船模型为例,用并行IE-NDDM算法对其散射特性进行计算.该舰船模型如图5(a)所示,其尺寸为 153.0 m× 16.5 m× 28.0 m,共划分为7个子区域.入射方向为面向船头入射,极化方向为 +z.外迭代收敛残差设为0.01.当入射波的频率为 300 MHz 时,舰船的RCS计算结果如图5(b)~图5(c)所示.可以看出,对于该模型并行IE-NDDM与整体解的结果曲线依然吻合良好.当入射波的频率为 2 GHz 时,相应的电尺寸为 1 020λ× 110λ× 186.7λ.对整体模型剖分所产生的未知量个数为 66 171 474,此时用现有计算机资源已很难得到整体解.采用并行IE-NDDM算法求解,最大的子区域未知量个数为 14 813 784,用32个CPU核进行计算,总耗时为 19.2 h.同时,占用的总内存峰值仅为 105.6 GB.这表明在计算资源有限时,该并行IE-NDDM算法在计算时间和资源消耗上都拥有极大优势.此时舰船的RCS计算结果如图6(a)~图6(b)所示.
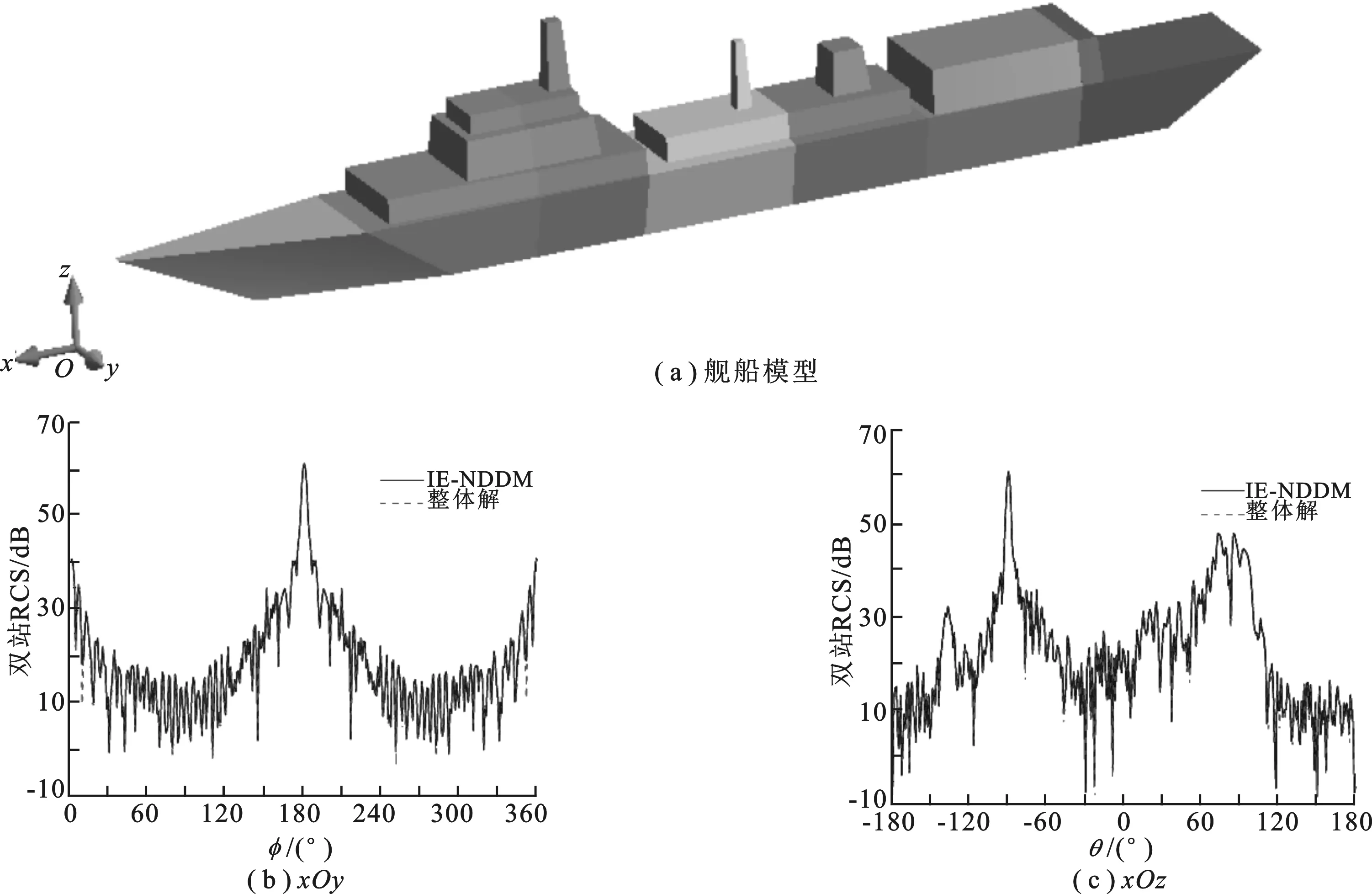
图5 舰船模型以及在300 MHz时的RCS
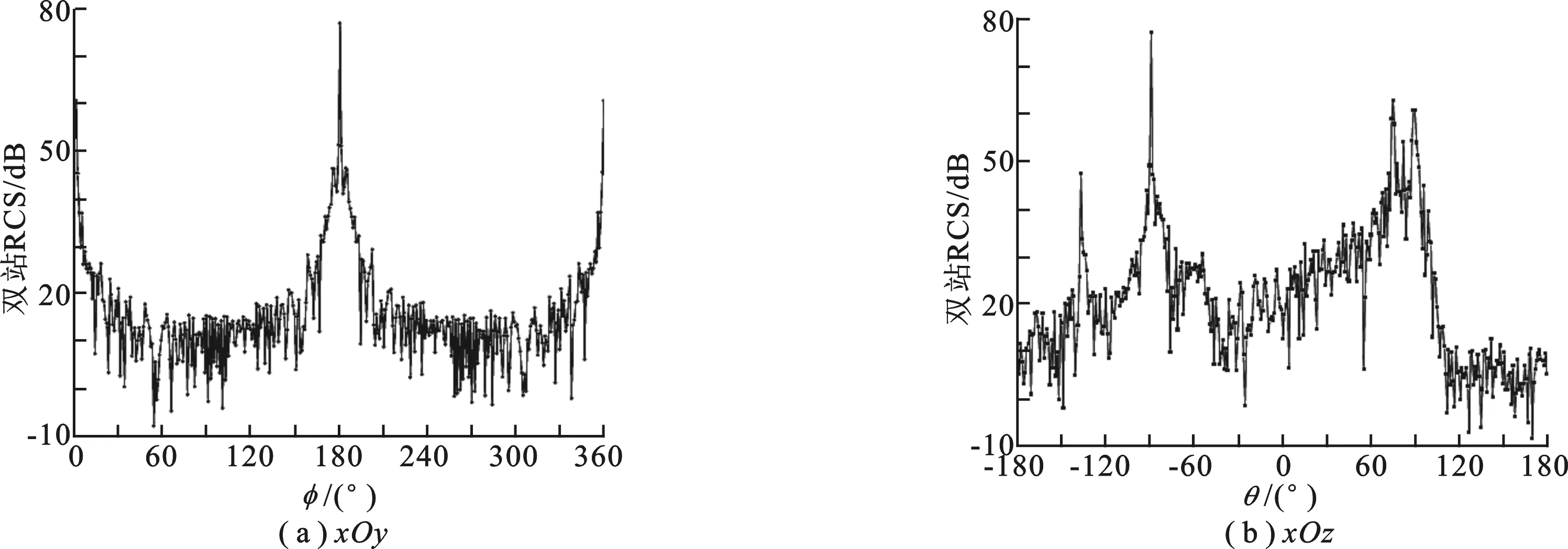
图6 舰船在2 GHz时的RCS
4 结 论
在非重叠型区域分解法的基础上,采用并行多层快速多极子对子区域内部以及子区域间耦合的计算进行加速.改进的自适应划分并行策略提高了多层快速多极子的并行效率,子区域间耦合计算用场迭代的方式降低了内存.这使得电大尺寸电磁问题的精确高效求解成为可能,在资源有限的情况下,千波长目标散射特性计算的工程难题得到了解决.下一步尝试将天线加载到电大尺寸平台上,解决更加复杂的电磁仿真问题.
