聚焦数学思想培养的小学数学课堂研究

董旭妹

摘 要：数学思想是数学的灵魂，教师在备课中探寻数学思想，在课堂的探究过程中巧妙渗透数学思想，让学生领会数学思想的妙用，把握数学学习的灵魂。结合笔者的实际教学，就小学数学课堂数学思想的培养作浅显探索。

关键词：数学思想；渗透；课程

《义务教育数学课程标准》（以下简称《标准》）中指出：“课程内容既要反映社会的需要、数学学科的特征，也要符合学生的认知规律。它不仅包括数学的结论，也应包括数学结论的形成过程和数学思想方法。”《标准》已将数学基本思想纳入义务教育阶段的数学学习目标，所以，教师要领悟“标准”的变化，从思想上提高对数学思想渗透重要性的认识，在课堂中把握课堂环节，适当渗透数学思想，使得学生知识和思想方法的双丰收。

一、渗透数学思想，有序导入新课

“引入环节”是一节完整课堂教学不可缺少的环节，它犹如电影的“序幕”，对于新授环节的教学有着重要的作用。

1.无声转化，旧知引新知

课伊始，教师可以抓住新旧知识之间的联系，创设合理的情境，让学生在搭建知识建构的桥梁中，进行合理的迁移、转化，进而进入新知识的探究中去。在学习“三角形的面积”前，教师可以请学生回忆之前学习过哪些图形的面积，让学生在复习平行四边形的面积后，想一想三角形能否转化为平行四边形，使学生在三角形和平行四边形之间建构桥梁。

2.数形、分类，概念教学更畅通

小学阶段学生是以形象思维为主，认知水平不高，他们的思维离不开生活中具体事物。在学习“方程”时，我们首先让学生观察演示天平上左右两盘的物体，将形象的事物用抽象的算式表示；然后再请学生将汇总的算式进行分类（按照是等式还是不等式分一分，并在后面标注出是否含有字母）。让学生在数形思想和分类思想的引导下，对这些算式有了一定的认识，为后面方程概念的总结提供了有力的证据。

二、渗透数学思想，精彩探究新知

数学是知识和思想方法的有机融合，在课堂教学中，教师要注意找到两者之间的联系，在学生探究知识的过程中，适时渗透数学思想方法，使学生感受数学思想在具体问题中的存在，感知数学思想在解决问题中的意义。

1.渗透符号化思想

符号化思想主要是指运用符号去表达研究的对象，恰当的符号可以清晰地表示出数学概念和事物之间的逻辑关系等。符号化思想在小学数学内容中随处可见。在教学“平行四边形的面积”时，学生通过剪拼，发现平行四边形和长方形的联系，总结出平行四边形的面积=底×高，把面积公式变成符号化的语言就是S=ah，明确a、h表示的意义，知道用符号化的语言表示这类公式更简洁，从而使学生了解、建立符号化思想。

2.渗透统计的思想

“统计”就是搜集、整理、计算和分析有关研究对象的数据，制作相应的表格、图形，并作出适当的推断。在学习“可能性”时，让学生抛硬币，统计出现正面和背面的次数；学习“平均数”时请学生统计本班学生的身高和体重，填写统计表；学习“扇形统计图”时让学生统计本班学生爱好，制作统计图……以上都是在渗透统计的数学思想。

3.渗透对应、极限思想

“对应”反映的是两个集合的元素间的关系。一年级教学“多与少”时，教师可以出示生动直观的动物卡片：上面是4只小鸡，下面是3只小兔子，问“哪种动物多”，引导学生将两种动物一一对应，发现小鸡还多着一只，所以小鸡多。就这样，学生在比较的过程中感受一一对应。

在“认识自然数”中，在数轴上标注出一个一个的点，并在点处标注上0、1、2、3……让学生从一一对应的点和数中发现：自然数都能用数轴上一个一个的点表示，没有最大的自然数，自然数无限多……对应、极限思想无形中渗透到课堂中。

4.渗透数形结合的思想

数形结合思想方法是指将数与式的代数信息和点与形的几何信息互相转换。“数缺形时少直观，形少数时难入微。”这句话足以证明“数形结合”在数学中的重要地位。

在教学“有余数的除法”过程中，教师可以让学生拿出自己的学具小棒，动手分摆，根据摆分的结果列出相应的算式。用生活中的实际事物，帮助学生理解除法算式中的平均分的过程，就这样，“数”在实实在在的“形”中得到理解，问题在“形”的摆分中得到解决。

三、渗透数学思想，让练习效果斐然

数学知识的巩固，技能的形成，智力的开发，能力的培养等需要适量的练习才能实现。学生数学思想方法是否掌握，需要学生在练习中进行验证。

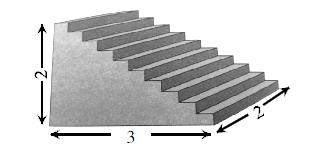
在学习了“平行四边形”后的练习中，有一题目：楼梯台阶上铺着地毯（如下图），你能计算出最少需要多少平方米的地毯吗？这道练习需要用转化思想将图形进行变形，得到地毯的长其实就是台阶侧面的一个长和一个高的总和。讲解时，教师要在圖中进行线段的平移，将转化的过程进行详细地演示，让学生真正明白地毯的长究竟为什么是5米，将转化思想内化于心。

思想是数学的灵魂，不管是概念的建立、数学公式的发现，还是数学问题的解决，核心在于数学思想方法的渗透和建立。在新课改的要求之下，教师也要在教学理念和教法上进行改变，深研教材，提高思想方法渗透的自觉性，让学生的数学思维能力得到切实有效的发展，从而提高学生的数学素养。

参考文献：

杨庆余.小学数学课程与教学[M].高等教育出版社，2004.