六种方法助力 数列求和省力

福建 汤小梅

数列求和是新课标高考的一个必考的重点和热点，多为解答题，有时也以选择题或填空题的形式呈现，多为中档题，主要考查考生的逻辑推理、数学运算等核心素养．现走近2018年高考题与各省市质检题，借“题”发挥，挖掘数列求和题的六种方法，让您对数列求和的命题角度与应对方法宏观把握、了然于胸．

命题角度1 用公式法求数列的和

【典例1】(2018·全国卷Ⅱ·理17文17)记Sn为等差数列{an}的前n项和，已知a1=-7，S3=-15．

(1)求{an}的通项公式；

(2)求Sn，并求Sn的最小值．

【点睛】先设{an}的公差为d，利用等差数列的通项公式，得d的方程，解方程，求出d的值，从而得{an}的通项公式；(2)利用(1)与等差数列的前n项和的公式，求出Sn，再利用配方法，即可求出Sn的最小值.

【解】(1)设{an}的公差为d，由题意得S3=3a1+3d=-15，

又a1=-7，解得d=2.

所以{an}的通项公式为an=2n-9.

(2)由(1)得Sn=n2-8n=(n-4)2-16.所以当n=4时,Sn取得最小值,最小值为-16.

【解题技巧】破解此类题只需双招，第一招：公式关，等差数列的5个基本量a1,d,an,n,Sn，一般可以“知三求二”，通过等差数列的通项公式与前n项和的公式，列出方程(组)，即可求出所需求得的量；第二招：配方关，即会利用配方法求等差数列前n项和的最值．

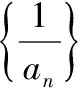
命题角度2 用裂项相消法求数列的和

【典例2】(2018·广东省六校高三第二次联考·理17)已知数列{an}为等差数列，Sn为其前n项和，且a2=4,S5=30，数列{bn}满足b1+2b2+…+nbn=an.

(1)求数列{an}的通项公式；

(2)设cn=bnbn+1，求数列{cn}的前n项和Tn.

【点睛】(1)设数列{an}的公差为d，利用等差数列的通项公式与前n项和的公式，得a1,d的方程组，解方程组，求出a1,d的值，即可得数列{an}的通项公式；(2)先求出数列{bn}的通项公式，再求数列{cn}的通项公式，利用裂项相消法，即可求出数列{cn}的前n项和Tn.

解得a1=2,d=2，故数列{an}的通项公式为an=2+2(n-1)=2n.

(2)由(1)可得b1+2b2+…+nbn=2n①，

所以当n≥2时，

b1+2b2+…+(n-1)bn-1=2(n-1) ②，

【解题技巧】求解此类题需过“双关”：一是通项关，即会利用求通项的常见方法，求出数列的通项公式；二巧裂项关，数列的通项公式准确裂项，表示为两项之差的形式；三是消项求和，即把握消项的规律，求和时正负项相消，只剩下首末若干项，达到准确求和．

【变式训练2】(2018·漳州市5月高三质检)已知数列{an}的前n项和为Sn，满足S2=2，S4=16，{an+1}是等比数列.

(1)求数列{an}的通项公式；

【解】(1)设等比数列{an+1}的公比为q，其前n项和为Tn，

因为S2=2，S4=16， 则T2=4，T4=20，

命题角度3 用分组求和法求数列的和

将一个数列分成若干个简单数列(如等差数列、等比数列、常数列等)，然后分别求和.也可先将数列通项拆开，看成等差或等比的加减运算形式，再分组求和，即把一个通项拆成几个通项的形式，方便求和.

【典例3】(2018·天津卷·理18) 设{an}是等比数列，公比大于0，其前n项和为Sn(n∈N*)，{bn}是等差数列. 已知a1=1，a3=a2+2，a4=b3+b5，a5=b4+2b6.

(1)求{an}和{bn}的通项公式；

(2)设数列{Sn}的前n项和为Tn(n∈N*)，

(ⅰ)求Tn；

【解】(1)设等比数列{an}的公比为q.

由a1=1,a3=a2+2,可得q2-q-2=0.

因为q>0，可得q=2，故an=2n-1.

设等差数列{bn}的公差为d，由a4=b3+b5，可得b1+3d=4.

由a5=b4+2b6，可得3b1+13d=16, 从而b1=1,d=1, 故bn=n.

所以数列{an}的通项公式为an=2n-1，数列{bn}的通项公式为bn=n.

【解题技巧】破解此类题的关键：一是活用“基本量法”，若干个能唯一确定一个数列的量称为该数列的“基本量”.首项与公差是等差数列的“基本量”，首项与公比是等比数列的“基本量”，在解决等差数列或等比数列的相关问题时，常用等差(等比)的通项公式及其前n项和的公式；二是活用公式法、分组求和法与裂项相消法求数列的前n项和．

【变式训练3】已知等差数列{an}的首项为a，公差为d，且不等式ax2-3x+2<0的解集为(1,d)．

(1) 求数列{an}的通项公式an；

(2)若bn=3an+an-1，求数列{bn}前n项和Tn．

(2)由(1)知bn=32n-1+2n-1-1,

∴Tn=(3+1)+(33+3)+…+(32n-1+2n-1)-n

=(31+33+…+32n-1)+(1+3+…+2n-1)-n

命题角度4 用错位相减法求数列的和

错位相减法是指已知数列{an}是等差数列，数列{bn}是等比数列，求数列{anbn}的前n项和Sn时，先对Sn乘以等比数列{bn}的公比，再错开位置，把两个等式进行相减，从而求出Sn的方法．错位相减法是所有求和方法中最重要的方法之一，也是高考的热点．应用时需小心：相减时注意最后一项的符号；用等比数列的前n项和的公式求和时注意项数别出错．

(1)求an；

【点睛】(1)设等差数列{an}的公差为d，利用等差数列的前n项和的公式与通项公式，即可求出d，从而求出an；(2)利用(1)的结论，求出bn的通项公式，再利用错位相减法求Tn.

【解】(1)设等差数列{an}的公差为d，

所以a10-a5=10,所以5d=10，解得d=2.所以an=a1+(n-1)d=2+(n-1)×2=2n；

所以Tn=1×23+2×24+3×25+…+n·2n+2①，

所以2Tn= 1×24+2×25+3×26+…(n-1)·2n+2+n·2n+3②，

所以Tn=(n-1)×2n+3+8.

【解题技巧】运用错位相减法求和的关键：一是判断模型，即判断数列{an}，{bn}一个为等差数列，一个为等比数列；二是错开位置，如【典例3】的“②”式，先乘以公比2，再把前n项和退后一个位置来书写，这样为两式相减不会看错列做准备；三是相减，相减时定要注意“②”式中的最后一项的符号，学生常在此步出错，定要小心．

(1)求数列{an}的通项公式；

当n=1时，4S1=(a1+1)2，得a1=1．

当n≥2时，4Sn-1=(an-1+1)2，

∴4(Sn-Sn-1)=(an+1)2-(an-1+1)2，

∴4an=an2+2an-an-12-2an-1，

即(an+an-1)(an-an-1)=2(an+an-1)，

∵an>0,∴an-an-1=2．

∴数列{an}是等差数列，且首项为a1=1，公差为2，

∴an=1+2(n-1)=2n-1．

命题角度5 用并项求和法求数列的和

用并项求和法求数列的和是指把数列的一些项合并组成我们熟悉的等差数列或等比数列来求和. 并项求和法常见类型：一是数列的通项公式中含有绝对值符号；二是数列通项公式中含有符号因子“(-1)n”．

【点睛】由三角函数的特征，对n进行分类讨论，再利用并项求和法，求出{an}的前100项和．

【解】设k∈N*,(1)当n=2k时，a2k+1=-a2k+4k，即a2k+1+a2k=4k；

(2)当n=2k-1时，a2k=a2k-1+4k-2；

联立(1) (2)可得，a2k+1+a2k-1=2,所以数列{an}的前100项和为

S100=a1+a2+a3+a4…+a99+a100

=(a1+a3+…+a99)+(a2+a4+…+a100)

=(a1+a3+…+a99)+[(-a3+4)+(-a5+4×2)+(-a7+4×3)+…+(-a101+4×50)]

=25×2+[-(a3+a5+…+a101)+4×(1+2+3+…+50)]

=5 100.

【变式训练5】已知数列{an}满足an+1=(-1)n(3an-1+1)+1,n≥2，且a1=a2=1，则数列{an}的前2 019项的和为 .

【解】①当n=2k,k∈N*时，

a2k+1-1=3a2k-1+1,

∴a2k+1=3a2k-1+2，

∴a2k+1+1=3(a2k-1+1)，

所以{a2k-1}是首项为2，公比为3的等比数列，

∴a2k-1=2×3k-1-1.

②当n=2k+1,k∈N*时，a2k+2-1=-(3a2k+1),

∴a2k+2=-3a2k，

所以a2k是首项为1，公比为-3的等比数列，

∴a2k=(-3)k-1.

∴S2019=(a1+a3+…+a2019)+(a2+a4+…+a2018)

=[(2×30-1)+(2×31-1)+…+(2×31009-1)]+[1+(-3)+…+(-3)1008]

命题角度6 倒序相加法

倒序相加法是指已知数列特征是“与首末两端等距离的两项之和相等”，先把数列求和的式子倒过来写，然后对两个求和的式子进行相加，即可求出该数列的前n项的和的方法．

【典例6】已知正实数x,y满足lgx+lgy=12，且Sn=lgxn+lg(xn-1y)+lg(xn-2y2)+…+lg(xyn-1)+lgyn，则Sn= ．

【点睛】利用对数的运算法则，先化简已知等式，再利用倒序相加法，即可求出Sn．

【解】∵lgx+lgy=12，∴lg(xy)=12，

∵Sn=lgxn+lg(xn-1y)+lg(xn-2y2)+…+lg(xyn-1)+lgyn，

∴Sn=lgyn+lg(xyn-1)+…+lg(xn-2y2)+lg(xn-1y)+lgxn，

以上两式相加得，

2Sn=(lgxn+lgyn)+[lg(xn-1y)+lg(xyn-1)]+…+(lgyn+lgxn)

=lg(xn·yn)+lg(xn-1y·xyn-1)+…+lg(yn·xn)

=n[lg(xy)+lg(xy)+…+lg(xy)]

=n[(n+1)lg(xy)]=12n(n+1)，

所以Sn=6n(n+1)．

【解题技巧】破解此类求数列的前n项和题的关键：一是会观察数列的特点，观察数列前后是否具有“对称性”，若是，则采用倒序相加法求这个数列的前n项和；二是熟练运用对数的运算法则进行计算；三是需注意：倒序后，对两式相加，得出的式子出错，如本例题，两式相加后误得，Sn=(lgxn+lgyn)+[lg(xn-1y)+lg(xyn-1)]+…+(lgyn+lgxn)，左边式子漏掉了2倍，应给予警惕，不要因这类低级的错误而失分．

【变式训练6】已知log5m,log5t(m,t∈R+)为关于x的方程x2-25x+λ=0的两个不同的实根，且Sn=log5mn+log5(mn-1t)+log5(mn-2t2)+…+log5(mtn-1)+log5tn，则Sn= ．

【解】∵log5m,log5t(m,t∈R+)为关于x的方程x2-25x+λ=0的两个不同的实根，

∴log5m+log5t=25，

∴log5(mt)=25，

∵Sn=log5mn+log5(mn-1t)+log5(mn-2t2)+…+log5(mtn-1)+log5tn，

∴Sn=log5tn+log5(mtn-1)+…+log5(mn-2t2)+log5(mn-1t)+log5mn，

以上两式相加得

2Sn=(log5mn+log5tn)+[log5(mn-1t)+log5(mtn-1)]+…+(log5tn+log5mn)

=log5(mn·tn)+log5(mn-1t·mtn-1)+…+log5(tn·mn)

=n[log5(mt)+log5(mt)+…+log5(mt)]

=n(n+1)log5(mt)=25n(n+1)，