应用分组法求解数列中的“出”与“入”
2018-12-06江苏王安寓
江苏 王安寓
将数插入一个数列中,或将两个数列相互嵌入,是数列命题的常用手段;将一个数列中的部分项舍去,构造新的数列,是数列命题的另一手段.通过数列的“入”——吞噬与“出”——舍弃,改变数列的原有规律,缔造数列新秩序,增加思维度和计算量,同时也增加难度.
一、数列中的“入”
数列作为6大模块之一,其地位相当重要.在各种考试中,对数列的考查都是重中之重,特别是江苏、浙江、天津等省.对数列的命题,每年都会推陈出新.命题的手段主要集中在数列的基本量计算和新数列的构造.而构造新数列的手段很多,常见的有两个数列的相互嵌入与一个数列的部分项的删除.
1.1 两个数列的相互嵌入
题目1(2018·江苏卷·14)已知集合A={x|x=2n-1,n∈N*},B={x|x=2n,n∈N*}.将A∪B的所有元素从小到大依次排列构成一个数列{an}.记Sn为数列{an}的前n项和,则使得Sn>12an+1成立的n的最小值为________.
【分析】集合A的元素按照从小到大的顺序排列,构成等差数列An=2n-1,集合B的元素按照从小到大的顺序排列,构成等比数列Bn=2n,它们没有公共元素,则数列{an}是将数列Bn=2n插入到数列An=2n-1中,或者是将数列An=2n-1插入到数列Bn=2n中构造而成.考虑数列An=2n-1插入到数列Bn=2n中,则插入规律是:在Bk-1与Bk之间插入2k-1+1,2k-1+3,…,2k-1,计2k-2个数,如何求数列{an}的前n项和Sn呢?数列{an}的规律并不明显:既不是等差数列,也不是等比数列,通项公式不易写出.但运用分组:(1,2),(3,4),(5,7,8),(9,11,13,15,16),(17,19,…,32),…,(2k-1+1,2k-1+3,…,2k),就能看出前n项和的规律.抓住这个分组,就能把Sn的表达式写出,从而完成不等式Sn>12an+1的求解.
【解析】(分组法求和):记{an}中第k组为(2k-1+1,2k-1+3,…,2k),记An=2n-1,Bn=2n,则{an}中第k组含有An计2k-2个,Bn计1个,其和为3·4k-2+Bk,前k组含有An计1+1+2+…+2k-2=2k-1个,Bn计k个,其和为4k-1+2k+1-2,
∴当n=1时,S1=1,a2=2,Sn>12an+1不成立;
当n=2k-1+k,k∈N*时,Sn=4k-1+2k+1-2,an+1=2k+1,

∴k>5.
当n=2k-1+k+m,k∈N*,m≤2k-2,m∈N*时,Sn=(2k-1+m)2+2k+1-2,an+1=2(2k-1+m)+1,
取k=5,

∴m≥6,∴n=24+5+m≥27.
∴使Sn>12an+1成立的n的最小值为27.
【点评】合理分组是解决本题的关键.为什么分组呢?因为目标是求出Sn,而an的规律不易于找到,但{an}是由等差数列{An=2n-1}和等比数列{Bn=2n}组合而成,其和仍是基于等差数列{An}和等比数列{Bn}的和,而且{An}和{Bn}中无公共元素,也为解题减轻了负担.
对于这类插入或删除的题目的求和问题,合理分组求解是行之有效的,且是快捷的.
1.2 插入bn个常数
题目2已知an=3n,bn=3n,n∈N*,对于每一个k∈N*,在ak与ak+1之间插入bk个3,得到一个数列{cn}.设Tn是数列{cn}的前n项和,则所有满足Tm=3cm+1的正整数m的值为________.
【分析】数列{cn}是在数列{an}中插入bn个常数3构造而成.因此,按照ak分组,先各组内求和,再前k组求和,即可完成Tm的计算,进而解题.
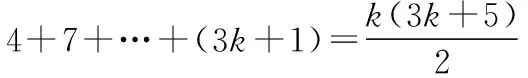
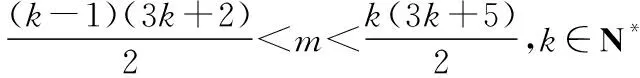


得5·3k-3k2-3k+1=0,
设f(k)=5·3k-3k2-3k+1,则f(k+1)-f(k)=10·3k-6(k+1)>0,∴f(k)是单调递增的,∴f(k)>f(1)>0.
∴此时Tm=3cm+1无解.
综上,满足Tm=3cm+1的正整数m的值为3.
【点评】分组将{cn}的规律显化,利于求和.
1.3 插入前k项
题目3已知等差数列{an}和等比数列{bn},其中{an}的公差不为0.设Sn是数列{an}的前n项和.若a1,a2,a5是数列{bn}的前3项,且S4=16.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅲ)构造数列a1,b1,a2,b1,b2,a3,b1,b2,b3, …,ak,b1,b2,…bk, …,若该数列前n项和Tn=1 821,求n的值.
【分析】(Ⅰ)(Ⅱ)略.(Ⅲ)由(Ⅰ)得an=2n-1,bn=3n-1,将{bn}的前k项插入ak与ak+1之间,构造新数列,将新数列按(ak,b1,b2,…bk)分组,先各组求和,再对前k组进行求和.
【解析】(Ⅰ)an=2n-1,bn=3n-1;(Ⅱ)t=0或2;

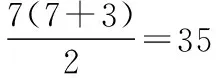


∴当Tn=1 821时,n=35+1+5=41.
【点评】分组是为计数和求和服务的.各组中{an},{bn}元素的个数,以及它们的和,都是考查的重点.
1.4 相间排列
题目4设等比数列{an}的首项为a1=2,公比为q(q为正整数),且满足3a3是8a1与a5的等差中项.数列{bn}的前n项和为Sn=n2,n∈N*.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若不等式λbn≤Sn+6对任意n∈N*都成立,求实数λ的取值范围;

【分析】(Ⅰ)(Ⅱ)略.(Ⅲ)由(Ⅰ)(Ⅱ)得an=2n,bn=2n-1,则cn是由an,bn中的某些项相间排列而成.分析各项特点,抓住奇偶解决问题.
【解析】(Ⅰ)an=2n;(Ⅱ)bn=2n-1,λ≤3;

故,当等差数列项数最大(最大为5)时,满足条件的等差数列为:1,2,3,4,5或5,4,3,2,1.
【点评】cn:1,2,3,4,5,8,7,16,9,…,按照定义写出这个数列,就能发现题目所求的目标.本题中,实际上有两种构造数列的方式:①命题人给出的构造方式——cn的构造是选取自an,bn;②解题者构造方式——在cn中选取,要求组成等差数列.
1.5 自身的嵌入


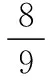
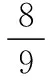
分组是为了更好地寻找构造数列的规律.找到了构造数列的规律,题目就迎刃而解.
题目6(2017·全国卷Ⅰ理·12)几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推,求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是( )
A.440 B.330
C.220 D.110
【分析】寻找一个数N,使得N>100且该数列的前N项和为2的整数幂,本质上仍是求数列的前n项和.而数列的构造方式是用等比数列的前k项重复组合而成,自然的想法是分组.



即2k-1=2+n(k∈N*,n≥14),
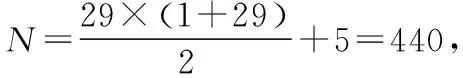
【点评】数列是密码设置的常用手段.寻找激活码的过程就是构造数列的过程.分组的作用仍是计数与求和.
二、数列中的“出”
数列中插入一些新元素,打破原有的规律,构造新秩序,形成新数列,是数列中的“入”.对应“入”,必然有“出”.将数列中的某些项舍去,也会打破原有的规律,从而缔造新秩序,但新秩序与原有的秩序是有关系的,也可能是解题的突破口.如何求解通过“出”构造的新数列的问题呢?分组也是一个好方法.
2.1 删除某些项
题目7记等比数列{an}的前n项和为Sn,已知a1+a3=30,3S1,2S2,S3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足b1=3,bn+1-3bn=3an,求数列{bn}的前n项和为Bn;

【分析】(Ⅰ)(Ⅱ)略;(Ⅲ)删除{an}中的第3项,第6项,第9项,…,第3n项,则原来的数列的项的位置发生了变化,而影响数列的通项公式.但仍可以通过原来的通项公式求解.


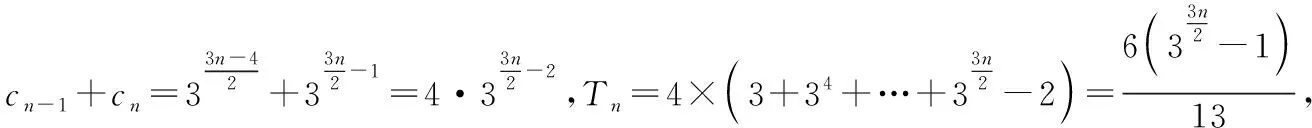
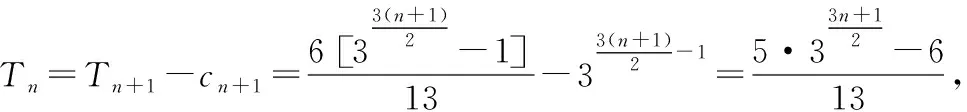


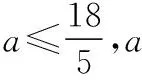
【点评】求{cn}的前n项时,应用了分组:将相邻两项并项,再求和.本质上,一个数列中删除某些项时,如果是按照等差数列的形式删除的,都可以用上述方法求解.
删除一些项保留另一些项,造成一种维纳斯之残缺的美,是数学中的奇异美.消除这个“异”的手段是分组求和,属于消除差异思想的应用.
2.2 挑出某些项
将数列中的某些项挑选出来,构成新的数列,也是命题的常用手段.最常见的是等差数列中的某些项成等比,或等比数列中的某些项成等差.
题目8设{an}是公差为d的等差数列, {bn}是公比为q(q≠1)的等比数列.记cn=an+bn.
(Ⅰ)求证:数列{cn+1-cn-d}为等比数列;
(Ⅱ)已知数列{cn}的前4项依次为4,10,19,34.
(ⅰ)求数列{an}和{bn}的通项公式;
(ⅱ)是否存在元素均为正整数的集合A={n1,n2,…,nk}(k≥4,k∈N*),使得数列cn1,cn2,…,cnk为等差数列?证明你的结论.
【分析】(Ⅰ) (Ⅱ)(ⅰ)略;(ⅱ)本质上是从{cn}中至少挑选出4项,组成等差数列.这样能否做到?分析cn的特点,抓住等差中项公式,构建方程,通过对方程的解的分析完成解答.
【解析】(Ⅰ)cn+1-cn-d=(q-1)bn;(Ⅱ)(ⅰ)an=3n-2,bn=3×2n-1;
(ⅱ)由题意得cn=3×2n-1+3n-2,则cn是单调递增的,且恒正.
假设存在满足题意的集合A,不妨设m,n,k,p∈A,m
若k>n+1,则k≥n+2,由2cn>ck有3×2n+6n-4>3×2k-1+3k-2≥3×2n+1+3(n+2)-2,即3(2n-n)+8<0,但n≥2时2n-n>0,两者矛盾,故k=n+1.
同理可得p=k+1,∴cn,ck,cp是数列{cn}中相邻的连续三项,∴2cn+1=cn+cn+2,
2(3×2n+3n+1)=3×2n-1+3n-2+3×2n+1+3n+4,即2n-1=0,此时无解.
故假设不成立,从而不存在满足题意的集合A.
【点评】本题中,cn是由两个正项的单调递增数列相加得到,再从中挑出4项成等差数列,既有数列的“入”,又有数列的“出”.将两种命题方式结合,加大了试题的难度.

