双变量不等式问题的解决策略
2018-12-06广东马少君
广东 马少君
近几年高考数学试题,如2018年全国卷Ⅰ理科数学21题,各地高三模拟数学试题中,涉及两个变量的不等式问题,将导数与函数、方程、不等式知识结合在一起作为最后一道压轴题.这类问题由于变量多,导致学生拿到试卷后无从下手,找不到解题的突破口.而解决这类问题的常用方法是合理地等价转化为相对熟悉的问题——构造函数,把双变量问题转化为一元问题,再以导数为工具就能有效解决.下面就此类问题的处理技巧和方法加以归纳总结,以此抛砖引玉.
类型1消元构造法(挖掘题目隐含条件,寻找双变量等式关系,消元化为一元函数)
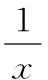
(Ⅰ)讨论f(x)的单调性;

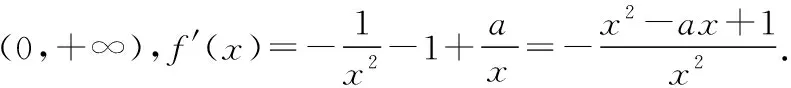
(ⅰ)若a≤2,则f′(x)≤0,当且仅当a=2,x=1时f′(x)=0,所以f(x)在(0,+∞)上单调递减.




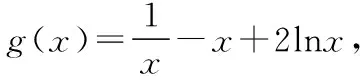



(Ⅰ)求a的取值范围;
(Ⅱ)设两个极值点分别为x1,x2,证明:x1·x2>e2.

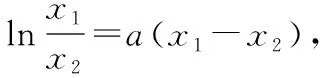
类型2 分离变量法
2.1两个变量地位均等,相互独立,若能分离,则分离后各自构造相应的一元函数.
例2已知函数f(x)=(a+1)lnx+ax2+1.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)设a<-1.如果对任意x1,x2∈(0,+∞),|f(x1)-f(x2)|≥4|x1-x2|,求a的取值范围.

(Ⅱ)不妨设x1≥x2,当a<-1时,

点评本题第(Ⅱ)问利用单调性去掉绝对值符号,分离两个变量,再构造函数利用导数处理.一般地,若两个变量分离到不等式两侧后,会化归为两种形式:(1)形如f(x1)>g(x2),则利用两侧函数各自的最值去处理;(2)形如f(x1)>f(x2),则利用函数的单调性来处理.



2.2两个变量无法分离,则合二为一,换元后构造一元函数.

(Ⅰ)若函数f(x)在定义域内不单调,求实数a的取值范围;
(Ⅱ)若函数f(x)在区间(0,1]内是增函数,求实数a的取值范围;
(Ⅲ)若x1,x2∈R+,且x1≤x2,求证:(lnx1-lnx2)(x1+2x2)≤3(x1-x2).


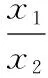
第一步:将两自变量变为一个整体,根据所得不等式构造合适函数.
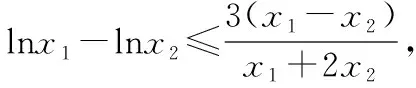
第二步:结合题中的函数和所构造的函数,选择合适的参数值,分析函数的单调性,利用导函数的单调性来进行证明.

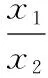
变式3已知函数f(x)=lnx.
(Ⅰ)求g(x)=(x2+1)f(x)-2x+2(x≥1)的最小值;




类型3指定主变量法(以一个变量为主变量,另一个变量为参数构造一元函数,或一个指定为变量,另一个看成常数,进而构造函数,巧妙转化为一元函数)
例4已知函数f(x)=ln(x+1)-x,g(x)=xlnx.
(Ⅰ)求函数f(x)的最大值;


当-1
又因为f(0)=0,所以当x=0时,f(x)取得最大值,且最大值为0.
(Ⅱ)g(x)=xlnx,g′(x)=lnx+1.



点评本题第(Ⅱ)问是函数背景下的双变量不等式的证明,在两个变量地位均等的条件下,以一个变量为主,另一个变量为参数巧妙地转化为一元函数,再移项构造函数,利用导数研究函数的单调性,求出最值加以证明.


点评本题借助“一动一静”的主元思想,巧妙地避开两个变量,直接构造函数,转化为函数模型解决问题.
类型4极值点偏移法
一、极值点偏移的含义




二、极值点偏移问题的一般题设形式
1.若函数f(x)存在两个零点x1,x2且x1≠x2,求证:x1+x2>2x0(x0为函数f(x)的极值点);
2.若函数f(x)中存在x1,x2且x1≠x2满足f(x1)=f(x2),求证:x1+x2>2x0(x0为函数f(x)的极值点);


三、运用判定定理判定极值点偏移的方法
1.方法概述
(1)求出函数f(x)的极值点x0;
(2)构造一元差函数F(x)=f(x0+x)-f(x0-x);
(3)确定函数F(x)的单调性;
(4)结合F(0)=0,判断F(x)的符号,从而确定f(x0+x),f(x0-x)的大小关系.
口诀:极值偏离对称轴,构造函数觅行踪;四个步骤环相扣,两次单调紧跟随.
2.抽化模型
答题模板:若已知函数f(x)满足f(x1)=f(x2),x0为函数f(x)的极值点,求证:x1+x2<2x0.
(1)讨论函数f(x)的单调性并求出f(x)的极值点x0;
假设此处f(x)在(-∞,x0)上单调递减,在(x0,+∞)上单调递增.
(2)构造F(x)=f(x0+x)-f(x0-x);
注:此处根据题意需要还可以构造成F(x)=f(x)-f(2x0-x)的形式.
(3)通过求导讨论F(x)的单调性,判断出F(x)在某段区间上的正负,并得出f(x0+x)与f(x0-x)的大小关系;
假设此处F(x)在(0,+∞)上单调递增,那么便可得出F(x)>F(x0)=f(x0)-f(x0)=0,从而得到x>x0时,f(x0+x)>f(x0-x).
(4)不妨设x1 接上述情况,由于x>x0时,f(x0+x)>f(x0-x)且x1 【说明】(1)此类试题由于思路固定,所以通常情况下求导比较复杂,计算时要引导学生细心观察; 例5已知函数f(x)=(x-2)ex+a(x-1)2有两个零点. (Ⅰ)求a的取值范围. (Ⅱ)设x1,x2是f(x)的两个零点,证明x1+x2<2. 解析:(Ⅰ)a的取值范围为(0,+∞). (Ⅱ)不妨设x1 又f(x1)=f(x2)=0,即证f(x2)>f(2-x2),即要证当1 令F(x)=f(x)-f(2-x)=(x-2)ex+a(x-1)2-[-xe2-x+a(1-x)2]=(x-2)ex+xe2-x,1 点评本题利用极值点偏移构造差函数F(x)=f(x)-f(2-x),然后对F(x)求导,利用单调性,不需要复杂的变形,切入点好,易操作.其解题的本质是x1与2-x2的大小关系不易直接比较时,通过化归转化为比较函数值f(x1) 与f(2-x2)的大小关系,再结合f(x)的单调性获得解决.


