重拾经典 领悟内涵 提升效能——一道数列题的解法规律及其应用

陕西 李 歆

一、从一道经典的高考题谈起

1.考题再现

【题目】 各项均为正数的等比数列{an}的前n项和为Sn，若Sn=2，S3n=14，则S4n等于

( )

A.16 B.26

C.30 D.80

这是2007年高考数学陕西卷理科第5题，是一道等比数列的选择题，该题看似简单，但得出结果却不易，通过该题的考查，能有效地检测考生对等比数列知识中所蕴涵的数学思想和方法的掌握程度.

2.遇到的困惑

看到这道题，由已知条件和待求问题，考生一般都会想到下列三个式子：

但对这三个式子的处理，一部分考生思路比较狭隘，容易把目光定位在③式中的a1，q和n的求解上，但是由①和②两个式子求不出这三个待求的量，感到条件不足，思维受阻.

3.“秒杀”解法

如果将目标聚焦到题目的四个选项上，那么就会发现问题的答案与n无关，由此“灵机一动”，可以取n=1试一试.

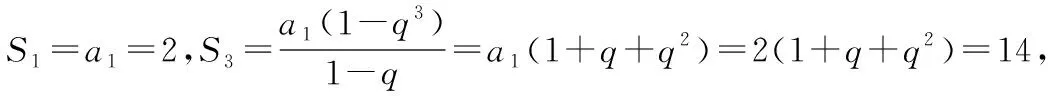
【点评】2005年江苏高考数学第3题：

在各项都为正数的等比数列{an}中，首项a1=3，前三项和为21，则a3+a4+a5=

( )

A.33 B.72

C.84 D.189

与上文中高考题取n=1的情况是同一类型题，因此，上文中的陕西高考题可以看成是江苏高考题的“改编”.

4.困惑的处置

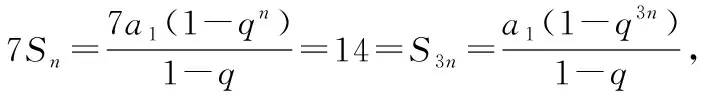
5.探寻规律

困惑解除后，学生往往会松一口气，进行别的问题.如果这样，就失去了经典考题的存在价值.事实上，在经典考题的“背后”，还隐藏着重要的智力资源，能给解题带来新的生机，教师要善于引导学生.

5.1寻找不同因式之间的关系

由④式易知，已知Sn和S3n的值，就可以求出qn的值，从而由⑤式就可以求出S4n的值.或者由⑤式易知，已知Sn和S4n的值，就可以求出qn的值，从而由④式就可以求出S3n的值.

5.2揭示未知与已知之间的通道

由于1-q4n=1-qn·q3n=(1-qn)+qn(1-q3n)，

1-q4n=1-q3n·qn=(1-q3n)+q3n(1-qn)，

因此，可得

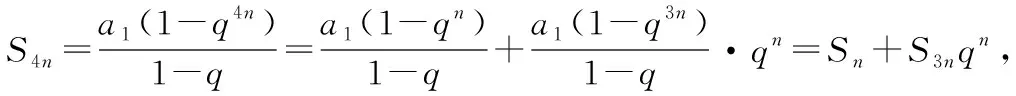
由⑥式和⑦式，易得Sn+S3nqn=S3n+Snq3n，由此，已知Sn和S3n的值，就可以求出qn的值，从而由⑥式或者⑦式就可以求出S4n的值.

【点评】有了④式和⑤式或者⑥式和⑦式，前面的困惑便烟消云散，考题也由难变易，这说明解题仅仅停留在解法1和解法2的层面是不够的，必须进一步探寻规律，抓住本质，这样才能把题解“熟练”、解“透彻”，由此解题能力方可得到历练与提升.

二、激活思想，领悟内涵，提升解题效能

通过对前面一道经典考题的求解以及内在规律的探究，我们隐约地预感到，在等比数列前n项和的公式中，存在着对解题具有一定价值作用的知识，需要我们再认识、再思考、再发现，从而在教学中传授学生.

1.改变等比数列的前n项和Sn的下标，探一探有什么发现？

在⑥式和⑦式中，不难看到Sn，S3n，S4n的下标之间存在着等量关系：n+3n=4n，由此可联想到一般情况下，是否也有这样的公式呢？经过探究，得到下面结果.

1.1性质

已知{an}为等比数列,Sn，Sm分别为前n项、前m项的和，若m>n，则有

Sm=Sn+Sm-nqn.⑧

【证明】(1)当q=1时，易知⑧式成立；

(2)当q≠1时，由等比数列前n项和公式，得

整理得⑧式成立，

综合(1)(2)可知，⑧式成立.

1.2一个推论

已知{an}为等比数列,Sn,Sm,Sk,St分别为前n项、前m项、前k项和前t项的和,若n-k=m-t>0,则有Sn-Sk=(Sm-St)qk-t.⑨

【点评】可以看到，公式⑧和公式⑨分别反映了等比数列前n项和Sn的下标在变化过程中，满足“和相等”与“差相等”关系时，所具有的等量关系式.这两个公式，在常规教学中是见不到的，它们是等比数列前n项和公式的深化，对解决等比数列前n项和的有关问题具有重要的指导作用.

2.应用举例，优化解题

在等比数列前n项和公式的应用教学中，教师如果只满足于让学生记住基本公式的结构特征，那么一般学生就会拘泥于按部就班的罗列求和公式解题，思维容易形成定式，但是，有了上面的性质与推论以及产生的过程与背景，那么学生的解题思路就能完全放开，从而既缩短了运算过程，又提高了解题效率.

2.1公式⑧的应用

2.1.1已知Sn，Sm，Sk中某两项的值，求另一项值的问题.

【例1】设等比数列{an}的前n项和为Sn，若S3=3,S6=9,则S9=________.

【变式1】各项均为正数的等比数列{an}的前n项和为Sn，若S3=2,S9=14，则S12等于

( )

A.16 B.26

C.30 D.80

【提示】由公式⑧可得S12=S3+S9q3=S9+S3q9，则得2+14q3=14+2q9，整理得q9-7q3+6=0，解得q3=2(q3=1即q=1不符，舍去)，所以S12=2+14×2=30.

【变式2】 设等比数列{an}的前n项和为Sn，若S2=2,S4=10,则S10=________.

【点评】此类题型，在求等比数列前n项和的问题中比较常见，如果k=n+m，那么就可以直接由公式⑧求解；如果k>n+m，那么可以先利用公式⑧求出Sn+m，然后看2n+m或者n+2m是否与k相等，如果相等，即可再一次利用公式⑧求解，直到得到结果.

2.1.2Sn和Sm的倍数或者商的关系与公比q的求值问题

【变式1】一个各项均为正数的等比数列，它的前4项之和为前2项之和的5倍，则此数列的公比为________.

【提示】由已知条件可知S4=5S2，则由公式⑧可得S4=S2+S2q2=5S2,解得q=2.

( )

A.2 B.4

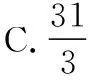
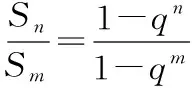
2.2公式⑨的应用

( )

A.2 B.3

C.4 D.5

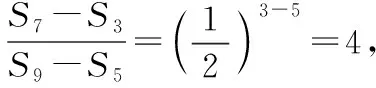
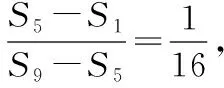
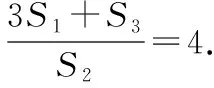
2.2.2分子与分母都是若干项的和的分式的求值问题

( )

________.

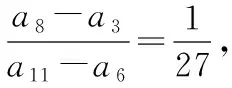
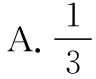
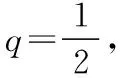
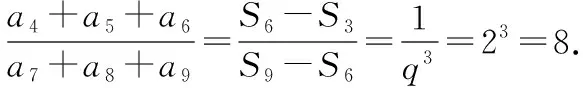
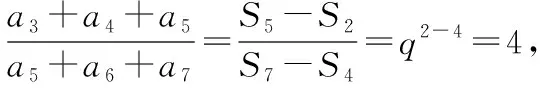
【点评】此类题型，用一般方法去解，思路比较僵化，过程也很复杂，但用⑨式，却思路清晰，过程简捷，既能提高解题速度，又能避免复杂运算中可能出现的错误.

三、思考与感悟

常言道：刷百题不如解透一题.前者“刷百题”追求的是解题的“量”，后者“解透一题”讲究的是解题的“质”，显然，“质”比“量”更为重要.教学实践证明，题不是刷得越多越好，如果缺乏解题反思，不但浪费时间，甚至会误导学习.因为反思的过程是对基础知识和解题方法理解与强化的过程，也是知识内化为能力的过程.所以，解题的本质，不在于运用了哪些知识，而在于是否触发了思考，激活了思维拓展.