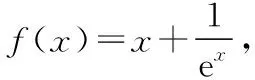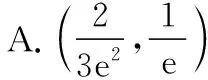经典真题与多解多变的完美结合

安徽 张 威

我们知道教师讲解典型例题是为了使学生对所学的知识融会贯通，开阔思维，培养其发散思维和创新思维能力，从而提高学习数学的兴趣，使得课堂更加高效.那么采用何种教学方法和形式才能达到这种高效呢？笔者认为对一些题型中的经典例题的讲解采用一题多解和一题多变的形式能更好地取得这种效果.比如在高考的客观题中，有一类题型是“含参不等式任意(存在)性问题”.这类问题是高考的热点和难点，也是重点.而很多学生看到这类问题往往是“望而生畏”，甚至是刚刚做过的题目，再遇到同类型或者有一些改变的题目，又不得而解.很大的原因还是思维不够开阔，对所学的知识不能融会贯通.下面笔者通过一道例题和变式题组来感受一题多解和一题多变的魅力.

【例1】(2008·江苏卷·14)设函数f(x)=ax3-3x+1(x∈R)，若对于任意x∈[-1,1],都有f(x)≥0成立，则实数a=________.

【例题分析】此题主要考查了含参不等式任意性问题，题型常规，题干简洁大气，含义深远.意在考查数形结合思想、分类讨论思想，运算求解能力、数据处理能力等.教师在讲解此题时，要引导学生回味此类题型的求解方法，让其进行对比、联想，从而得到求解的思路.而这一类问题主要涉及函数最值，常与导数工具相结合，并且与数形结合、分类讨论、转化与化归等数学思想紧密联系.解答此类问题，一般的思考角度为：①直接构造函数求最值；②分离参数构造函数求最值；③分离函数，利用数形结合思想求解；④特殊值代入求解.让学生通过上述思考角度，独立或与其他同学交流进一步完善解法.具体如下.

解法1：特殊值秒解法

因为此题是求解参数的具体值，故可以通过特殊值代入法进行求解，

【评注】此法具有一定的局限性，此题是求解具体参数值，故可以使用此法，如若求解参数范围，用此法就危险了.但是在导数压轴题中，采用此法，往往可以先缩小参数的范围，从而减少对参数的讨论，此法在解法3中展现得淋漓尽致.同时通过此法可以让一些基础薄弱的学生更加有信心，从而提升学习数学的兴趣.

解法2：直接构造函数，分类讨论求最值

由∀x∈[-1,1]，都有f(x)≥0成立，等价于f(x)min≥0，从而转化为求函数f(x)=ax3-3x+1在x∈[-1,1]的最小值.

接下来按照求函数最值方法求解即可，求导得f′(x)=3ax2-3=3(ax2-1).

①当a≤0时，显然可得f′(x)=3(ax2-1)<0，所以f(x)在x∈[-1,1]上单调递减，

此时f(x)min=f(1)=a-2≥0，得到a≥2，此时不满足条件；

但此时x∈[-1,1]，无法判断函数f(x)在x∈[-1,1]上的单调性，故需要进一步讨论.

则f(x)在x∈[-1,1]上单调递减，

所以f(x)min=f(1)=a-2≥0，得到a≥2，此时也不满足条件；

综上,a=4.

解法3：由解法1的思想，可以对解法2进行简化如下：

由已知，可得不等式f(1)≥0,f(-1)≥0恒成立，从而求解出一定有a∈[2,4]，

接下来只要判断a∈[2,4]中哪些值满足f(x)≥0恒成立，判断如下：

f′(x)=3ax2-3=3(ax2-1)，a∈[2,4]，

综上，a=4.

【评注】解法2、解法3主要是对参数进行分类讨论，而解法2处理以填空题出现的恒成立问题，稍显麻烦，得不偿失，但是作为解答题，用此法就是一个不错的方法.对于解法3是综合了解法1,2的思想进行了简化，与解法1和2比较可以发现，此法既严谨，又简单，无论是对选填和解答题都是一个不错的解法.同时在高考中为了为解答题赢得更多的时间，小题尽量节省时间，能用特殊法的要用特殊法求解.

解法4：分离参数构造函数求最值

由∀x∈[-1,1]，都有f(x)≥0成立，可对不等式ax3-3x+1≥0分离参数，即观察发现需要两边同除以x3，但是由于x∈[-1,1]，x3符号可能大于0，可能等于0，也可能小于0，故也需要分三种情况进行讨论，此时是按x进行分类：

所以g(x)在[-1,0)上单调递增，则g(x)min=g(-1)=4，

则a≤4；

②当x=0时，不等式ax3-3x+1≥0⟺1≥0，即此时a∈R;

则a≥4；综上，a=4.

【评注】分离参数对变量进行讨论一直是解决含参不等式的重要手段，即使不等式一端是含有参数的不等式，另一端是一个区间上具体的函数，有的题目通过分参会起到事半功倍的效果，所以此法学生要掌握.

解法5：分离函数，利用数形结合快速求解

(“分离函数”即是将不等式分离成两个函数，其中一个是含参的简单函数)

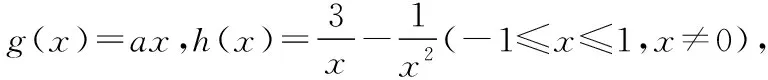
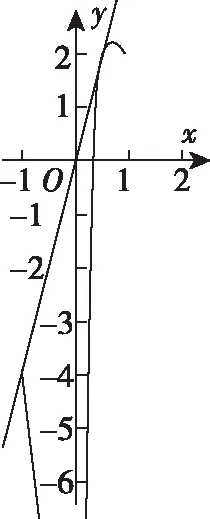
可知要先求出过(0,0)点该函数切线的斜率，设切点P(x0,y0),

此时直线恰好也过h(x)上的(-1,-4)这个点，可知对此切线的图象绕原点逆时针或顺时针旋转都不满足条件，故a=4.

②当x=0时，a∈R;

综上,a=4.

解法6：分离函数，利用数形结合快速求解

由ax3-3x+1≥0得ax3≥3x-1≥0(-1≤x≤1)，

令g(x)=ax3,h(x)=3x-1(-1≤x≤1)，即g(x)在-1≤x≤1区间上的图象恒在h(x)的图象上方；

由y=x3与y=3x-1的图象可知a>0，

大致图象如图所示：

可知要先求出满足条件的a使得y=3x-1为g(x)=ax3的切线，设切点P(x0,y0)，

当a逐渐变大时，(-1,-4)这个点在y=3x-1下方，此时不满足条件；

故a=4.

【评注】解法5、解法6求解思想一样，只是分离的函数不一样.是将函数中含参问题，分离成两个特殊的函数(最好将其中的一个函数分离成含参的直线)，再利用数形结合思想进行求解.此法对学生识图、作图、用图能力要求稍高，对一些分参和直接构造函数很难求解的问题，采用此法往往就是秒解法.

以上几种解法，是在师生共同探讨中得到的几个思考角度衍生出来的解法，可能有的学生会问：“这个例题的几个思考角度只适用于解答这类题目吗？”“这个题好旧啊！那么现在的高考还会再考吗？”无独有偶，在2018年高考中也可以用到，具体如下.

( )

A.[-1,0) B.[0,+∞)

C.[-1,+∞) D.[1,+∞)

【分析】此题主要考查了含参数的函数零点问题，题型依然很常规.可以发现此题是在【例1】的基础上，对函数的背景和设问角度进行变式，其思考角度与上述例题如出一辙.

解法1：直接构造函数，利用零点存在性定理求解

当x≤0时，g(x)=ex+x+a，则g′(x)=ex+1>0，

所以g(x)在(-∞,0]上单调递增，此时g(x)至多1个零点，

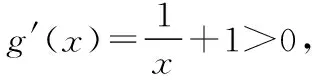
所以g(x)在(0,+∞)上单调递增，此时g(x)至多1个零点，

若g(x)存在两个零点，则g(x)在(-∞,0]和(0,+∞)上各有1个零点，

所以当x≤0时，g(x)max=g(0)=1+a≥0，即a≥-1，

①当a=-1时，显然g(0)=0，当x>0时，g(x)=lnx+x-1，显然g(1)=0，

所以g(x)有2个零点；

②当a>-1时，当x≤0时，g(0)>0，又因为ex+x+a<1+x+a，令1+x+a<0，

则x<-(a+1)<0，所以g(-a-1)<0，

由零点存在定理和单调性可得g(x)在(-∞,0]上有1个零点，

当x>0时，g(x)=lnx+x+a，因为g(e-a)=lne-a+e-a+a=e-a>0，

又g(e-a-1)=lne-a-1+e-a-1+a=e-a-1-1,因为a>-1，所以-a-1<0，

所以e-a-1<1，即g(e-a-1)<0，且0

所以由零点存在定理和单调性可得g(x)在(0,+∞)上有1个零点，

综上所述,a≥-1，故选C.

解法2：分离参数，利用数形结合思想求解

因为g(x)存在两个零点，所以方程f(x)+x=-a有两个不等实根，

即函数y=f(x)+x与直线y=-a的图象有2个交点，

y=lnx+x在(0,+∞)上单调递增，且y=lnx+x∈R，如图可得，-a≤1，故选C.

解法3：特殊值代入法

画出函数f(x)图象如图所示，

若g(x)存在两个零点，则y=f(x)与y=-x-a图象有两个交点，

当a=0时，显然y=-x与y=f(x)图象有2个交点，故排除A,D；

当a=-1时，显然y=-x+1与y=f(x)图象有2个交点，故排除B,

故选C.

解法4：分离函数，利用数形结合思想求解

因为g(x)存在两个零点，所以方程f(x)=-x-a有两个不等实根，

即函数y=f(x)的图象与直线y=-x-a有两个交点，

因为y=-x-a的图象是由直线y=-x的图象进行上下平移得到，

故对直线y=-x进行上下平移，如图所示.

故可得-a≤1，即a≥-1，故选C.

通过上述变式题，可以发现一题多变是运用不同的知识和方法，对有关数学概念、定理、通性通法等进行不同角度、不同层次、不同背景的变化，有意识地引导学生从“变”的现象中发现“不变”的本质，从“不变”中探求规律，从而达到对知识、方法等熟练掌握和灵活运用.下面几个变式也是从题干、设问角度、背景等对上述例题的变式.

( )

A.(-∞,1-e) B.(1-e,1]

C.[1,e-1) D.(e-1,+∞)

【答案】B.

【变式3】函数f(x)=ax3+(a-1)x2-x+2(0≤x≤1)在x=1处取得最小值，则实数a的取值范围是

( )

【答案】C.

【变式4】若关于x的不等式xex-ax+a<0的解集为 (m,n) (n<0)，且(m,n)中只有一个整数，则实数a的取值范围是

( )

【答案】D.

通过上述的变式题组，可以知道一题多变最终是为了通过变化让学生掌握变化中的不变，能从不同方面、不同角度和不同情况来说明某一事物，从而概括出事物的一般属性.因此，适当的变式能够使学生确切地掌握数学知识.另外，数学题目是永远做不完的，如果善于变式，在变式中掌握一类问题的解法，则会以少胜多，从而使得课堂教学更高效.