回归教材的新视角

福建 宋建辉

高考命题高度关注教材在命题中的作用，充分发挥教材作为试题根本来源的功能，而在高考考场上，我们的考生到底靠的是什么？靠的是对教材的熟悉，对教材中知识的理解，对教材中数学思想的领会，对教材中数学方法的掌握，因此高考复习应该，也必须回归教材.以下从4个视角谈谈如何回归教材，共同探讨回归教材的做法.

视角1：源于教材的定理公式

源于教材的定理或公式证明曾在高考中多次出现，如2010年四川卷第19题证明两角和的余弦公式与正弦公式；2011年陕西卷第18题叙述并证明余弦定理；2012年陕西卷理科第18题三垂线定理及逆定理的证明与表达；2013年陕西卷理科第17题推导等比数列的前n项和公式；2013年陕西卷文科第17题推导等差数列的前n项和公式等.

源于教材的定理或公式证明是数学知识最重要的内容，其中证明的方法所蕴含的数学思想方法是学生解决众多数学问题可以借鉴的，这应引起教师的重视.

案例1：已知点P(x0,y0)，直线l：Ax+By+C=0，且点P不在直线l上.

简解：(1)略.

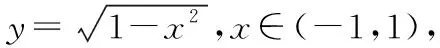
点评：点到直线的距离公式是解析几何中最重要的公式之一，它的推导证明蕴含了丰富的数学思想和方法.通过对公式推导证明的复习，不仅让学生“知其然”，还能“知其所以然”，更重要的是能进一步强化解析法对处理解析几何问题的重要性，培养学生运用等价转化、数形结合等数学思想方法解决问题的能力.而问题2，问题3的提出，对公式的理解、应用是一种提升，能充分激活学生的思维，提升数学核心素养，从而达到复习效果.

视角2：基于教材的整合改造

通过对历年高考试题的研究发现，高考试题的命制素材或直接源于教材，或间接源于教材，或由教材中的一道题微调而来，或由教材几道题串并组合而成，或由教材一道题引申拓展而得.因此我们在复习中要最大限度利用教材，发挥教材无法替代的优势，以教材中的例、习题为蓝本，进行类比加工，改编成思维含量较高又符合学生当前认知规律的题目，这样才能有效避免“题海战术”，减轻学生的复习负担，从而达到有效复习.

案例2：(人教A版必修2第144页复习参考题B组第2题阿波罗尼斯圆)

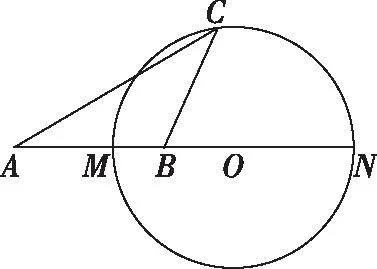
题组1.与面积有关的问题

简解：由阿氏圆定义知M的轨迹是一个圆，求出圆的轨迹方程，进而求得圆的半径，于是就会得到函数S=f(λ)，可判断其在(0,1)上单调递减，在(1，+∞)上单调递增.

题组2.与轨迹有关的问题

1.已知两定点A(-2,0),B(1,0),如果动点P满足条件|PA|=2|PB|,则点P的轨迹所包围的图形的面积等于( )

A.π B.4π C.8π D.9π

简解：易求得点P的轨迹方程为(x-2)2+y2=4,故选B.

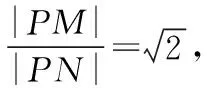
简解：以O1O2所在直线为x轴，以O1O2的中垂线为y轴，易求得点P的轨迹方程为(x-6)2+y2=33.

4.已知直角坐标平面上点Q(2,0)和圆C∶x2+y2=1，动点M到圆C的切线长与|MQ|的比等于常数λ(λ>0).求动点M的轨迹方程，说明它表示什么曲线.

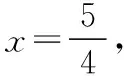
题组3.与阿氏圆有关的探索性问题

1.如图，圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方)，且|AB|=2.

(1)圆C的标准方程为________；

(2)过点A任作一条直线与圆O∶x2+y2=1相交于M,N两点，下列三个结论：

其中正确结论的序号是________.(写出所有正确结论的序号)

2.已知圆O∶x2+y2=1和点M(4,2).

(1)过点M向圆O引切线l，求直线l的方程；

(2)求以点M为圆心，且被直线y=2x-1截得的弦长为4的圆M的方程；

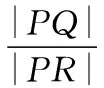
(2)圆M的方程为(x-4)2+(y-2)2=9.

又点P在圆(x-4)2+(y-2)2=9上，所以x2+y2=8x+4y-11，

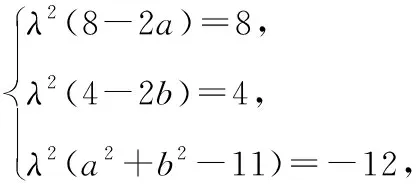
3.如图，圆C与y轴相切于点T(0,2)，与x轴正半轴交于两点M,N(点M在点N的左侧)，且|MN|=3.

(1)求圆C的方程；

(2)过点M任作一条直线与圆O：x2+y2=4相交于点A,B，连接AN,BN.求证：∠ANM=∠BNM.

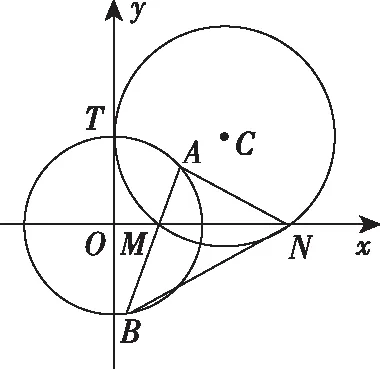
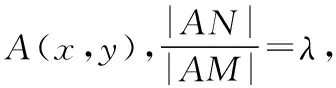
又点A在圆O：x2+y2=4上，

点评：以上题组均以阿氏圆为载体，题组涉及了解三角形、轨迹问题以及探究性问题，多角度、全方位复习了基础知识、基本技能、基本思想、基本活动经验，学生完全可以利用自己在平时学习中所掌握的方法来完成对试题的解读.整合策略的运用，避免了教材的局限，熟悉的文本又有利于唤醒学生对课堂教学过程的记忆，进而达成“得法于课内，得益于课外”的目的.

视角3：基于教材的延伸拓展

近年的高考试题，十分重视数学思想方法的考查，而教材中的例、习题一般都具有典型性、示范性和迁移性，它们或是渗透了某些数学方法，或体现了某些数学思想，或提供了某些重要结论，因此应充分认识例、习题本身所蕴含的价值，掌握其中的通性通法以及(二级)结论的应用.

案例3：圆锥曲线相关知识的专题复习方案

问题1：已知平面内动点与两定点A1(-a,0)，A2(a,0)(a>0)连线的斜率之积等于非零常数m的轨迹，加上A1,A2两点所成的曲线C可以是圆、椭圆或双曲线.请根据上述结论，探求曲线C的方程，并讨论曲线C的形状与m值的关系.

问题2：已知平面内动点与两定点A1(-a,0)，A2(a,0)(a>0)连线的斜率之和、差、商等于非零常数m的轨迹，探求动点的轨迹方程，并讨论动点的轨迹的形状与m值的关系.

题组训练：

解法一：利用椭圆的几何性质(二级结论)“椭圆短轴顶点对椭圆长轴的两个顶点的张角最大”，从这个角度出发，会得到优美简捷的解法.

A.sinαcosβ

C.sinα=cosβD.sinα与cosβ的大小不能确定

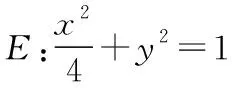
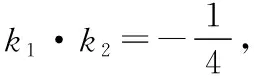
4.已知A，B为双曲线E的左、右顶点，点M在E上，△ABM为等腰三角形，且顶角为120°，则E的离心率为( )

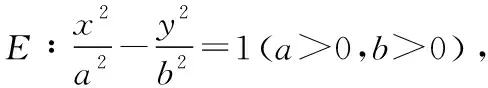
点评：该案例取材于人教A版教材，通过问题1及问题2，构建了一个圆锥曲线相关知识的微专题复习方案，而题组训练则强化了对知识的应用及理解，特别是“结论”的应用，对问题的解决起到了重要的作用.

因此在高考复习中，我们要注重对一些经典的、具有代表性知识的拓展延伸，尤其是教材中出现的，在弄清这些知识的发生、发展后，要及时加以整理归纳，形成结论，并通过一定的训练达到理解掌握，从而在具体问题的情景中灵活应用，助推问题的解决.

视角4：基于教材的数学文化

近几年高考加强了数学文化的考查要求，而教材中涉及数学文化的内容无疑是高考命题的最佳素材，这些试题的共同特点是：均取材于数学名著，都符合数学文化的要求，让考生直接感受到了数学文化的冲击，且这些试题难度不大.那么教师在复习中应对教材中出现的数学文化，特别是全国卷高考中未考查的内容予以关注并创造性地“教学”.

背景分析：该案例是基于人教A版必修2“探究与发现—祖暅原理与柱体、锥体、球体的体积”的内容而设计的，当然椭圆的面积公式是不要求掌握的，它的推导还可以有其他方法，例如利用定积分或随机模拟实验方法等，但这样的设计无疑是对数学文化的深层次的理解与应用.

引理：若夹在两条平行直线间的两个平面图形，被平行于两条平行直线的任一直线所截，如果截得的两条线段长的比例总相等，那么这两个平面图形的面积比等于截得线段长的比.(注：此定理相当于祖暅原理的推论，证明从略)

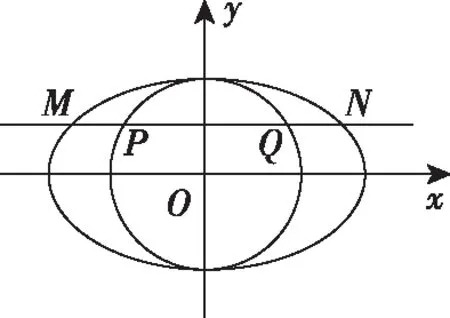
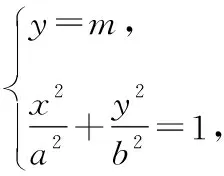
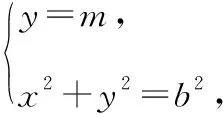
点评：此法适用于类似夹在两条平行直线间的平面图形，若被平行于两平行直线的任一条直线所截得的线段长成相等比例，当已知线段长的比值时，则可利用引理由一已知平面图形面积求另一平面图形面积，还可以提供以下解法，达到融会贯通，提升学生的核心素养的效果.

点评：将古代数学名著中的几道数学试题简单地拿来考学生，显然不代表数学文化.一道好的数学文化试题，一道有价值的数学文化试题，一定是将数学知识、思想、方法、文化融为一体，一定是蕴含了数学文化的“过程性”.数学文化为数学命题提供了更广阔的空间和载体，因此对数学文化的复习，应关注提炼数学文化中所蕴含的数学思想方法.