岩溶地区高速公路路桥基下伏溶洞顶板力学简化计算模型研究

陈 记，秦 溯，李云安，任娜娜，鲁贤成

(1.广东省南粤交通仁博高速公路管理中心，广东 韶关 512599;2.中国地质大学(武汉)工程学院，湖北 武汉 430074)

随着我国西部大开发及一带一路战略的实施与推进，线性工程的辐射范围越来越广，其不可避免地要穿越岩溶地貌。高速公路部分段穿越岩溶区时，不仅在建设阶段会面临地面塌陷或塌孔漏浆等高风险、高难度、高造价的问题，还会对日后运营构成极大的安全威胁[1]。岩溶地区高速公路路桥基下伏可溶岩中的溶洞顶板，很可能在自然与人为因素的影响下失稳而造成塌落或沉陷，严重威胁着其上路桥基等工程的安全稳定性[2]。因此，必须结合工程实际对岩溶地区高速公路路桥基下伏溶洞顶板的稳定性进行科学、合理的评价与判断，才能更准确地指导工程设计、施工及岩溶地质灾害的防治。

目前，国内外学者针对岩溶地区高速公路路桥基下伏溶洞顶板稳定性的评价方法主要分为3类：定性评价法、半定量评价法和定量评价法[3-9]。其中，定性评价法主要依赖人为主观上的判断，所得的评价结果具有一定的主观性；定量评价法虽能得到较为准确的评价结果，但其对溶洞发育基本特征、岩土体物理力学参数等信息的要求较高，而由于溶洞发育的隐伏性、岩土体各向异性等特点的存在，使该评价方法缺乏实际可操作性；半定量评价法作为一种定性与定量相结合的评价方法，主要通过建立溶洞顶板力学简化计算模型，运用力学原理及方法，以岩土体强度或变形量大小为判据对路桥基下伏溶洞顶板稳定性进行评价，因其评价结果具有科学、合理、便于应用的特点，故该评价方法在实际工程应用广泛，其中最为典型的方法是将溶洞顶板简化为梁板结构进行稳定性分析与评价[10-14]。但是，在根据路桥基下伏溶洞顶板实际受力情况对模型进行简化时，不同简化模型的计算结果往往相差较大，究其本质是因为所采用的溶洞顶板力学简化计算模型不能准确地描述或反映溶洞顶板强度或变形的特征，该模型是否适用还有待商榷。

本文在深入分析岩溶地区路桥基下伏溶洞顶板实际受力特点的基础上，建立了路桥基两种不同荷载作用下3类常用的梁结构模型，即简支梁模型、两端固定梁模型和悬臂梁模型；并基于材料力学理论引入奇异函数的初参数法，推导出6个简化模型的挠曲线方程；最后结合工程实例，运用数值模拟方法得到溶洞顶板位移云图，并将其与推导出的挠曲线方程计算结果进行对比分析，得到了溶洞顶板垂向位移分布特点及最适合的溶洞顶板力学简化计算模型，以期为岩溶地区高速公路路桥基的稳定性分析与评价提供依据。

1 溶洞顶板力学简化计算模型及其挠曲线方程

1. 1 路桥基下伏溶洞顶板力学简化计算模型

对岩溶地区高速公路路桥基工程的安全性评价，往往可归结为对路桥基下伏溶洞顶板稳定性的评价。通过钻探、物探等有效勘察手段确定溶洞发育特征后，根据工程实际情况建立科学、合理、便于应用的路桥基下伏溶洞顶板力学简化计算模型，成为对岩溶地区高速公路路桥基工程进行安全稳定性评价的关键。假设溶洞为顶板厚度均一的立方体，即可将顶板视为梁模型。根据溶洞顶板实际所受约束的特点，主要划分为3类梁结构模型：简支梁模型、两端固定梁模型和悬臂梁模型。又根据溶洞顶板顶面的受力特点，将路基下伏溶洞顶板所受力视为均布荷载，桥基下则视为一中部集中力，而两种荷载作用下3类梁结构模型可组合成6个路桥基下伏溶洞顶板力学简化计算模型，详见图1。

图1 路桥基下伏溶洞顶板力学简化模型Fig.1 Mechanical simplified models of karst cave roof under highway roadbed and bridge foundation注：q表示作用在梁上的均布荷载；F表示作用在梁上的集中力；l表示梁的全长；为了便于后续分析，将xy直角坐标系的原点o设置在梁的左端面形心处，x表示距原点o的梁横截面形心的位置，y表示x处梁截面形心向下的位移

1. 2 溶洞顶板力学简化计算模型的挠曲线方程

溶洞顶板在均布荷载或中部集中力的作用下，会产生一定的变形量，当变形量超过临界值后，顶板将失稳破坏，因此可将顶板变形量作为反映溶洞顶板在外部荷载作用下稳定性的判据或评价指标[15]。在材料力学的梁结构模型中，挠度y定义为梁横截面形心在垂直于轴线方向上的线位移，而挠曲线方程又是梁在横截面位置为x处的挠度y的函数。故可通过各溶洞顶板力学简化计算模型的挠曲线方程，求得溶洞顶板各位置处的挠度y，用来反映溶洞顶板的稳定状况。

对于梁结构挠曲线方程的推导，以往是先求得梁结构的弯矩方程，再通过梁结构挠曲线的近似微分方程并进行二次积分求解，在此过程中产生的积分常数通过边界条件或变形协调条件解得。这种方式虽能准确地推导出梁结构的挠曲线方程，但其过程较繁琐，且对于超静定结构梁的挠曲线方程推导较为困难。本研究引入奇异函数的初参数法，在这一方法中，不论荷载如何复杂，是否为超静定结构，梁结构的挠曲线方程都能用一个统一的方程表达，具有较好的普适性[16]。

1.2.1 奇异函数

设一函数簇fn(x)，其定义为

(1)

为区别于一般函数，上式中使用了尖括号，这种形式的函数称为奇异函数。奇异函数的积分法和求导法则为

(2)

(3)

1.2.2 梁结构挠曲线的初参数方程

梁结构挠曲线的初参数方程的推导以简支梁模型为例，见图2。

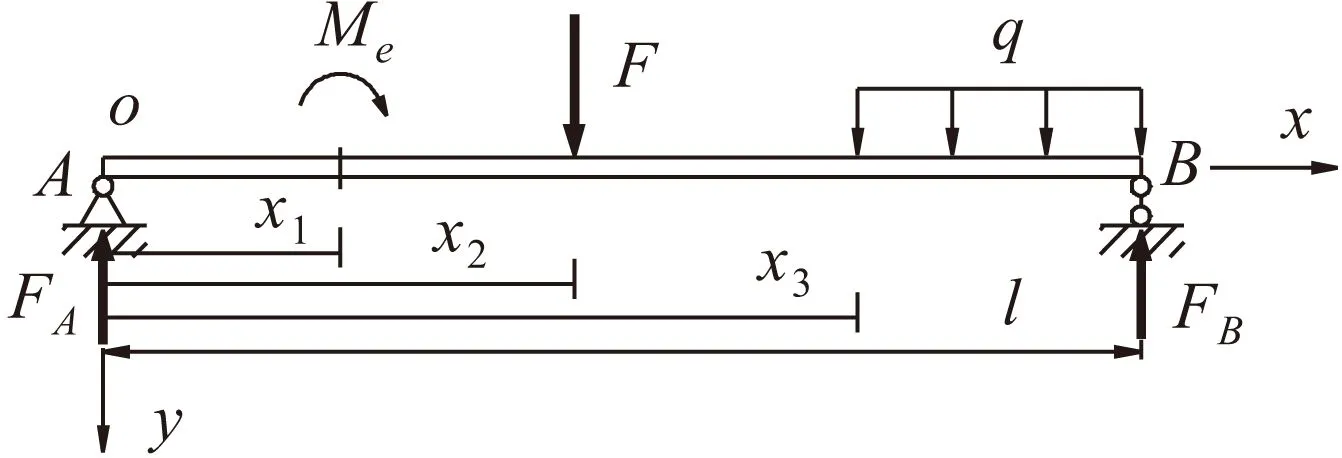
图2 简支梁结构挠曲线方程推导的一般模型Fig.2 Universal model for deriving the deflection curve equation of simply supported beam structure注：作用在梁上的力有集中力F、集中力偶Me、均布荷载q以及作用在梁左右两端(A、B)的支座反力FA和FB;l表示梁的全长；xy直角坐标系的原点o设置在梁的左端面形心处;x1、x2分别表示梁上集中力偶Me和集中力F相对于坐标原点o的位置;x3表示开始出现均布荷载q时相对于坐标原点o的位置

利用奇异函数结合梁结构挠曲线的近似微分方程，经二次积分后，得到梁结构挠曲线的初参数方程如下：

(4)

(5)

式中:EI为梁的弯曲刚度;FS0、M0、θ0和y0分别为初始截面(x=0)上的剪力、弯矩、转角和挠度，统称为初参数，对于静定结构梁，只需通过力与力矩的平衡及边界条件确定，而对于超静定结构梁，则还需要通过确定基本静定系及变形几何相容方程并进行综合分析来确定初参数[17]。

对于所建立的6个溶洞顶板力学简化计算模型，利用上述原理及公式(4)、(5)进行求解，最后化简得到各简化计算模型对应的初参数值和挠曲线方程，详见表1。

2 工程实例应用与分析

2. 1 工程概况

由于区域内可溶性碳酸盐岩的存在以及具有溶蚀性和循环交替性的地下水，导致该区域岩溶强烈发育，主要为埋藏型溶洞，经统计区域内钻孔岩溶能见率为38.0%，钻孔平均线岩溶率为55.6%，钻孔最大线岩溶率87.5%，其中充填型溶洞(全充填和半充填)居多，钻孔揭露的溶洞发育情况见图4。

表1 溶洞顶板力学简化计算模型对应的初参数值和挠曲线方程

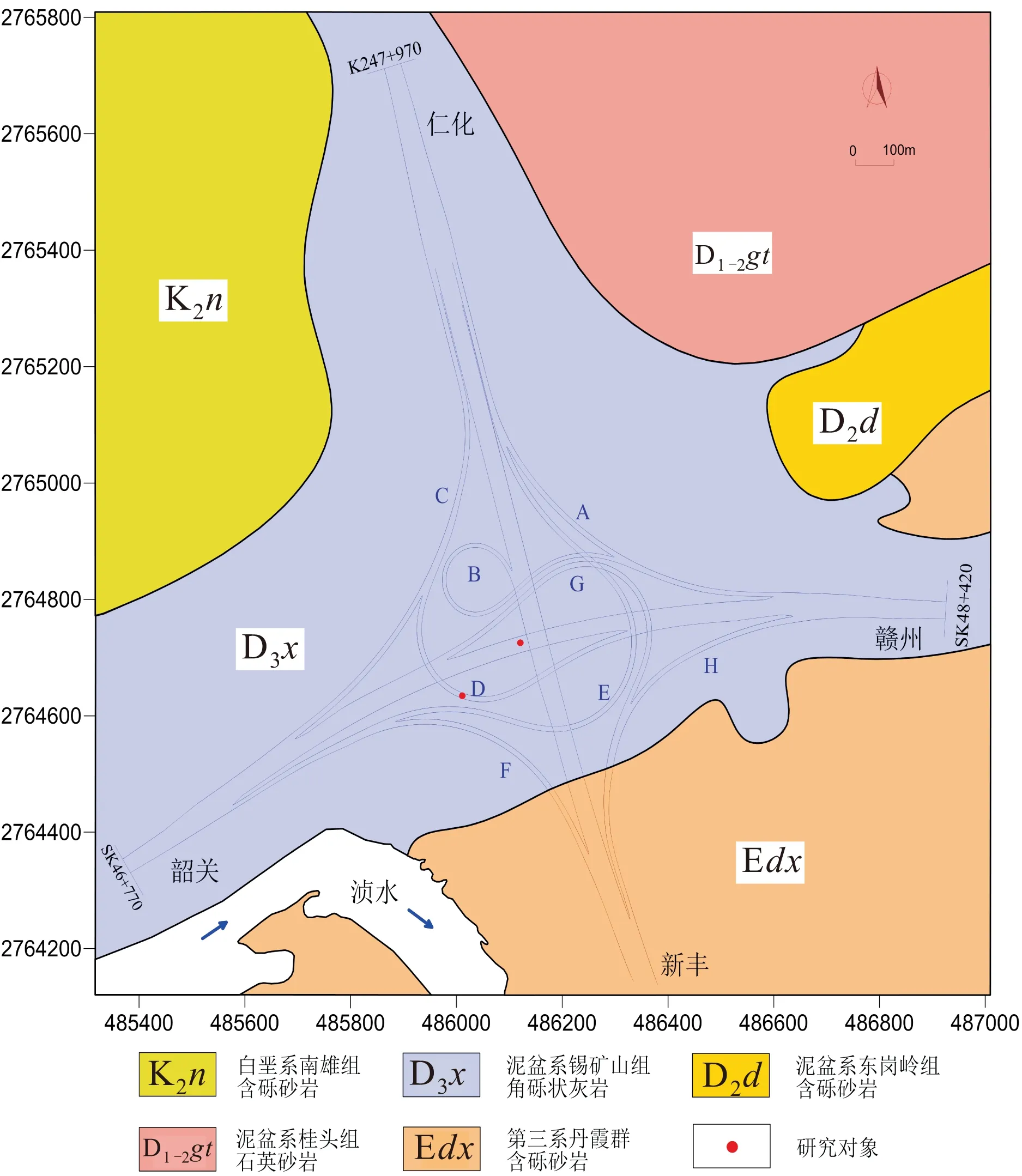
图3 丹霞枢纽高速公路互通区工程地质平面图Fig.3 Engineering geological map of Danxia grade separation area

图4 钻孔揭露的溶洞发育情况Fig.4 Boreholes revealing the development situation of karst cave

由于区域内岩溶强烈发育，目前已造成了韶赣高速路面脱空、局部沉降，路基边坡失稳，挡土墙断错等严重威胁线路安全运营的工程地质问题，故必须结合工程实际，建立科学、合理、便于应用的溶洞顶板力学简化计算模型，为区域内的岩溶稳定性评价奠定基础。

为了便于研究，本文选取韶赣高速公路基下伏一溶洞和D匝道桥(桩)基下伏一溶洞作为研究对象。其中，路基下溶洞跨度为11.2 m，顶板厚度为1.4 m，顶板顶面作用均布荷载为630 kN/m2；桥基下溶洞跨度为20 m，顶板厚度为3.3 m，顶板顶面中部作用集中力为5 400 kN。两溶洞顶板岩性相同，均为中风化角砾状灰岩，其物理力学参数：容重为27 kN/m3，弹性模量为35 GPa，泊松比为0.3，单轴抗压强度为40 MPa，单轴抗拉强度为4 MPa。

2. 2 路桥基下伏溶洞顶板挠度计算与对比分析

基于前面建立的溶洞顶板力学简化计算模型，将上述溶洞顶板及荷载参数代入推导的6个挠曲线方程中，分别计算出各个简化计算模型对应的挠度并绘制挠度分布曲线。实际中，对于埋藏型溶洞顶板的位移情况是很难监测的，而数值模拟则是一种能较为真实地反映应力场和位移场的方法。为了验证溶洞顶板力学简化计算模型的合理性，本文基于前述溶洞顶板及荷载等参数，采用有限元数值模拟方法构建路桥基下伏溶洞顶板受力模型，模拟得到路基下伏溶洞顶板在均布荷载和中部集中力作用下y方向的位移云图，见图5和图6。

由图5和图6可见，溶洞顶板无论是在均布荷载还是在中部集中力作用下，其挠度分布均是关于顶板中部对称的，且呈中间最大、两边最小的趋势。

将通过简化计算模型的挠曲线方程计算得到的顶板挠度与有限元数值模拟得到的顶板中线y方向位移，整理成表2和表3，并绘制路基下伏溶洞顶板均布荷载和桥基下伏溶洞顶板中部集中力两种荷载作用下挠度的分布曲线，见图7和图8。

图5 路基下伏溶洞顶板均布荷载作用下y方向位移 云图(有限元数值模拟)Fig.5 Contour for y displacement of karst cave roof under highway roadbed with uniform load

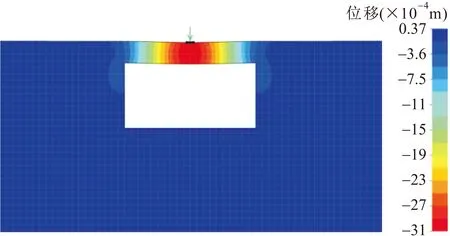
图6 桥基下伏溶洞顶板中部集中力作用下y方向位移 云图(有限元数值模拟)Fig.6 Contour for y displacement of karst cave roof under bridge foundation with central concentrated load

由表2和表3、图7和图8可以看出：

(1) 对于两种荷载作用下的3类溶洞顶板力学简化计算模型，其中简支梁模型和两端固定梁模型的溶洞顶板挠度y分布曲线是关于顶板中部呈开口朝上的抛物线对称分布，挠度y随x的增加由初始值0(顶板最左端)逐渐增大，在顶板中部挠度y达到最大值，然后又逐渐降至0(顶板最右端)，而悬臂梁模型的溶洞顶板挠度y分布曲线则是随x的增加由初始值0(顶板最左端)呈开口朝下的半抛物线状保持单调递增，在顶板最右端挠度y达到最大值。

表2 路基下伏溶洞顶板均布荷载作用下挠度计算结果对比

表3 桥基下伏溶洞顶板中部集中力作用下挠度计算结果对比

图7 路基下伏溶洞顶板均匀荷载作用下挠度的 分布曲线Fig.7 Deflection distribution of the karst cave roof under highway roadbed with uniform load

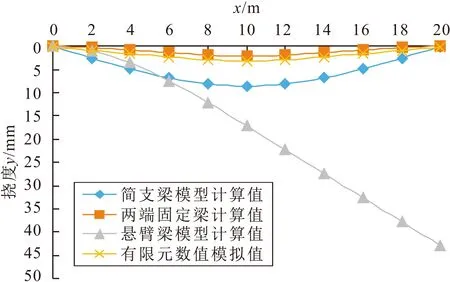
图8 桥基下伏溶洞顶板中部集中力作用下挠度的 分布曲线Fig.8 Deflection distribution of the karst cave roof under bridge foundation with central concentrated load

(2) 两种荷载作用下采用有限元数值模拟得到的溶洞顶板挠度分布曲线呈开口朝上的抛物线分布，在顶板中部挠度达最大值。

(3) 将6个溶洞顶板力学简化计算模型计算所得的计算结果与对应的有限元数值模拟结果进行了对比分析，结果发现3类简化计算模型中，简支梁模型和两端固定梁模型的溶洞顶板挠度分布曲线与有限元数值模拟的挠度分布曲线相似，挠度分布曲线均是关于顶板中部呈开口向上的抛物线型，且挠度中部最大，两端最小，说明以简支梁模型和两端固定梁模型作为溶洞顶部力学简化计算模型比悬臂梁模型更为科学、合理；而简支梁模型和两端固定梁模型中，两端固定梁模型的溶洞顶板挠度分布曲线与有限元数值模拟对应的挠度分布曲线最为接近，两者的挠度分布曲线相差不大几乎重合，说明两端固定梁模型相比简支梁模型能更准确地反映溶洞顶板的位移情况，故两端固定梁模型最适合作为路桥基下伏溶洞顶板力学简化计算模型。值得注意的是，采用有限元数值模拟所得的计算结果中，溶洞顶板两端挠度不为0，这是符合实际情况的，因为在实际中溶洞顶板在荷载作用下两端剪应力可能超过岩体的抗剪强度而发生破坏。

3 结 论

本文根据溶洞地区高速公路路桥基下伏溶洞顶板的实际受力特点，构建了两种荷载作用下3类溶洞顶板力学简化计算模型，并基于材料力学理论引入奇异函数的初参数法，推导出了6个溶洞顶板力学简化计算模型对应的挠曲线方程。选取广东韶关丹霞高速公路互通区路桥基下伏溶洞为研究对象，利用其几何特征及物理力学参数代入6个简化计算模型对应的挠曲线方程中，得到对应简化模型的挠度及其分布曲线。同时，采用有限元数值模拟方法建立了数值分析模型，模拟得出溶洞顶板竖向位移云图。通过将简化计算模型的计算结果与有限元数值模拟的结果进行对比分析，结果发现两种荷载作用下，简支梁模型和两端固定梁模型所得的计算结果与对应的有限元数值模拟结果基本相似，挠度分布曲线均为以顶板中部呈对称分布的开口朝上的抛物线型，且挠度中部最大、两端最小；悬臂梁模型的挠度分布则由左侧固定端保持单调递增；两端固定梁模型的挠度分布曲线与有限元数值模拟结果最为接近(两者几乎重合)，实际工程中宜采用两端固定梁模型作为路桥基下伏溶洞顶板稳定性评价的基础。