例析多元函数最值问题的求解策略

河南大学数学与统计学院 (475001)

卢 阳

一、不等式法

在最值问题中常用均值不等式、柯西不等式、绝对值不等式.运用不等式求最值时最大的难点在于如何“拆”、“拼”、“凑”，常见的有凑项数和凑系数，进而找到定值.

1.均值不等式

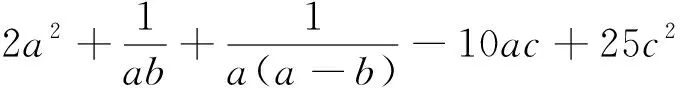
分析：此题无法直接运用不等式，观察到a2-10ac+25c2=(a-5c)2并且发现a2-ab=a(a-b)，故需要“拼凑”出-ab来.

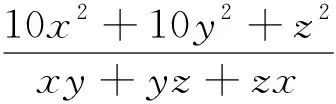
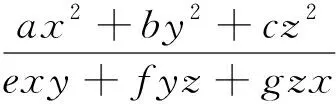
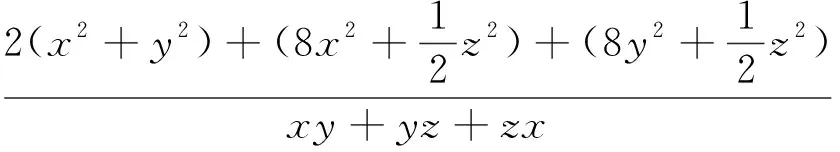
2.柯西不等式

例2 (2013年湖南卷理科第10题)设a,b,c∈R,a+2b+3c=6,求a2+4b2+9c2的最小值.

分析：注意到a2+4b2+9c2=a2+(2b)2+(3c)2，这是柯西不等式右边一组数的平方和.因此，需要配凑出另一组平方和.

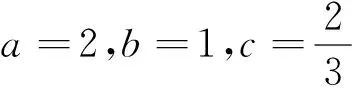
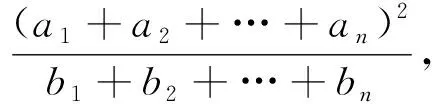
3.绝对值不等式

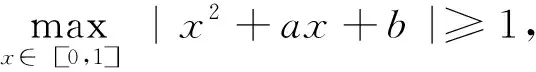
分析：该题若直接对绝对值中的二次函数进行讨论会比较繁琐，这里提供利用绝对值不等式的简便解法.

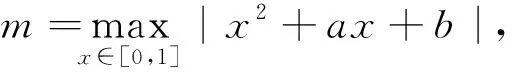
-3.

评注：运用不等式求多元函数最值时一定要先观察式子结构，选择恰当的不等式，再合理配凑找到定值，基本不等式找“积”、“和”为定值，柯西不等式找“方和积”、“积和方”为定值，绝对值不等式找“和”、“差”为定值，同时必须注意等号满足的条件.

二、消元法

若函数各元之间存在相依关系，可将各元用其中一个元来表示，便可化为常见的一元函数，再根据函数结构采用相应的最值求解方法.

例4 已知x,y，z∈R，且x+y+z=1,x2+y2+z2=3，求xyz的最大值.

分析：有关于x,y，z的两个等式，理论上可以找到x,y，z三者的关系，将三元函数变成一元函数.

变式(2017全国高中竞赛一试)已知实数x,y满足x2+2cosy=1，求x-cosy的范围.

评注：运用消元法求最值时需要根据题目条件和各元之间的关系求出最后所剩元的取值范围.

三、换元法

换元法是指通过引入一个或几个新的变量，来替换原来某些变量(代数式)，以便让问题得以解决的方法.常见的换元方法有代数换元、三角换元.

1.代数换元

分析：首先，观察式子结构，发现上式为齐次式，并且为对称式.式子的分子分母同除以x，便可以使用比值换元法.

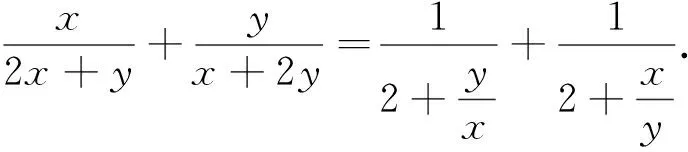
评注：在第一次换元后，也可用求导法求得最值.

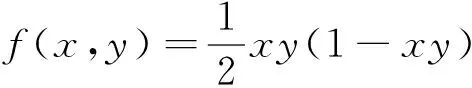
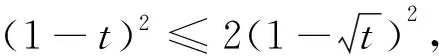
评注：比(倍)值换元在对称的齐次式中经常使用，但需注意对称式并非一定在各元相等时取最值，一定要耐心计算，切不可一心走捷径.特别提一下，近来年很火的极值点偏移问题，大都可以用比值代换的方式解决.

例6 (差值换元)已知实数x,y满足x2+y2+xy=1，求x+y的最大值.

分析：令x+y=t,代入x2+y2+xy=1，便可将y消去，变成x的一元二次方程.

2.三角换元

通过三角换元将多元函数变成三角函数，而三角函数的最值利用辅助角公式易求.掌握如下三角函数的恒等式是有必要的，如sin2α+cos2α=1，sec2α-tan2α=1，tanα+tanβ+tanγ=tanαtanβtanγ(α+β+γ=nπ(n∈Z)).

对于例6，还可以用三角换元解决.

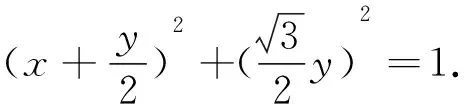
评注：在求解与圆锥曲线有关的最值问题时，利用三角换元往往可以降低难度.

变式(2018陕西预赛)设x,y∈R,且log4(x+2y)+log4(x-2y)=1,求x-|y|的最小值.

四、线性规划法

在求解最值问题时，如果条件与最值问题有对应的几何意义，便可利用数形结合思想，采用线性规划进行解决.

图1

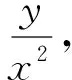
五、向量法

有些多元函数问题可以构造向量，将原来的问题变成向量问题，再利用向量的运算来简化问题.

对于例7的变式，已知x2+y2=4，求S=x+y+2最值还可以利用向量法将x+y看成两个向量的内积.

例8 已知a,b均为正数，且ab=a+b，求a+b的最小值.

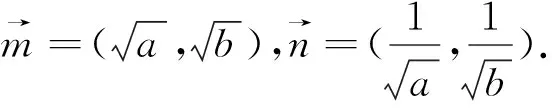
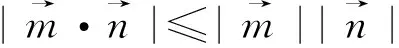
以上本着简洁、够用、减负的原则只介绍五种方法，但多元函数问题解法并非仅限于此.解决多元函数问题时不应局限于某一种做法，有时需多种方法交互，多样思维融合，这需要读者因题而异，仔细观察多元函数的结构和题目条件找到最优解法.