数形结合在高考解题中的应用

安徽淮北师范大学数学科学学院 (235000)

方 成 张 昆

数学是研究数量关系和空间形式的一门科学，简单的来说，就是研究“数”和“形”两大部分．数量关系中蕴藏着几何模型，几何中又涉及到数量关系．[1]其中，图形具备形象直观的优点，通常用于定性分析；而数量关系则需要依据数据进行分析．因此，在数学解题活动时，若能找到途径，将“数”和“形”两者形成有机结合，必能取长补短，会对探究问题的思路起到显著效果．对此，著名的数学家华罗庚先生曾说：“数与形，本是相倚依，焉能两边飞？数缺形时少直观，形少数时难入微，数形结合百般好，隔家分家万事休，切莫忘：几何代数统一体，永远联系，切莫分离．”[2]数形结合的思想已渗透到中学数学学习中，因此，在高考解题活动中，考生对某些特定问题的具体特点，选择以形助数或以数解形的途径是一条发现解决问题思路的比较好的手段．

一、求方程根的个数方面的应用

求解一般形式的方程的根的解法多样，例如配方法，求根公式等等．对于一些特殊形式的方程，考生们通常手足无措．这时候，可以转换另一种解题思路，将方程的根转化为函数的零点问题．而函数的零点是函数图像与x轴交点的横坐标，这涉及到图形方面的知识，而方程的根属于代数方面的内容．由此将代数与几何联系在一起．数形结合思想是将其联系在一起的一条支链．当选择一般途径解决不了代数问题时，可以借助“数形结合”转化思想，从“图形”方面考虑问题，进而寻求解决问题的途径．

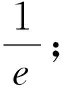
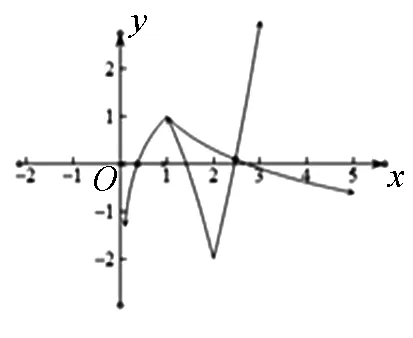
图1

解法2：由|f(x)+g(x)|=1，可得g(x)=-f(x)±1，分别作出函数的图像，分情况讨论：g(x)与h(x)=-f(x)+1的图像如图1所示，图像有两个交点；g(x)与φ(x)=-f(x)-1的图像如图2所示，图像有两个交点.所以满足方程

|f(x)+g(x)|=1的实根的个数为4．故答案为4．

图2

点评：比较这两种解法，可以看出运用方法二，从图像上直观看出有四个交点，方法简便．将方程的根与函数图形的交点联系一起，直观看出根的个数．而方法一分类过程较为复杂，且容易出错，学生在解题中遇到求函数单调性来判断函数是否与x轴存在交点问题，这一类问题容易造成学生思维障碍，求解过程受阻，不易解决．因此，绕过原来的思维障碍，直接从图形角度出发来解题．

二、求参数取值范围中的应用

参数，一般称为参变量或参变数，指相对于未知数来说可以在一定范围内取值的常数值或联系不同未知数之间的相关的未知数．求参数取值范围是高中数学中常见的一类问题，也是高考考查的重点之一．波利亚的思维方法表明：时刻不忘未知量．[3]所以在求参数取值范围的求解问题时，涉及的未知量很多，解题方式灵活多变．因此试着利用数形结合思想巧解这一类型的题目．

例2 (2014山东理8)已知函数f(x)=|x-2|+1,g(x)=kx．若方程f(x)=g(x)有两个不相等的实根，则实数k的取值范围是( )．

解析：由题意知，首先画出函数f(x)=|x-2|

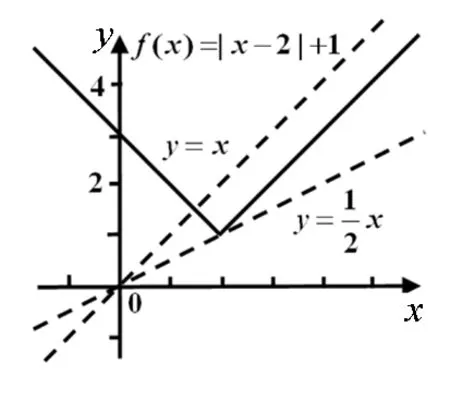
图3

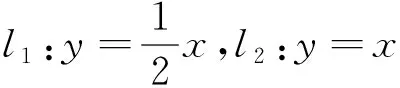
点评：求参数的取值范围的一般解法是分离参数，再求参数的取值范围．在此期间，不免加入了较为复杂的运算，所以求参数的取值范围的另一有效手段是借助图形，通过函数图像萌生出新的解法，而这种巧妙的解法比一般方法更加简洁．所以它在一定程度上有助于激发学生的创造性思维，并且起到事半功倍的效果．

三、求线性规划中的最值问题

线性规划问题是高考常见的考点之一．其中一类问题是求线性目标函数在线性约束条件下的最值问题，并把满足这个条件的解的集合称为可行域．线性规划中求最值问题借助图形能够直观的反映出来，“以形助数”，帮助考生解题．

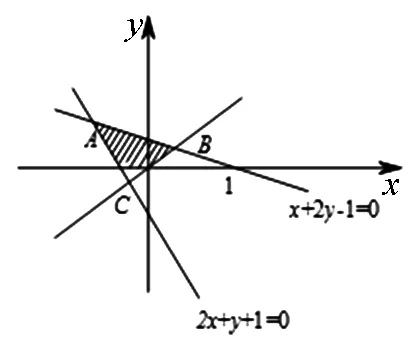
图4

分析：不等式组

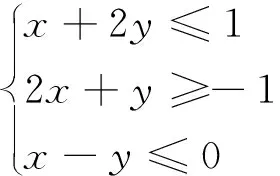
点评：本题的关键在于根据约束条件，准确做出可行域，利用数形结合找出最优解．

四、三角函数中的应用

研究三角函数的某些性质，往往借助图像法才能更好的解决对应的三角函数问题，借助图形转变能够直观的反映三角函数图形的性质，例如对称轴，平移后的函数图像，平移后的函数解析式等．

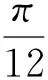
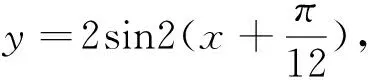
点评：数与形是数学的两大支柱，数形结合思想关键在于如何将数与形结合起来，通过图形研究三角函数的性质，直观分析，从而为发现解题思路创造条件．

五、几何概型中的应用

几何概型是指每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例，它属于概率论与统计学范畴．但其中也蕴含着数形结合的思想，下面以16年新课标高考数学的一道客观题为例．

图5

例5 (2016新课标理数2卷)从区间[0,1]随机抽取2n个数x1,x2,…,xn,y1,y2,…,yn构成n个数对(x1,y1),(x2,y2),…,(xn,yn)，其中两数的平方和小于1的数对共有m个，则用随机模拟的方法得到的圆周率π的近似值为( ).

点评：几何概型求概率是与构成该事件区域的长度(面积或体积)成比例，而面积和体积往往要借助图形，通过对图形进行观察，再利用代数方法求出概率．故数形结合思想应用其中．

六、解析几何中的应用

解析几何，将数与形紧密的结合在一起，笛卡尔曾经写道：古代人的几何和现代人的代数，都是研究非常抽象、毫无用处的题材，前者局限于考察图形，后者一味用规则和数字来约束，因此要找出另一种方法，包含它们的长处，没有短处．[4]故解析几何就很好的通过数量分析研究几何图形及其变化,是数与形的紧密结合．

图6

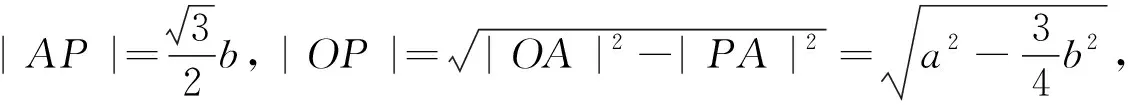
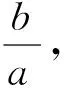
点评：该题巧妙的利用了数形结合的思想，以数解形，借助几何轨迹所遵循的数量关系，与几何定理相结合．找寻双曲线中各个系数之间的数量关系，再结合勾股定理，三角函数等求出双曲线的离心率．以形助数，以数解形，巧妙解题．

七、结语

问题解决，其实就是找到问题题设条件与所求结论之间的联结，而题设条件与所求结论之间存在着某种千丝万缕的联系．如何解题，就是要找出其中蕴含的某种关系．[3]数学的解题过程就像是抽丝剥茧一样，层层分析，步步为营，在变中找寻不变．而一旦解题过程中受阻，就要尝试转化思路，从另一个角度去分析问题，从而到达终点．在索解思路时，如果一味使用代数法或者几何法，很可能找不到解决问题的思路，或者陷入繁杂的计算中去．数形结合是比较好探索思路的方法．比如在求方程的根，函数的零点，不等式等等，如果用一般的方法不能解决时，就要转化思路，将它与图形联系起来，以形助数．同样的，如果解决某一图形时，试着找出图形之间的数量关系，用代数方法解决几何问题，又或是数形兼顾．因此数形结合在高考数学解题中具有独特的策略指导和调节作用．