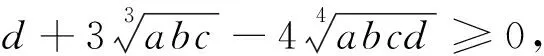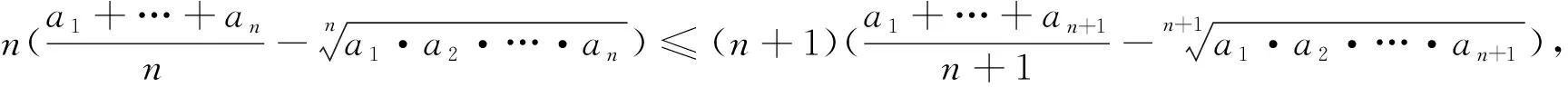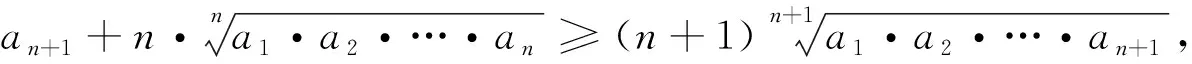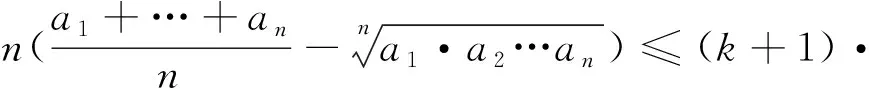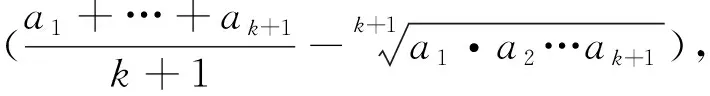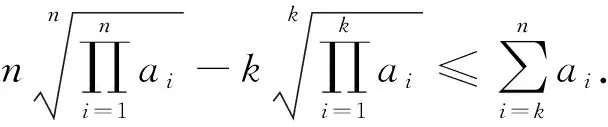一个不等式问题的思路分析与推广*

四川内江师范学院数学与信息科学学院 (641112)

纪定春 赵思林 杨 振

1.问题

2.思路分析

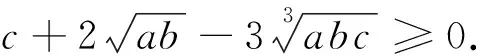
此处看到有根号，将根号“去掉”更加方便，可以考虑换元法．因为有开三次方和开平方两个根式，需要同时消除两个根号，则令a=x6，b=y6，c=z6，其中x，y，z>0．

那么，只需证：z6+2x3y3-3x2y2z2≥0(1)成立即可．

思路1分解因式法(直接法)

解析：(1)式的左边=z6+2x3y3-3x2y2z2=z2(z4-x2y2)+2x2y2(xy-z2)．

研究组术后出现脑积水1例，并发症发生率为3.33%（1/30）；参照组术后出现脑积水3例，颅内感染2例，切口疝2例，癫痫1例，并发症发生率为26.67%（8/30）。两组患者术后并发症发生率比较差异有统计学意义（P=0.026）。

令xy=m，z2=n，其中m，n>0，那么(1)的左边可化为n(n2-m2)+2m2(m-n)，将其进一步分解得(n-m)2(n+2m)≥0，当且仅当m=n，即ab=c2时取等，(1)显然成立．

评注：分解因式法是解决不等关系常见的一种操作手法．将一个多项式化为若干个次数较低多项式的乘积的形式，此处主要是巧用代换的方式减少了一个“元”，再与分解因式相结合，很易证明原命题成立，此方法难点在于对项数进行合理处理，此处可培养学生的数学直觉思维，提高数学核心素养．

思路2 “减元”法

法1:齐次式“降次”法

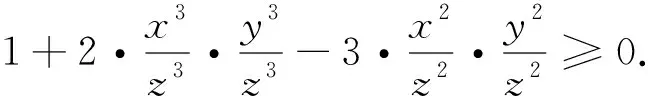
评注:齐次式“降次”法是高次多项式能够分解因式的一个特征，还有常见的“埃森斯坦判别法”等．当需要分解一个齐次式时，一般需要除以单变量次数最高项，再通过代换便可以起到降次的作用．在该题目中，显然除以z6，那么可以将其化为二元不等式，达到降次和简化的目的．

法2以“退”的思路探寻

法3齐次式“减元”法

评注:“减元”法又称为消元法，是解决多元最值或解方程组的核心工具．一切的问题可以归结为数学问题，一切的数学问题可以归结为解方程问题，而解方程的核心思想是减元(消元)．该问题通过减元降低难度，可以很容易进行分解因式，从而问题得到解决．

思路3导数法(通性通法)

解析:先确定主元为“z”，把它视为关于“z”的高次函数来处理，那么问题转化为只需要证明函数f(z)=z6-3x2y2·z2+2x3y3在区间z∈(0,+)上的最小值大于0即可．对f(z)进行求导数，可得f′(z)=6z5-6x2y2z．现在令f′(z)=0，又因为x，y，z>0，那么可得易知在区间上，函数f(z)单调递减；在区间)上，函数f(z)单调递增，故f(z)的最小值当且仅当z2=xy时取等号．同样的思想，可以将原式看成是关于x或y的函数来进行处理，亦可达到相同的效果，此处便不再写出．

评注:导数法是高中解决函数最值或极值问题有效的工具之一．导数法对思维量的要求较低，但是对于逻辑运算的要求相对较高．解决该题目的关键一步是要想到构造函数“f(z)”，并且通过函数“f(z)”的性质，进一步来研究和判断此不等式所具有的性质．

思路4利用重要不等式法

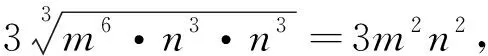
评注:重要不等式是解决不等式的恒成立的强大工具，特别是多元函数的最值问题．我们通过化简得到m6+2n3-3m2n2≥0，观察这个不等式的三项系数，容易发现，系数有规律可循，将-3m2n2移到不等式右边变为3m2n2，而前面显然可以拆成三项之和，故可以想到三元算术——几何均值不等式，从而问题得解．

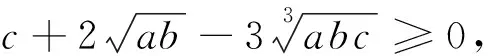
对于问题1的一题多解．对于追求结果来说，一个解法足够，但是一题多解具有多角度审视问题，深层次理解问题的本质，用一个问题沟通了不同的知识体系，有助于形成优化的知识认知结构．本题目具有良好的教育价值，不能仅仅停留在对该问题的解决上，更应该进一步的挖掘隐藏在更深层次的数学内涵和本质，那么我们考虑对问题1进行推广．

3.问题的推广

“一个好的数学老师，往往是一个善于把问题推广的老师”．对于一个问题，用多种方法来解决往往还是不够的，我们接触更多的是它的“变异”形式，即同一个人穿上不同的“马甲”．那么对问题进行推广就有助于我们识别“马甲”背后的数学内涵和本质．

证明推广之前，我们先来看一个引理[1]：

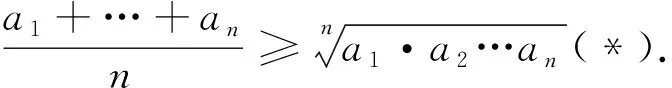
由伯努利不等式可知：当x>-1，n为正数时：(1+x)n≥1+nx恒成立，将其改为参数形式有an≥nλn-1a-(n-1)λn(**)，其中a，λ>0，n∈N+，n>1．