2018年高考数学全国卷Ⅲ理科11题研究

四川省安岳教师进修学校 (642350)

罗 家

云南省昆明市西山区粤秀中学 (650011)

舒前银

2018年高考数学全国卷Ⅲ理科第11题：

这道试题以直观想象、逻辑推理和数学运算等核心素养立意，其思路宽、解法多、可推广，富含思维价值，值得研究.

一、试题解法探究

G.Bolya在《数学的发现》序言中说“数学的首要任务就是加强解题训练”，同时G.Bolya还曾说过“掌握数学就意味着善于解一些要求独立思考，思路合理，见解独到和有发明创造的题.”由此可见，解题研究在数学活动中占十分重要地位.而解法研究是解题研究的主要内容.对高考试题的解法研究可以从一题多解入手.

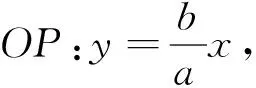
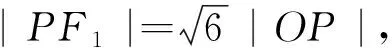
评析:本法主要利用双曲线的渐近线、直线的位置关系、点与点距离公式、双曲线a,b,c的几何性质进行解答，解题思路显而易见，但计算量相对比较大.

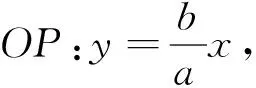
|PA|×c=ab.

图1

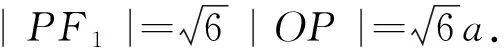
图2

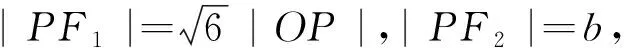
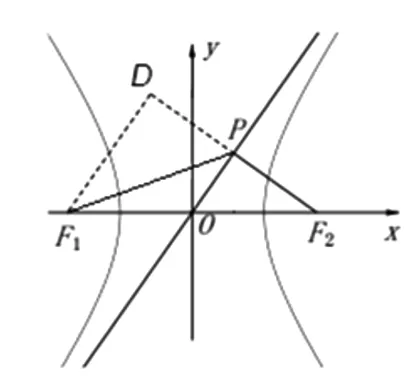
图3

解法四：由解法二可知,|PF2|=b,|OP|=a,过F1作F2P的垂线，交F2P的延长线于D，则OP为中位线.

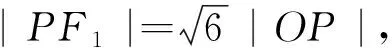
评析:上述三种解法重点利用双曲线的渐近线、几何性质、数形结合思想等，在考查离心率问题时，如果没有给出a,b,c具体的值时，在解答过程中可将a,b,c中任意一个设为具体的特殊值，可以大大简化计算.

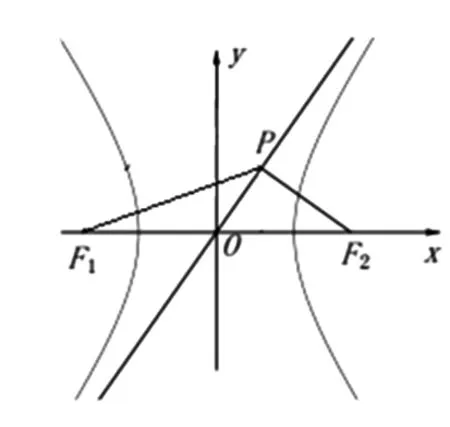
图4

解法五：由解法二可知，|PF2|=b,|OP|=a,

在Rt△OPF2中，因为

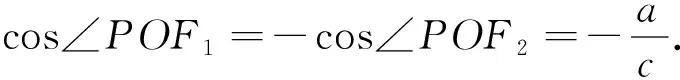
评析:此法仍利用双曲线的渐近线、几何性质，表示出△F2PF1三边及|F1F2|边上中线的长，不难联想到解三角形问题，利用直角三角形中三角函数的定义、诱导公式及余弦定理，建立a,c的方程，进而得到离心率.

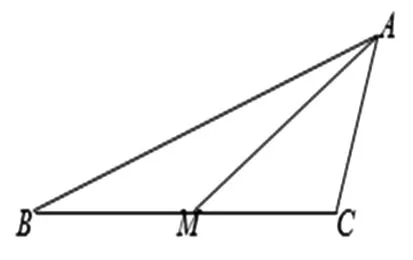
图5

解法六：引理(中线定理又称阿波罗尼奥斯定理)：在ABC中，设M是BC的中点，AM为中线，则|AB|2+|AC|2=2(|AM|2+|MC|2).

图6

评析:此法仍利用双曲线的渐近线、几何性质，表示出△F2PF1三边及|F1F2|边上中线的长，进而想到了中线定理(pappus定理),直接利用定理大大简化了计算.

二、试题的推广

证明:由解法二可知|PF2|=b,|OP|=a,

|PF1|=λ|OP|=λa,由中线定理可得|PF1|2+

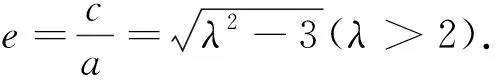
证明:由解法二可知|PF2|=b,|OP|=a,

|PF1|=λ|PF2|=λb.

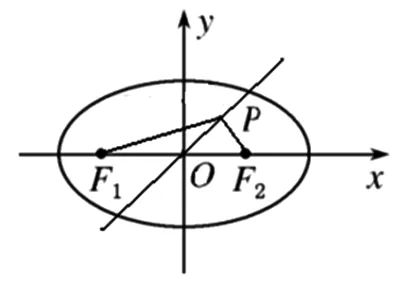
图7

证明:由点到直线的距离公式可得|PF2|=

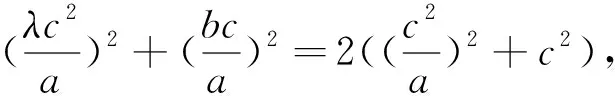
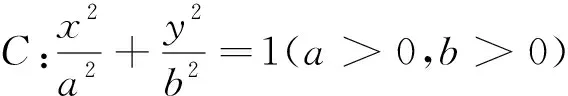
图8