基于距离误差的机器人参数辨识模型与冗余性分析

2018-12-04申景金郭家桢MASOUDKalantari

农业机械学报 2018年11期

申景金郭家桢 MASOUD Kalantari

(1.南京邮电大学自动化学院，南京 210023； 2.国民油井华高公司高新技术部，卡尔加里 T2P 3G3)

0 引言

机器人运动学误差是指由零件加工误差、装配误差等造成的机器人关节实际轴线方位和名义方位之间的差异。根据误差辨识方式的不同，机器人运动学参数辨识可分为开环辨识法、闭环辨识法和关节轴直接测定法[1-4]。其中，开环辨识法基于误差模型，以多个位形下机器人末端位姿误差为目标函数，运用优化算法实现机器人参数辨识。在辨识过程中，若直接利用末端的绝对位置误差和角度误差，会涉及位姿误差在测量坐标系和机器人基坐标系之间的转换，降低了参数辨识的精度[5]。为避免坐标系之间的变换，可采用具有坐标系不变性的距离误差。文献[6-9]分别把距离误差引入到DH模型、MDH模型、DH/MDH模型、加法型指数积模型，对机器人的运动学参数进行了辨识。为实现有效辨识，辨识参数须满足完备性、比例性和连续性原则[10-11]。但是，对于距离误差辨识方法，辨识参数冗余性方面的研究还相对匮乏[12-14]。

本文利用关节旋量的空间几何特性，建立机器人的伴随变换型距离误差模型，使得辨识后的关节旋量自动满足物理约束条件。在此基础上，基于辨识雅可比矩阵的零空间，分析不同距离误差测量方式下可辨识参数的冗余性。最后，通过实验对距离误差模型的有效性和参数冗余性分析的正确性进行验证。

1 伴随变换型误差模型

1.1 正运动学模型

对于n自由度串联机器人，令i和θi分别为转动关节i的运动旋量和转动角度，则有

(1)

其中

vi=qiwi

式中O1×3——1行3列零矩阵

vi——关节量矩

qi——关节轴线上任一点坐标

对于转动关节，wi和vi须满足物理约束条件

(2)

基于指数积形式机器人正运动学模型表示为

gst=ee…egst0

(3)

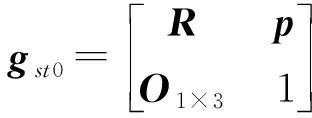
(4)

式中R——末端坐标系相对于基坐标的旋转矩阵

θi——转动关节i的转动角度

p——末端坐标系原点在基坐标系的坐标

gst、gst0——当前位形和初始位形下机器人末端相对于其基坐标系的位姿矩阵

1.2 关节旋量的误差补偿

(5)

(6)

式中 Δξ——关节运动旋量实际值和名义值差值

Ade——旋量对应的伴随矩阵(图1)与加法方法相比，伴随变换方法通过刚体变换把和联系起来，不仅具有明确的物理意义，而且保证旋量自动满足式(2)[15]。此时，对关节旋量的补偿即为确定旋量

图1 关节旋量的伴随变换误差补偿Fig.1 Error compensation of joint screw using adjoint transform

由旋量理论可知：η∈se(3)，se(3)为特殊欧氏群SE(3)的李代数。由于se(3)部分旋量元素构成的子空间N(ξn)对伴随变换补偿无效，为剔除误差模型中的冗余参数，令η可取得有效子空间为Σ(ξn)，则有

N(ξn)⊕Σ(ξn)=se(3)

(7)

(8)

(9)

其中

式中qn——关节轴线上某一点的坐标

η=BK

(10)

其中

确定K中的4个系数即可实现对关节旋量的补偿。

1.3 线性误差模型

为得到线性误差模型，对式(3)线性化可得

(11)

(12)

((δe)e)∨=

(13)

其中

(14)

sai=sinaicai=cosaiai=‖wηi‖

(15)

把式(15)代入式(11)，同时对等号右侧的末端初始位姿项进行与关节旋量相同的分析，可得机器人线性误差模型

(16)

其中δηi=BiKiδηst=BstKst

由于关节转动角度误差δθi可用关节旋量误差表达，因此δθi和δηi不能同时通过式(16)进行辨识[17]。后续的分析中，把δθi误差归结于δηi的误差中。为方便表达，把式(16)写成

(17)

其中Qi=Adi-1-AdiQs=Adn

机器人末端点位置的误差dq可表达为

(18)

2 距离误差模型和参数冗余性分析

2.1 距离误差模型

距离误差表示机器人运动过程中末端点的实际运动距离与名义距离之间的偏差。对任意两个位形，末端点的距离误差δl与其位置误差之间存在如下关系[18]

(19)

把式(19)代入式(18)，dq2-dq1可具体表达为

其中

(20)

(21)

若r为机器人转动关节的个数，通过对雅可比矩阵奇异性的分析，文献[19]已确定位姿误差模型式(17)可辨识4r+6个参数，位置误差模型式(18)可辨识4r+3个参数。本文将确定采用距离误差时可辨识参数的数目。

2.2 可辨识参数冗余性分析

可辨识参数的冗余性是指辨识参数之间存在线性相关性，使得辨识雅可比矩阵奇异，降低参数辨识的精度。为避免该问题，可通过参数的冗余性分析，在误差模型中预先剔除线性相关的参数。

(1)初始位置参数Kst的可辨识性

由式(17)可得

(22)

显然

此时，初始位置参数的雅可比矩阵为关节旋量雅可比矩阵的线性组合。因此，在距离误差模型中，Kst不可与关节旋量同时辨识。

(2)关节旋量参数Ki的可辨识性

为分析Ki可辨识性，考虑3种不同的距离误差测量方式。

①采用绕对应关节轴线旋转的末端距离误差测量方式，机器人运动到如下位形

(23)

此时，式(21)中雅可比矩阵的元素为

(24)

根据1.2节所述，无效子空间N(ξn)的基向量可作为待求零空间的两个基向量。为确定其余3个基向量，考虑式(10)中B的张成基，可以看到零空间的基矢量ζ为

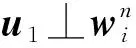
(25)

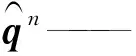
(26)

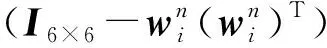
式(25)可简化为

(27)

显然地，零空间的两个基向量可选择为

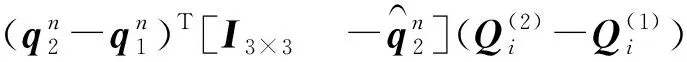
(28)

②为辨识与λ1和λ2相关的参数，对i≥2关节，考虑第2种测量方式，即相对于初始位形测量距离误差

(29)

式(21)中的雅可比矩阵有

(30)

为分析{λ1,λ2}是否位于该种测量的零空间，首先对λ1进行分析。

(31)

(32)

其中

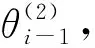
(33)

③为辨识与κ相关的参数，考虑第3种测量方式，即

(34)

(35)

3 实验验证

为验证所建立的距离误差模型的有效性和辨识参数冗余性分析的正确性，利用三维扫描仪和5自由度KUKA youBot机器人搭建实验平台(图2)。通过点云处理和数据分析后，扫描仪的对齐误差精度小于0.02 mm，远高于KUKA youBot运动精度，满足机器人标定的要求。另外，通过误差统计分析，确定了忽略高阶误差项的线性模型可实现对KUKA youBot机器人运动学参数的有效辨识[21]。

图2 机器人标定实验平台Fig.2 Experiment platform of robot calibration1.KUKA youBot机器人 2.天远三维扫描仪 3.控制器 4.计算机点云处理及配套软件

为验证辨识参数冗余性分析的正确性，分别采用第1种测量方式和第2种测量方式生成20个机器人运动位形。在第1种测量方式的每次测量过程中，只有一个驱动关节，其余关节为锁定状态。在随机生成驱动关节对应于参考位形和驱动位形的角度后，通过测量机器人末端从参考位形运动到驱动位形的相对位移，来完成一次测量。从基关节开始，全部关节依次被设定为驱动关节。对每一个驱动关节，分别测量4组不同位形下的机器人末端运动位移。在第2种测量方式的每次测量过程中，两个相邻的关节为驱动关节，其余关节为锁定状态。与第1种测量方式的参考位形可变不同，第2种测量方式的参考位形保持为机器人的初始位形。对4组不同的驱动关节，分别测量5组不同位形下的末端位移。将测量数据和不同位形的关节角代入式(21)，即可确定机器人的距离误差模型。通过对误差模型中雅可比矩阵的特征值分析，发现在2种测量方式下，雅可比矩阵的秩分别为10和14，这与冗余性分析结果相一致。

在实际辨识时，为得到较好的辨识效果，一般随机产生大量的机器人运动位形，从中选择所构成的雅可比矩阵中特征值较大的行所对应的位形，作为辨识位形。本文实验过程中，在随机生成的100个不同运动位形中，选择了32个特征值较大的位形用于机器人的运动学参数辨识。此时，把实验数据代入式(19)，通过辨识雅可比矩阵的奇异值分解，发现可辨识参数的个数为18，验证了距离误差模型所辨识参数最多为4r-2。

基于距离误差模型和实验数据，采用最小二乘法对机器人运动学参数进行迭代求解。图3给出了测量位形上距离误差最大值、平均值和迭代步数之间的关系。经过3次迭代之后，机器人参数收敛到稳定值(表1)。图4给出了3次迭代过程中，32个测量位形上的距离误差的变化曲线。所测量位形的距离误差最大值由6.226 mm降低到0.718 8 mm，精度提高了8.7倍，距离误差平均值从2.978 mm降低到0.257 6 mm，精度提高了11.6倍。