基于方位特征方程的2T2R并联机构拓扑综合与分类

孙驰宇 沈惠平， 袁军堂 杨廷力

(1.南京理工大学机械工程学院, 南京 210094； 2.常州大学现代机构学研究中心, 常州 213016)

0 引言

目前，国内外并联机构型综合[1]的方法主要有：基于螺旋理论的方法[2-3]、基于位移子群的方法[4-5]、基于线性变换与进化形态学的方法[6-7]和基于方位特征集(POC)的方法[8-12]。这些理论方法都是以自由度、动平台的输出运动类型和数目为设计目标，通过设计各种支链及其在动、静平台之间的拓扑布置，构造拓扑结构，具有较好的系统性、严密性。但前3种方法需要较好的数学基础，一般工程技术人员较难理解和掌握。基于POC集的方法仅需简单的逻辑运算，每一步都有确定的计算公式或设计准则，简洁明了，易于掌握，有利于发现更多新机构。

4自由度并联机构中的三平移一转动SCARA机构[13-14]已有较多研究与应用，而两平移两转动(2T2R)机构却较少，但该类机构在工业上也有应用潜力，可应用于减振平台、坐标测量机、农业采矿振动筛、脚踝康复装置、结合工作台的运动构成五轴联动数控机床等，因此，对2T2R并联机构进行型综合研究仍具有一定的意义。

陈海等[15]基于螺旋理论提出了两平移两转动完全解耦并联机构构型综合方法；KUMAR等[16]基于螺旋理论对2T2R机构进行了型综合，并综合出简单支链构成的机构，以用于精密医疗器械；YOON等[17]提出了一种双平台3支链的2T2R并联机构；MERLET[18]对2T2R机构型综合进行了论述；LI等[19]依据约束综合方法，综合了一系列对称的2T2R机构；FAN等[20]基于进化形态与李群理论，对2T2R机构进行了型综合；WANG等[21]基于李群理论提出了两种具有较高转动能力的2T2R机构；杨廷力等[10]基于POC方法，综合了一部分2T2R机构。本文在文献[10]的基础上，通过设计新的HSOC(混合支链)，设计10种新型2T2R构型。同时，依据支路结构和动平台数目，对综合出的机构进行分类，并对它们进行拓扑特征分析，得到其所包含的AKC、耦合度数、自由度类型和运动解耦性。

1 基本理论

为便于理解，给出基于POC方程的并联机构拓扑结构设计理论和方法[10]。

1.1 串联机构的POC方程

串联机构 POC方程为

(1)

式中MS——串联机构末端相对于定平台的POC集

m——运动副数

MJi——第i个运动副的POC集(表1)

Msub-SOCj——第j个子单开链(sub-SOC)的POC集

表1给出了仅包含R副与P副的12种sub-SOC及其POC集。

1.2 并联机构的POC方程

并联机构POC方程为

(2)

式中MPa——并联机构动平台的POC集

Mbj——第j条支路末端构件的POC集

ν——独立回路数

由式(2)可知，PM支路的POC集Mbj应满足

Mbj⊇MPa (3)

注: 标有*者，表示末端构件的基点o′不在运动副轴线上。

1.3 机构DOF公式

机构DOF公式为

(4)

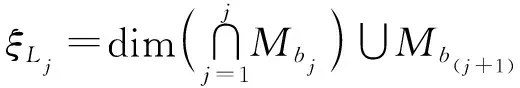
式中F——机构自由度

fi——第i个运动副的自由度

ξLj——第j个独立回路的独立位移方程数

Mbj——第j条支路末端构件的POC集

1.4 并联机构型综合的一般过程

并联机构拓扑结构设计的一般过程，见文献[11]。

2 2T2R并联机构的拓扑结构综合

依据上述基本理论，给出2T2R并联机构的型综合过程和方法，并得到15种2T2R机构，其中10种为本文综合得到。

设计要求：设计4自由度2T2R的并联机构，且每条支链仅含一个驱动副，包含的P副只能为驱动副。即机构动平台实现的POC集为

2.1 确定支路的POC集

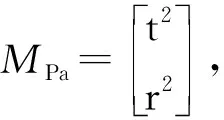
2.2 支路的结构综合

2.2.1单开链(Single open chain, SOC)支路的综合

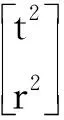
(1)确定SOC支路的基本功能

② 支路的自由度为4，即F=dim{MS}=4。

(2)确定运动副的组合方案

由条件公式[21]

(5)

式中F1——支路自由度

mR——转动副数目

mP——移动副数目

dim{MS(r)}——支路POC集独立转动元素数

dim{MS(t)}——支路POC集独立移动元素数

且已知：dim{MS(r)}=2，dim{MS(t)}=2，可得：mR≥2,mP≤2。

再由串联POC方程(式(1))及表1，可得运动副的组合方案为3种：4R、3R1P、2R2P。

(3)确定SOC支路包含的sub-SOC，并生成SOC支路

①方案1: 4R

由dim{MS(r)}=2及式(1)与表1之2可知，该支路可由一个sub-SOC{-R‖R‖R-}及一个R副串联而成，得到支路SOC{-R‖R‖R-R-}，其基点o′位于末端R副轴线上。

②方案2: 3R1P

由dim{MS(r)}=2及式(1)与表1之2可知，该支路可由一个sub-SOC{-R‖R⊥P-}及一个R副串联而成，得到支路SOC{-P⊥R‖R-R-}，其基点o′位于末端R副轴线上。

③方案3: 2R2P

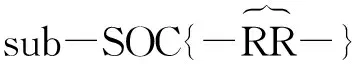
从造字上看，“葬”字为会意字，本义为上下藉以草、中间为尸身。《易·系辞下》：“古之葬者，厚衣之以薪，葬之中野，不封不树。”所以，上文提到的皇甫谧苇席裹尸应该是最原始意义上的葬式。杨王孙要求“死则为布囊盛尸，入地七尺，既下，从足引脱其囊，以身亲土”(《汉书·杨王孙传》)，这种裸葬的方式倒是比较新奇，也是最为直接的“入土为安”。其实，庄周、杨王孙和皇甫谧这些抗俗者都是比较激进的矫俗者，主要是在行为上更加标新立异和惊世骇俗。东汉范冉在《遗令敕子》中说：“吾生于昏暗之世，值乎淫侈之俗，生不得匡时济世，死何忍自同于世！”[15](P656)可以看做是激进抗俗者的心声流露。

(4)检验支路的POC集

由式(1)可知，以上3种方案所得的3条单开链支路都满足该支路的POC设计要求。

例如：SOC{-P⊥R‖R-R-}支路由sub-SOC{-R‖R⊥P-}及一个R副串联而成，将它们的POC集代入式(1)，可得该支路的POC集

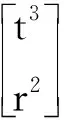
确定各SOC支路所包含的sub-SOC，并生成SOC支路的POC集。

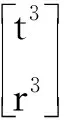
易知，满足该POC集要求的支路结构有SOC{-S-S-R-}、SOC{-S-P-S-}等。

2.2.2复杂单开链(Hybrid single open chain, HSOC)支路的综合

当一条SOC的POC集与一子并联机构(sub-PM)末端的POC集完全相同时，称它们拓扑等效。HSOC支路综合就是一个将SOC支路替换为拓扑等效的sub-PM的过程。表3给出常用的sub-PM类型及与其对应的拓扑等效SOC，以便于HSOC支路的综合。

由表3及2.2.1节所综合出的SOC支路可得10种HSOC种支路。其中，(2T-2R)HSOC结构有3种，如图1所示；(3T-2R)HSOC结构有5种，如图2所示；(2T-3R)HSOC结构有2种，如图3所示。

为便于比较，表2列出了2.2.1节中叙述的12种SOC支路构型，并根据本节HSOC支路综合方法,衍生出10种HSOC支路构型，其中(3)、(7)、(8)、(9)、(10)为5种新构型HSOC结构。

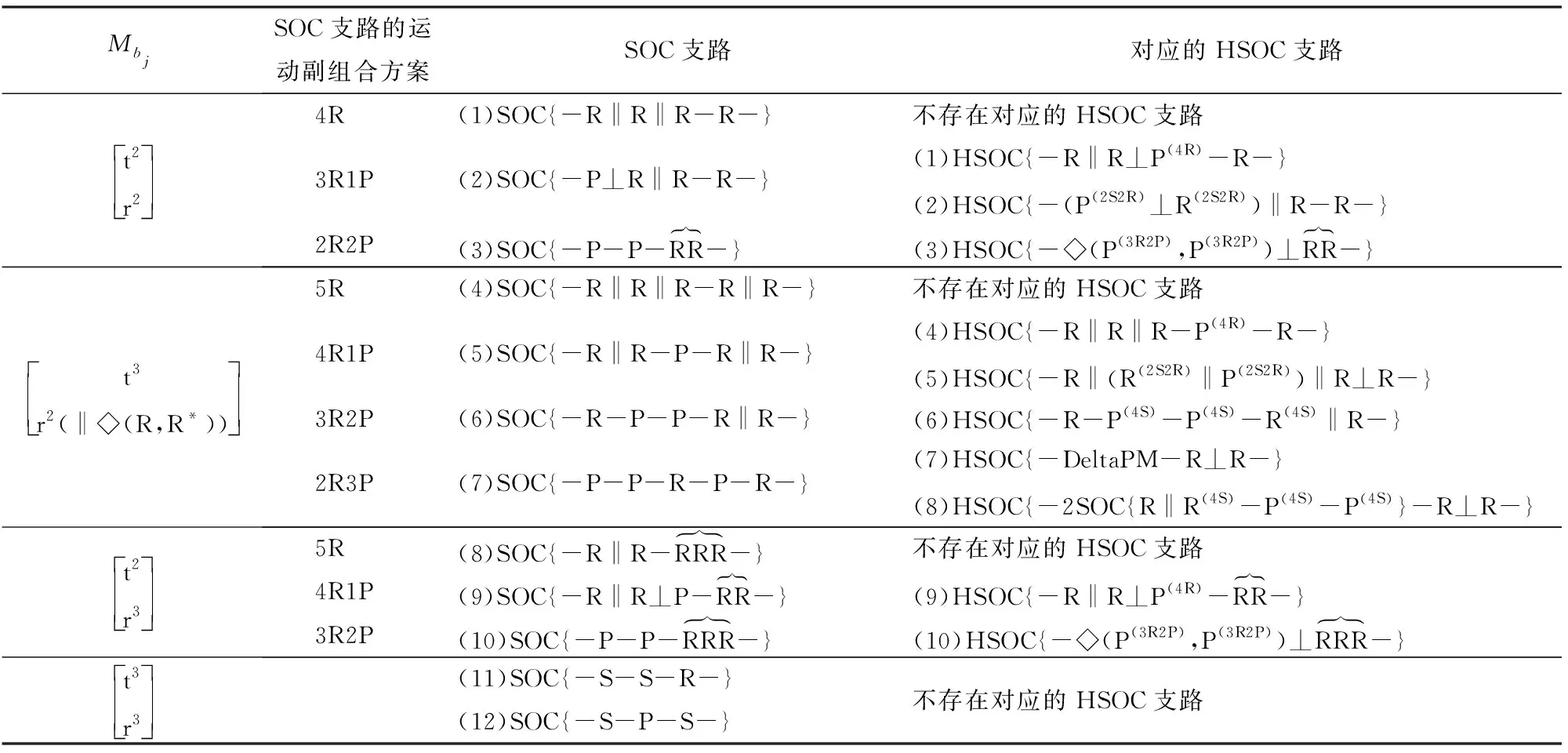
表2 SOC支路与HSOC支路的结构类型Tab.2 Branch structure types of SOC branch and HSOC branch

表3常用的sub-PM及其拓扑等效SOC
Tab.3Frequentlyusedsub-PMandtheirtopologicalequivalenceSOC

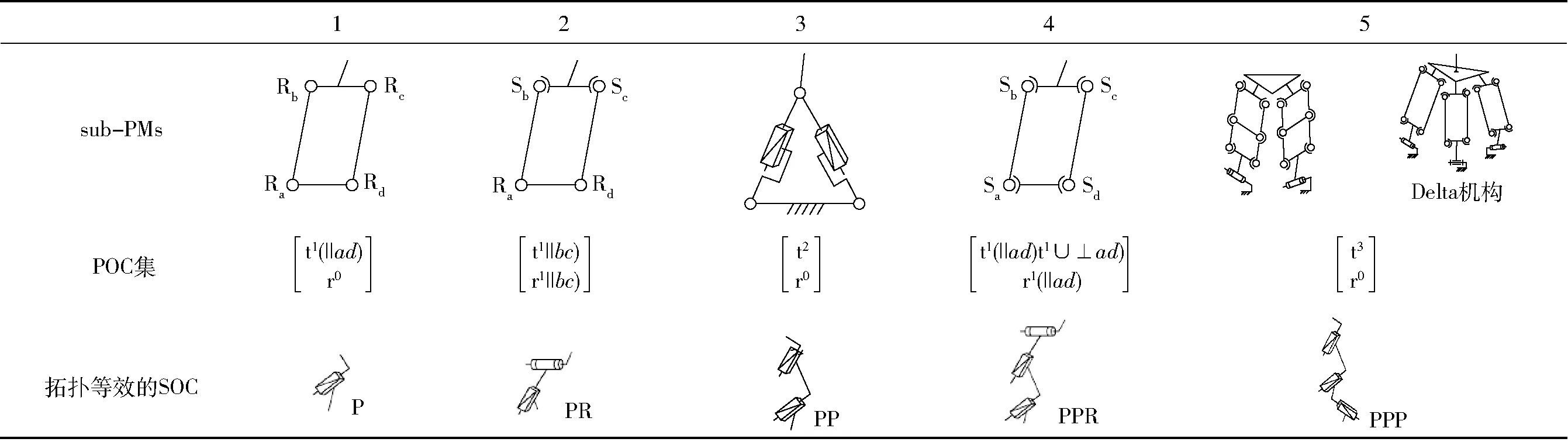
注: 表中No.4之sub-PM的4个S副，应保持平行四边形。

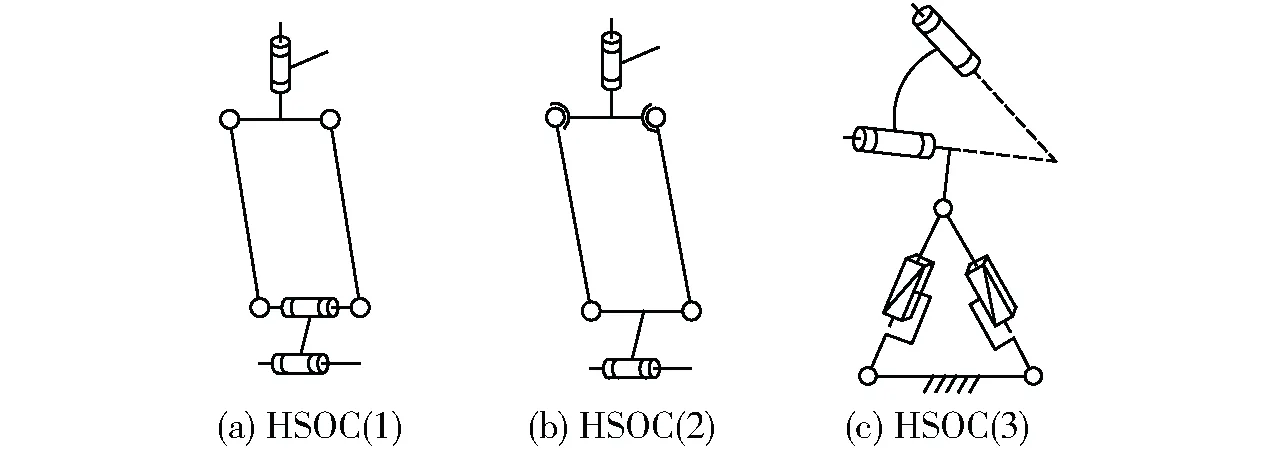
图1 (2T-2R)支路的3种结构类型Fig.1 Three types of (2T-2R) branch structure

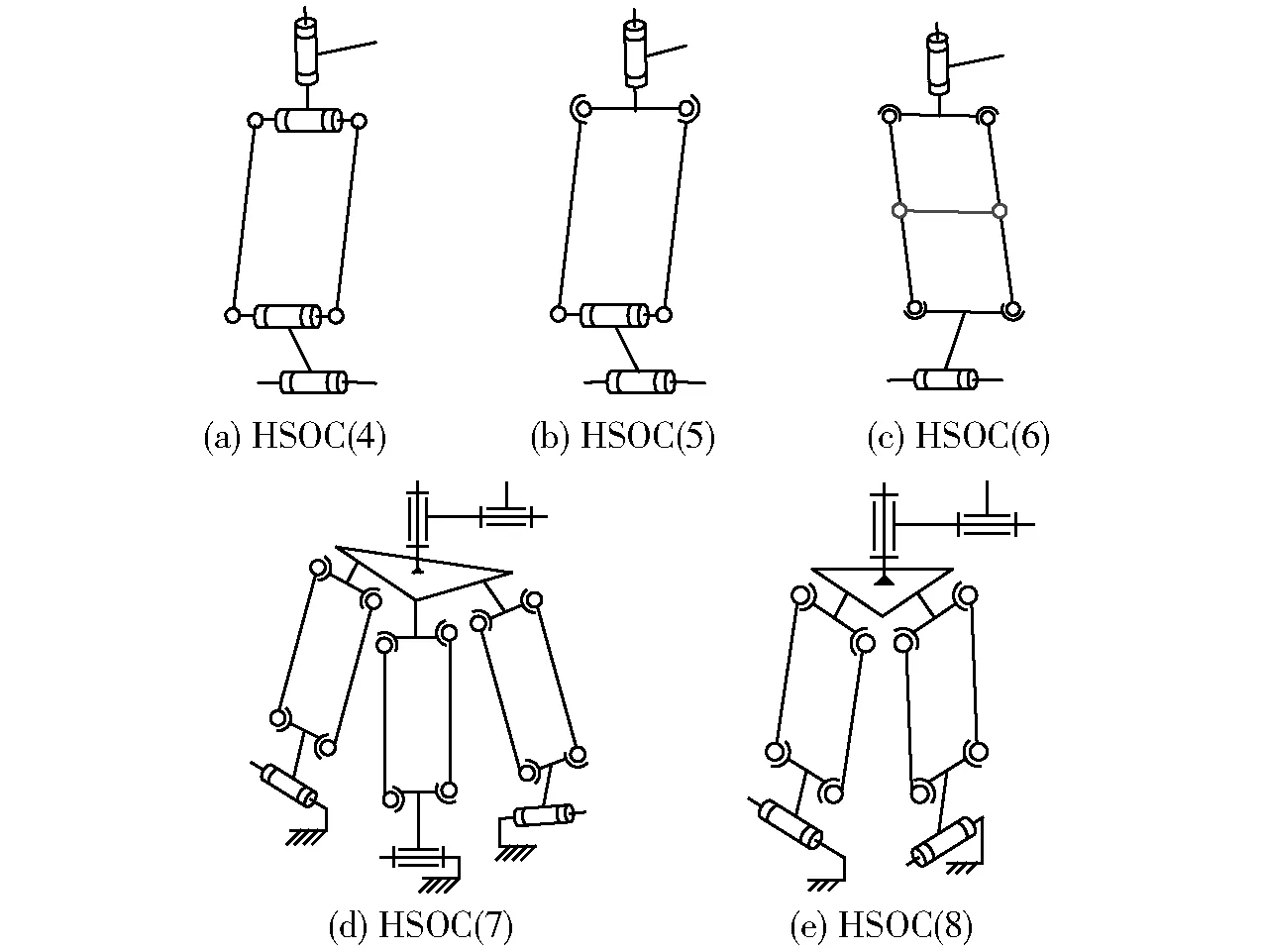
图2 (3T-2R)支路的5种结构类型Fig.2 Five types of (3T-2R) branch structure

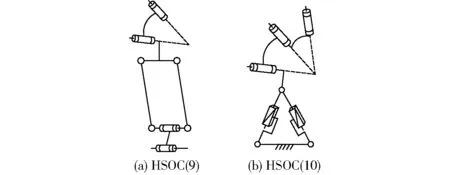
图3 (2T-3R)支路的2种结构类型 Fig.3 Two types of (2T-3R) branch structure

2.3 确定支路组合方案

由表2可得4种不含P副SOC支链结构(表2中SOC(1、4、8、11))以及10种HSOC支链结构，对它们进行组合以综合出满足POC集要求的2T2R并联机构，其中，考虑到每条支链应只含一个驱动副且所用驱动副皆处于同一平面，本文给出表2中部分支链组合结果的15种方案，如表4所示。

2.4 确定支路装配几何条件

由式(3)可知，综合出的并联机构的POC集所包含的元素,应多于或至少等于支链的POC集，因此，可运用支链间POC集交集运算，可以消去支路POC集中并联机构所不包含的POC集元素，现给出支路交运算的基本公式，以此可确定装配的几何条件。分为转动、移动两种情况：

转动元素：当满足式(6)～(8)中上式右侧的几何条件时，左侧的交集运算可不约束掉转动元素，POC集保持不变；当满足式(6)～(8)中下式右侧的几何条件时，左侧的交集运算将约束掉一个转动元素。

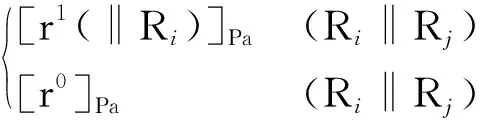
(6)

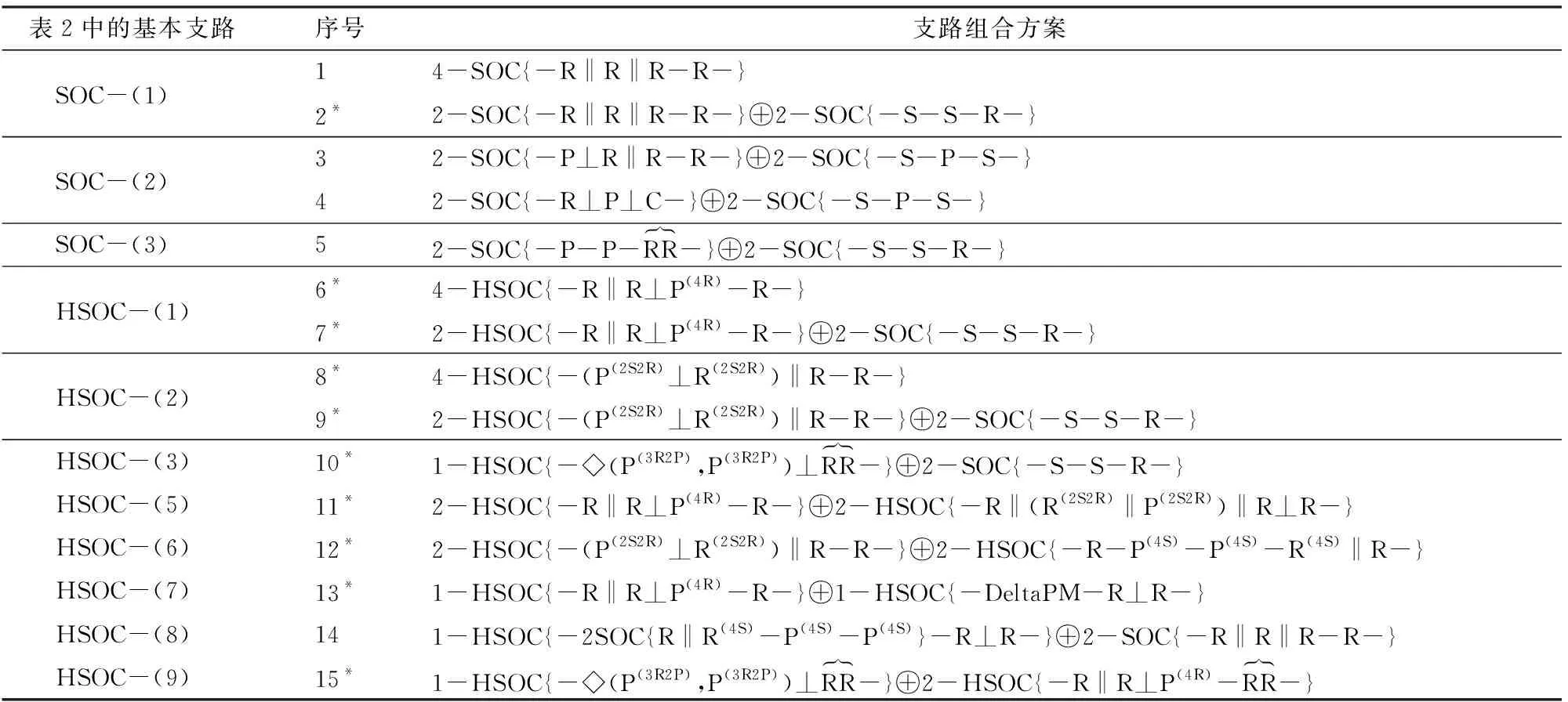
表4 (2T-2R) PM的支路组合方案Tab.4 Branch combination schemes of (2T-2R)PM

注: 标有*者，为本文首次提出的新机构。

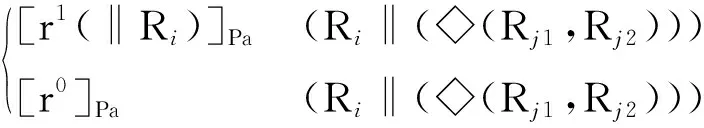
(7)

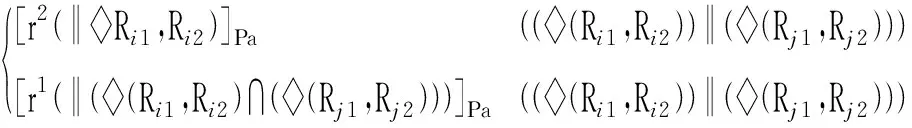
(8)

移动元素：当满足式(9)～(11)中上式右侧的几何条件时，左侧的交集运算可不约束掉移动元素，POC集保持不变；当满足式(9)～(11)中下式右侧的几何条件时，左侧的交集运算将约束掉一个移动元素。

(9)

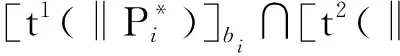
(10)

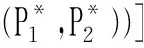
(11)

以表4中序号1的支路为例，确定其动定平台间的几何装配条件。

已知该机构4条支路结构相同，皆为SOC{-Rj1‖Rj2‖Rj3-Rj4-},j=1,2,3,4。基点o′为R14轴线上一点。

由2.2节可知，当基点取在末端R副轴线上时，该支路的POC集为

基点取在轴线外位置时，该支路的POC集为

将期望的并联机构动平台POC集及各支路的POC集代入并联机构POC集方程中(式(2))，可得

符号“⟸”表示式中右端所有支路POC集交运算得预期目标为左端的POC集。

为实现动平台输出为2T2R，各条支路POC集交运算后需约束掉一个移动元素，且POC集的转动元素保持不变。由式(8)的上式逆运算可知：其装配几何条件为:R11‖R21‖R31‖R41, R14‖R24‖R34‖R44，且基点取在R14与R24的共线轴线上。按此装配几何条件得到的并联机构，如图4a所示，对应表4的序号1，该机构由4条相同的简单支链构成，见文献[10]。进一步，已知第1、2条支路POC集交运算已满足2T2R的型综合要求，即第3、4条支路可为包含2T2R方位特征集的无约束简单支路结构，如3T3R的SSR结构等，如图4b所示，对应表4的序号2。

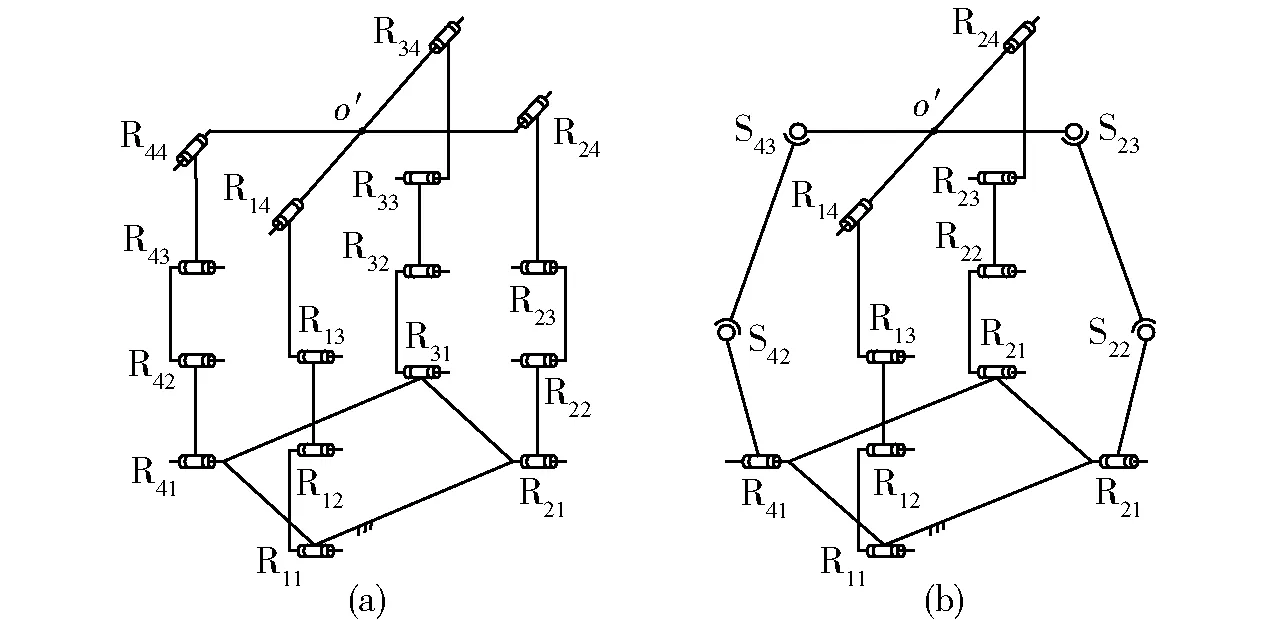
图4 SOC-(1)的两种(2T-2R) PMFig.4 Two types of (2T-2R) PM structure composed by SOC-(1)

按照上述步骤，现分别确定表4中其他支路组合方案的几何条件，得13种并联机构，如图5～12所示，简述如下：

(1) 按表4中第3、4组合方案综合出的并联机构，如图5所示，其中图5a机构中R11‖R13‖R21‖R23；P12⊥R11；P22⊥R21；R14与R24轴线共线且基点取在轴线上，该机构由4条简单支链构成[10]。第4方案(图5b)实为第3方案的变形，将R13与R23移除，同时将R14与R24在同样位置上替换为2个C副，该机构由FAN等[20]提出，该文使用运动副替代的思想提出了类似的一系列包含C副、U副的简单支链构成的2T2R机构。

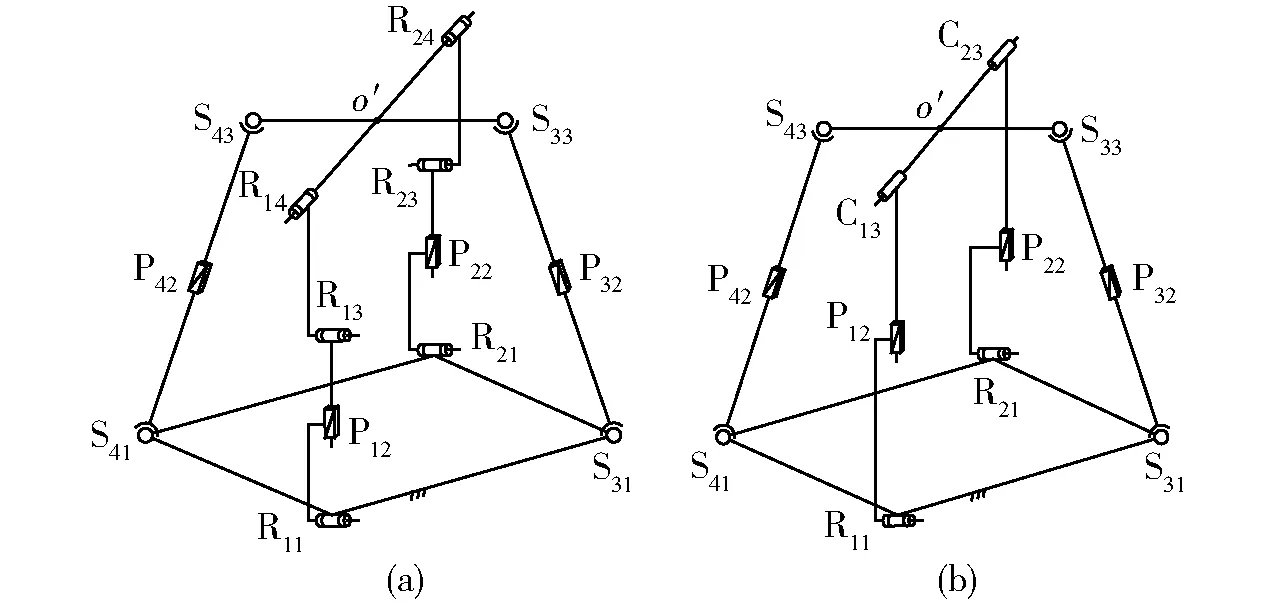
图5 SOC-(2)的一种(2T-2R) PM及其变形Fig.5 (2T-2R) PM structure composed by SOC-(2) and its metamorphosis

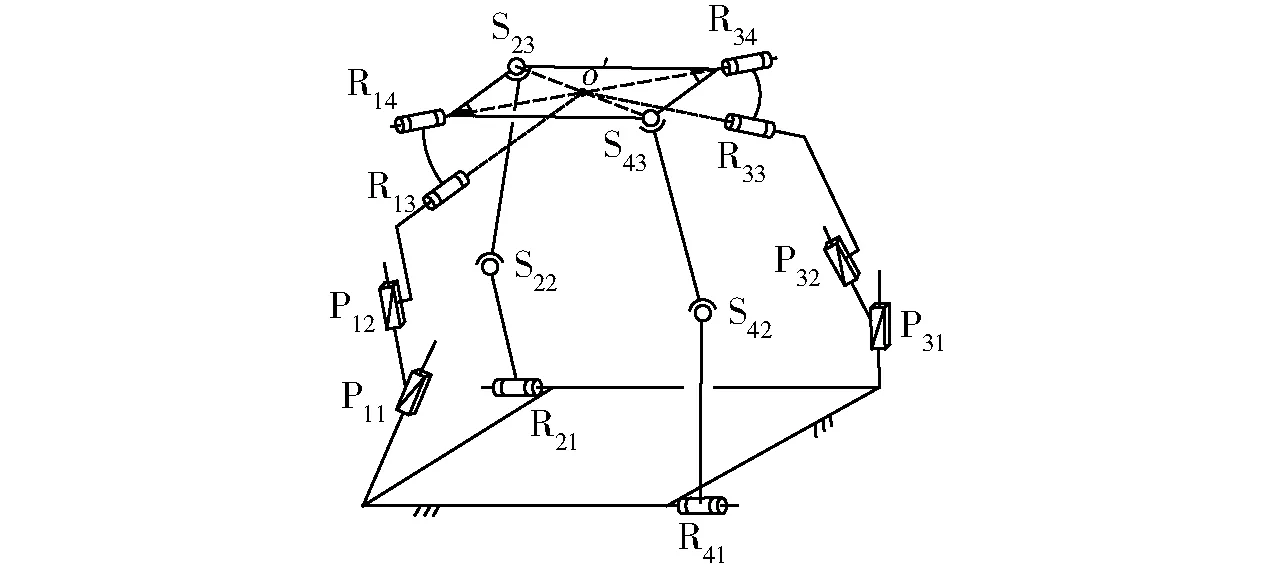
图6 SOC-(3)的一种(2T-2R) PMFig.6 (2T-2R) PM structure composed by SOC-(3)

(2)按表4中第5组合方案综合出的并联机构，如图6所示，其中，P12与P12共面且垂直于R13；P31与P32共面且垂直于R33；R14与R34共线且基点为4个R副轴线交点。该机构由KUMAR等[16]提出，其4条支路都为简单支链，结构较为简单。

(3)按表4中第6、7组合方案综合出的并联机构，如图7所示，其中图7a机构中R11‖R12‖R21‖R22‖R31‖R32‖R41‖R42；R13‖R23‖R33‖R43；R13与R23轴线共线且基点取在轴线上。图7b机构将图7a机构的第3、4条支链替换为SSR结构，且定平台4个R副平行。

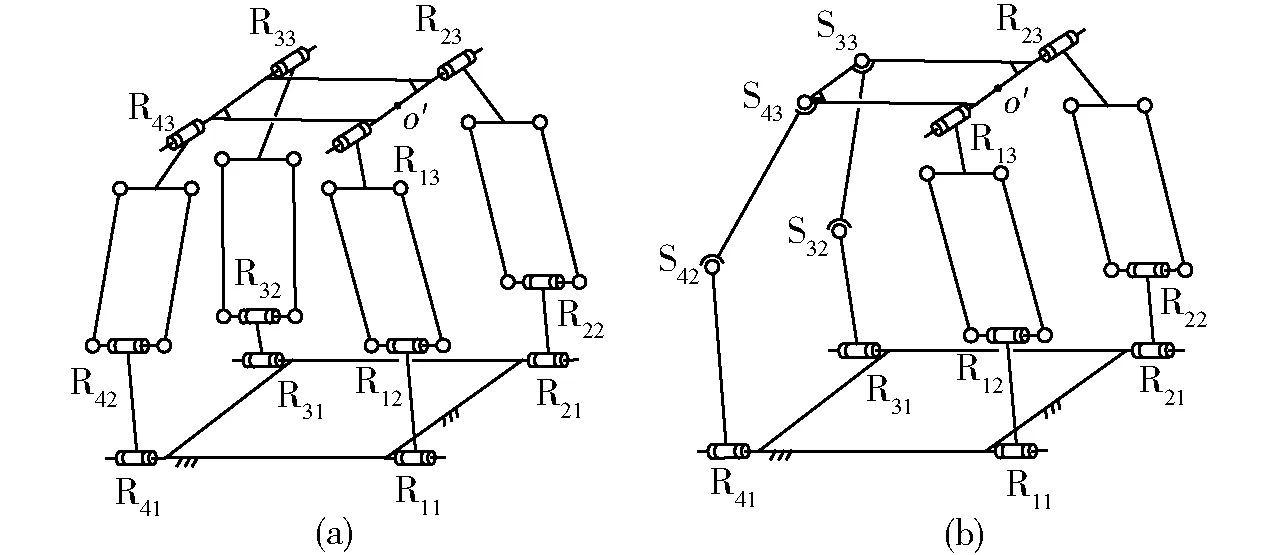
图7 HSOC-(1)的两种(2T-2R) PMFig.7 Two types of (2T-2R) PM structure composed by HSOC-(1)

(4)按表4中第8、9组合方案综合出的并联机构，如图8所示，其中，图8a定平台上4个R副平行，动平台上4个R副也平行，基点位于动平台两R副共线轴线上。图8b将图8a机构的第3、4条支链替换为SSR结构，且定平台4个R副平行。

图8 HSOC-(2)的两种(2T-2R) PMFig.8 Two types of (2T-2R) PM structure composed by HSOC-(2)

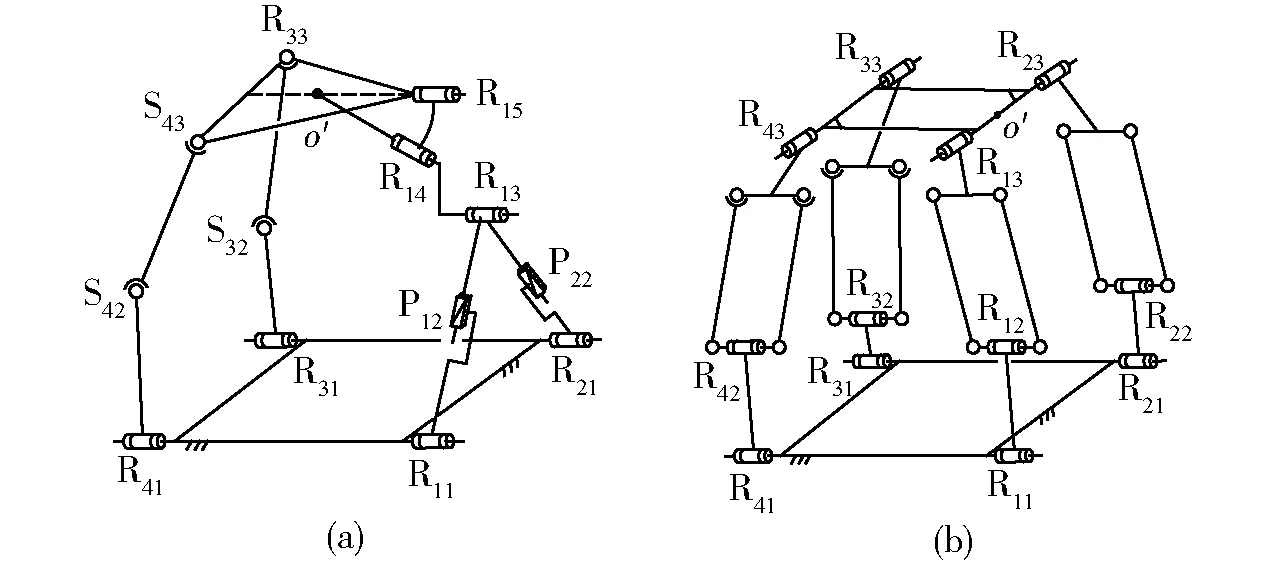
图9 HSOC-(3)及HSOC-(5)的 (2T-2R) PMFig.9 (2T-2R) PM structure composed by HSOC-(3) and HSOC-(5)

(5)按表4中第10、11组合方案综合出的并联机构，如图9所示，其中图9a机构中R11‖R21‖R13‖R31‖R41；P12⊥R11；P22⊥R21；基点位于R14与R15轴线的交点。图9b机构中R11‖R12‖R21‖R22‖R31‖R32‖R41‖R42；R13‖R23‖R33‖R43；R13与R23轴线共线且基点取在轴线上。

(6)按表4中第12、13组合方案综合出的并联机构，如图10所示，其中，图10a定平台上4个R副平行，动平台上4个R副也平行，基点位于动平台两R副共线轴线上。图10b中R11‖R12‖R22；R13⊥R11；R13与R23轴线共线且基点取在轴线上。

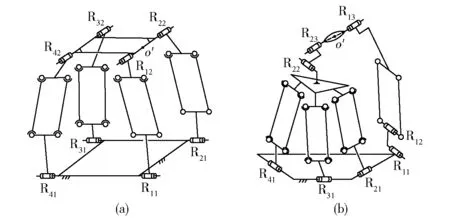
图10 HSOC-(6)及HSOC-(7)的(2T-2R) PMFig.10 (2T-2R) PM structure composed by HSOC-(6) and HSOC-(7)

(7)按表4中第14组合方案综合出的并联机构，如图11所示，其中R11‖R12‖R13‖R21‖R22‖R23‖R32；R14‖R24‖R33；R14与R24轴线共线且基点取在轴线上。它由WANG等[21]提出，该机构具有较强的转动能力。

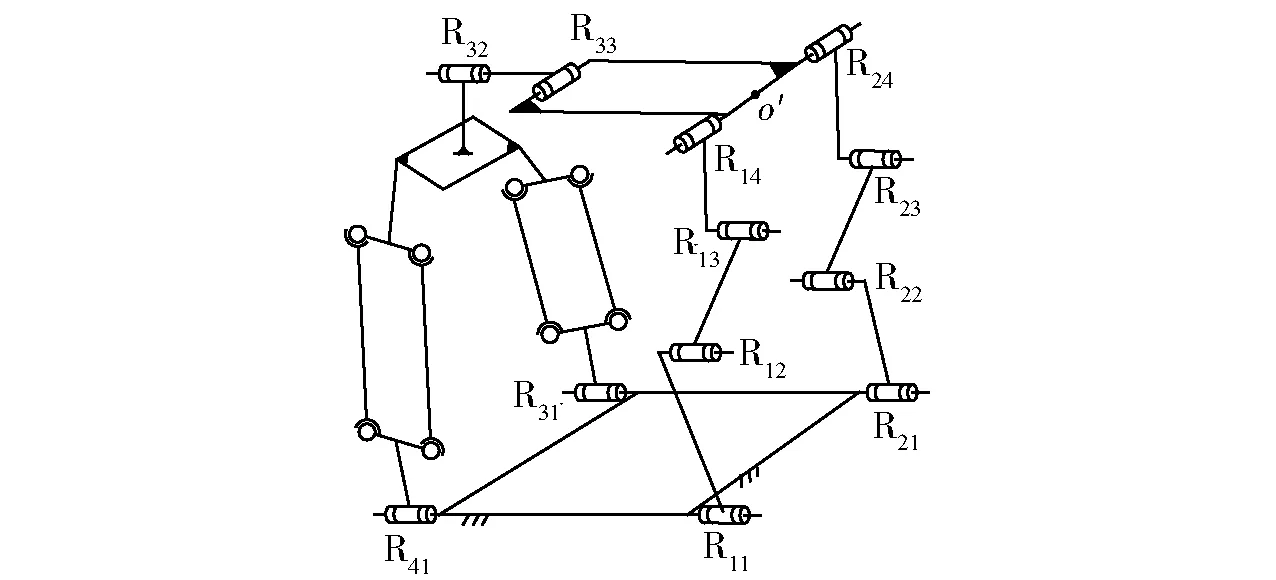
图11 HSOC-(8)的 (2T-2R) PMFig.11 (2T-2R) PM structure composed by HSOC-(8)

(8)按表4中第15组合方案综合出的并联机构，如图12所示，其中R11‖R13‖R21‖R31‖R32‖R41‖R42；P12⊥R11；P22⊥R21；R14、R15、R33、R34、R43、R44的轴线交于一点且为基点。

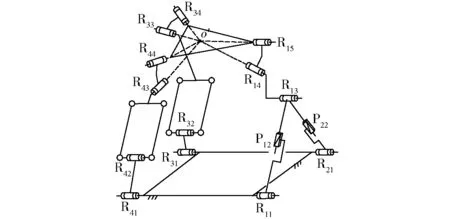
图12 HSOC-(9)的 (2T-2R) PMFig.12 (2T-2R) PM structure composed by HSOC-(9)

2.5 选定机构驱动副

对于自由度为F的机构，在判定其驱动副时[10]，可将预定的F个运动副锁死，此时得到的新机构的自由度若为0，则该F个运动副可同时为机构的驱动副，否则，该F个运动副不能同时为机构的驱动副。

以图4a为例，判定该机构定平台上的4个R副是否可为驱动副。

(1)确定支路拓扑结构

将定平台的4个R副(R11,R21,R31,R41)锁死，得到新的并联机构，其支路拓扑结构为

SOC{-Rj2‖Rj3-Rj4-} (j=1,2,3,4)

(2)确定支路的POC集

由式(1)可得，当基点取在末端R副轴线上时，该支路的POC集为

基点取在周线外位置时，该支路的POC集为

(3)确定新机构的自由度

将各支路末端POC集代入式(4)，并由式(1)、(2)可得

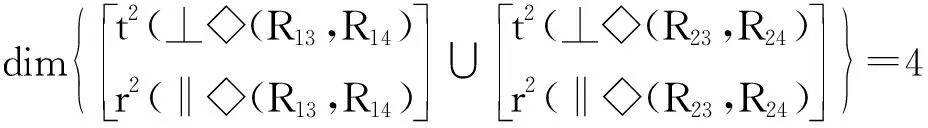
将ξLj代入式(4)，得到新机构自由度为

(4)由于新机构的自由度为0，可得定平台上4个R副(R11、R21、R31、R41)可为4个驱动副，即满足设计要求。

类似地，可用同样方法，判定图4～12所示并联机构的驱动副，都为定平台上4个R副，也都满足设计要求。

以上为本文综合出的15种2T2R机构，详见表5，其中带*的机构为本文首次提出的新机构。

3 2T2R并联机构的拓扑结构分类

3.1 拓扑结构分类

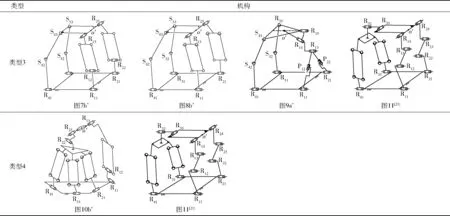
综上所述，现依据支路结构和动平台数目，对综合出的15种2T2R机构(其中10种为新型的2T2R机构)进行如下机构类型分类，详见表5。

其中①皆由简单支路构成的机构(类型1)有5种：即表4中序号1～5。②皆由复杂支路构成的机构(类型2)有6种：即表4中序号6、8、11、12、13、15。③由简单支路复杂支路共同构成的机构(类型3)有4种：即表4中序号7、9、10、14。④单动平台的机构有13种：即表4中序号1～12及序号15；双动平台的机构(类型4)有2种：即表4中序号13、14。

表5(2T-2R)PM的4种类型
Tab.5Fourtypesof(2T-2R)PM

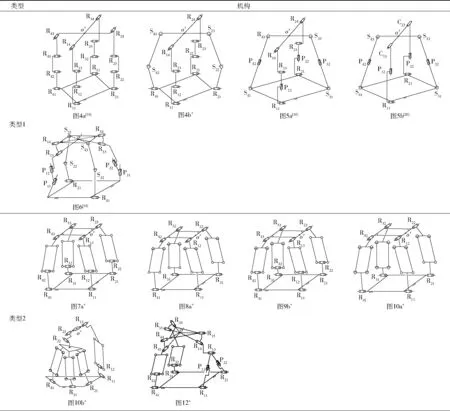
续表5

3.2 拓扑特征分析

为优选具有实用价值的机构，根据文献[10]中提出的拓扑特征计算方法，对表5中的15种2T2R机构进行拓扑特征分析，得到其所包含的基本运动链(BKC)、耦合度(κ)、自由度类型和运动解耦性，详见表6。

表6 (2T-2R) PMs的拓扑特征Tab.6 Topology structure characteristics of (2T-2R)PM

(1)耦合度是衡量机构复杂程度的一种拓扑不变量，对于耦合度为1的机构，一般可用一维搜索法得到位置问题的全部实数解。表6中，耦合度为1的机构为序号10、14、15，其中，序号10与序号15为本文设计的新机构，而本文参考文献中列举的，为已有的其他构型(序号1、3、4、5)，它们的耦合度为2，其机构较为复杂。本文所提新机构与之相比，优点为：耦合度仅为1，机构结构较为简单，较易处理运动学与动力学问题。

(2)运动输入-输出解耦可使机构运动学分析较为简单，又能简化机器人的控制问题，因此，实现运动输入-输出解耦是机构拓扑结构设计的重要目标之一。表6中，部分解耦且具有部分自由度的机构为序号13，该机构为本文设计的新机构，其包含两个BKC，且耦合度分别为1和0，而本文参考文献中列举的，已有的其他构型(序号1、3、4、5、14)，它们仅包含一个BKC，具有完全自由度，且不解耦。

4 结论

(1)基于拓扑等效替代的复杂支路型综合方法，提出了5种HSOC新构型支链。

(2)基于POC方程的并联机构结构综合方法，结合综合出的新型HSOC支链结构，给出了15种2T2R并联机构构型，其中，5种是已有机器人构型，其余10种是具有实用价值的新构型。

(3)依据拓扑结构特性，对综合出的2T2R机构进行分类，其中，皆由简单支路构成的机构5种，皆由复杂支路构成的机构6种，由简单支路、复杂支路共同构成的机构4种；单动平台的机构13种 ，双动平台的机构2种。进一步对综合出的15种机构进行拓扑特征分析，计算其耦合度、自由度类型和运动解耦性，筛选出结构较简单、耦合度为1的机构以及较易于控制的部分解耦机构。