窗格中的数学题

常文武

假日里在花园里漫步，发现长廊的一个正六边形镂空窗非常美觀，它的窗格是规整的正三角形的网格，也许是维修工人临时固定松动木框，优美的窗花上面平添了两条多余的铁丝.如图1.

咦，这倒正好提出一个有趣的数学问题：这两条铁丝所在直线的夹角α是多少度呢？

聪明的你不必马上读下去.先拿起纸笔，试试你的解题功力吧！

如果你在读高中，自然想起两直线夹角的公式：这个解题套路.在图3中，利用平行线内错角相等就可以得到∠1=∠2+∠3.）

至此，我们找到一个不那么死板的解法.但是还是不太令人满意，因为我们需要另证结论.有没有其他办法，又不需要用到高中的知识就能求解此题呢？

回到图1，我们发现通过第二种解法可进一步发现这两条线段其实是等长度的.要想说明两条等长的线段夹角是60°，不如找到一个旋转角为60°的旋转变换，让一条线段经过旋转到达另一条上.有这样的旋转变换吗？

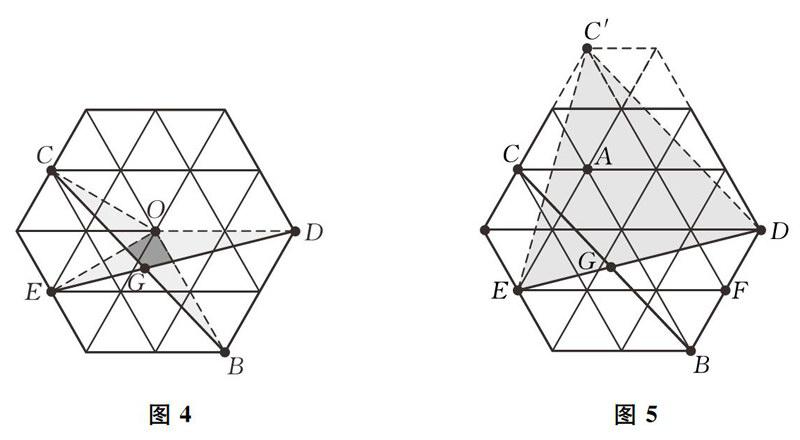
这样的旋转是存在的：如图4所示，假设旋转变换使得C运动到E，同时B运动到D，那么旋转中心就是CE的垂直平分线和BD的垂直平分线的交点.这个点正是窗子的中心点O.不难验证，由于OCE构成等边三角形，OBD也构成等边三角形，所以这个旋转是以60°为旋转角的旋转.

有了以上探寻的成果作基础，我们可以充分利用平移一边不改变角的大小来发现更浅显的证法：

如图5所示，将线段BC平移至线段C'D，发现△C'DE恰为等边三角形.而所求角∠CGE=∠D=60°.

学习数学就要有这种探寻精神，不但善于在生活的现象中发现数学问题，还要能融会贯通地利用初高中的数学知识来解决问题！