基于P-DPC的STATCOM/BESS微电网协同控制策略改进

吴渊军，陈 亮，王亚迪，葛 愿*，王宗跃，陈方静

(1.安徽工程大学 电气工程学院 ，安徽 芜湖 241000；2.安徽省科学技术研究院 项目管理中心，安徽 合肥 230001；3.淮海技师学院 机电工程系， 江苏 宿迁 223800)

分布式微电网技术作为现代电力系统的关键技术之一引起了各国电力行业科研人员的高度重视.静止同步补偿器(STATCOM)在电网中的无功补偿能力和稳定电压的作用使得其在微电网中被广泛应用，但是STATCOM中的电压型逆变器在工作过程中主要是与微电网系统进行无功交换，当系统中存在有功损耗时STATCOM的作用就有所欠缺了.而如果在STATCOM系统中加入蓄电池系统(BESS)，组合成一种既可以对系统进行无功补偿又可以调节有功功率的新装置[1]，即带蓄电池储能系统的静止同步补偿器(简称STATCOM/BESS)，对该装置进行合理的控制能有效地实现电能质量的优化[2].

传统直接功率控制(DPC)是由开关表中预存的电压矢量选择开关状态，并由脉冲生成模块对三相桥臂上的开关管进行通断控制进而实现对功率的调节.传统预测功率下的直接功率控制(P-DPC)可以在没有开关表上电压矢量和开关状态的固定的对应关系下实现开关频率的灵活变化[3]，从而对STATCOM/BESS装置进行控制.但这种多应用于PWM整流器中的控制方法为了简化算法往往是将无功功率置零后再进行控制，而在具有STATCOM/BESS装置的微电网系统中需综合考虑对有功功率和无功功率的控制效果，因此这种控制方法会导致对无功功率控制不足[4]，并且该控制方法采用的线性插值预测参考功率的误差较大.

与传统预测功率下的直接功率控制不同，为了克服无功补偿不足的缺点而将无功功率作为一项控制指标，重新推导了STATCOM交流侧电压的表达式；为了避免线性插值预测参考功率算法引起的误差较大因此采用二阶拉格朗日插值法预测参考功率.仿真结果表明，提出的方法使得STATCOM/BESS系统输出功率波动小、直流侧电压稳定，且具有很好的功率跟踪控制和快速调节功率的能力.

1 STATCOM/BESS的工作原理

STATCOM/BESS系统拓扑结构图如图1所示.图1中STATCOM的直流侧蓄电池与电容并联之后通过电感并联在电网上.因为有了蓄电池的有功调节作用使得STATCOM/BESS系统在运行时能够实现有功无功的双向补偿，也就实现了该系统的四象限补偿能力[5].

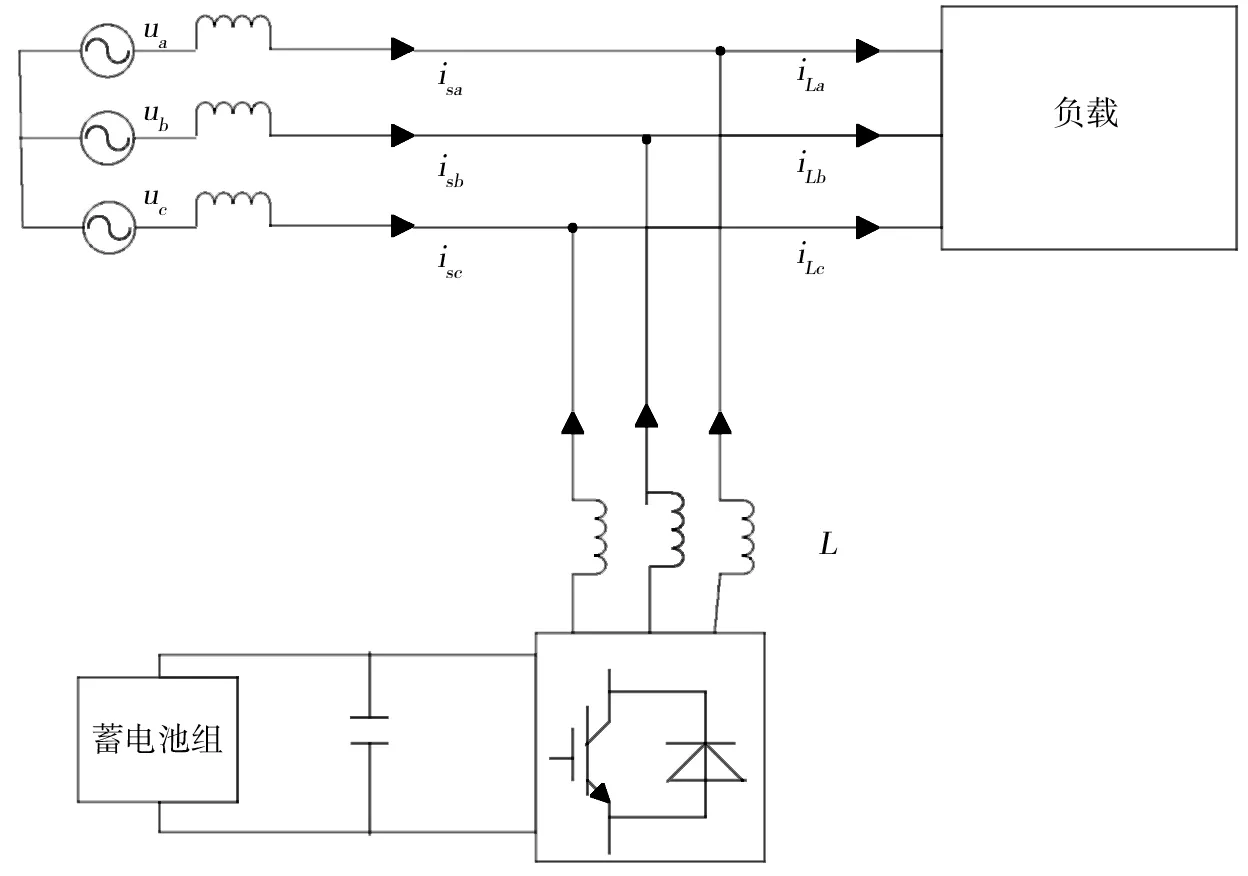
图1 STATCOM/BESS系统拓扑结构图

STATCOM/BESS系统四象限运行模式图如图2所示.图2中E、I分别为STATCOM/BESS装置的输出电压和输出电流相量；V为微电网系统电压相量；X为与装置串联的电抗器；与电抗器X串联的电阻R代表整个线路及装置的有功损耗等效阻值.从图2中可以看出，通过改变STATCOM/BESS装置的输出电压大小和相位即可改变输出的无功功率与有功功率的正负与大小，从而实现电力系统的有功无功双向补偿.

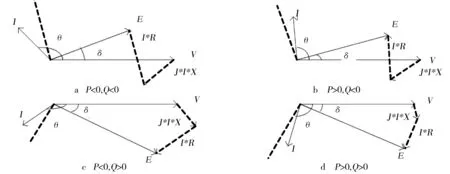
图2 STATCOM/BESS系统四象限运行模式图

2 STATCOM/BESS的数学模型

2.1 STATCOM/BESS电路的简化

STATCOM/BESS控制系统简化的电路图如图3所示.图3中vabc是微电网系统的电压，eabc是STATCOM/BESS的输出电压.将装置中的蓄电池看成一个理想电压源Us与阻值为Rs的电阻串联.STATCOM/BESS装置电路包括三相全桥变流电路、蓄电池组和电抗器，在工作中与微电网并联.由于其本身存在非线性器件而使得数学建模以及控制器设计的难度大大增加[6].STATCOM/BESS数学模型建立的准确性是研究STATCOM/BESS运行特性以及控制器设计的基础，STATCOM/BESS整体装置建立准确的数学模型是STATCOM/BESS装置性能特性分析以及运用正确的控制方法的必要条件[7]，所以建立的数学模型的准确程度将直接影响控制器的设计和系统仿真.

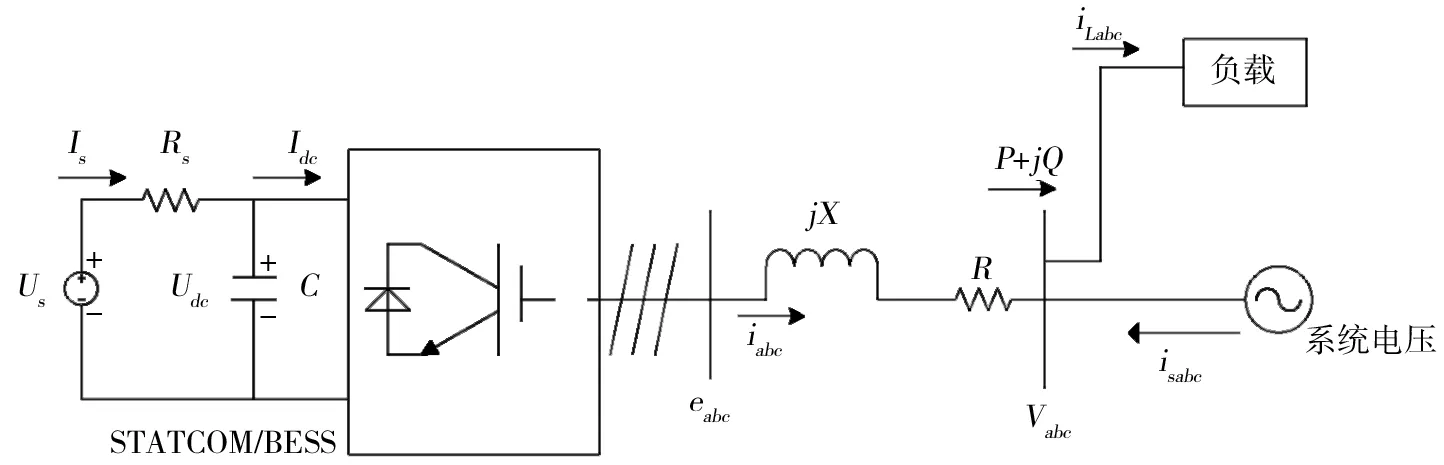
图3 STATCOM/BESS控制系统简化的电路图

为了保证STATCOM/BESS系统数学模型的准确性，需要进行以下3点假设[8]：

①系统中的电压均为三相对称正弦波型电压；

②系统中的电流与电压的谐波不考虑；

③STATCOM中的三相变流电路所使用的开关器件及其他器件均为理想器件，不考虑损耗.

2.2 数学模型的建立[9]

STATCOM/BESS系统中储能蓄电池采用理想电压源Us和电阻Rs串联的模型，建立了集成的控制系统拓扑结构如图3所示.其中vabc是微电网系统的三相线电压系统，也就是低压母线的电压.eabc和iabc分别是STATCOM/BESS装置输出的电压和电流；us为蓄电池最大的断路电压；is为蓄电池的输出电流；Udc是电容的两端电压；Idc是STATCOM/BESS装置的输入电流.R是STATCOM/BESS装置的等效电阻、X是隔离三相变流电路和微电网系统的等效电抗.蓄电池的数学模型采用线性电路模型[10],STATCOM的数学模型采用三相逆变两电平桥式电路模型，通过改变交流输出电压的幅值和相位就能实现STATCOM/BESS装置发出或者吸收满足需要的无功和有功电流，进而实现动态的补偿系统所需的无功功率和有功功率.

由基尔霍夫电压定律，可知：

(1)

对式(1)作park变换，得到：

(2)

并且有

(3)

输入STATCOM/BESS装置的有功功率、无功功率分别为：

(4)

则由式(4)可得：

(5)

由能量守恒可得：

(6)

将式(2)、式(4)代入式(6)得：

(7)

将式(3)、式(7)联立得到STATCOM/BESS装置的状态方程数学模型为：

(8)

式(8)表明：根据数学模型中对控制量的分解与运算，可以通过对补偿电流id、iq的控制来实现对STATCOM交流侧电压的控制.因此，可以通过控制STATCOM交流侧电压在d-q轴上对应电流的大小来实现对STATCOM/BESS输出功率的控制.

3 基于预测功率的STATCOM/BESS直接功率控制改进策略

3.1 改进策略

传统P-DPC控制是由功率预测模型与DPC控制相结合的一种控制策略.将其应用在STATCOM/BESS时，一般是将无功功率置零从而简化控制算法.然而STATCOM/BESS系统的无功功率存在且不容忽略，传统P-DPC控制无法对无功功率进行调节.为了加强对无功功率的控制，重新进行了P-DPC算法的推导，得到STATCOM交流输出电压的新表达式，实现了SVPWM对装置的定频控制.并且采用二阶拉格朗日插值法代替之前的线性插值预测参考功率，不仅简化了算法，还提高了系统的动态响应速度.

3.2 P-DPC改进算法的推导

如图3所示，将微电网电压vabc、交流变流器交流侧电压eabc及电流iabc进行clark变换，得usα、usβ为微电网电压，esα、esβ为交流变流器交流侧电压，iα、iβ为电流.则由瞬时功率理论可知STATCOM/BESS装置的输出有功功率、无功功率分别为：

P=usαiα+usβiβ,Q=-usαiβ+usβiα,

(9)

将式(9)中变量离散化，则得到在k时刻的瞬时功率分别为：

P(k)=usα(k)iα(k)+usβ(k)iβ(k)，Q(k)=-usα(k)iβ(k)+usβ(k)iα(k)，

(10)

由采样理论知：当采样频率远远高于电网电压频率时，可以将电网电压看作是不变的，即:

uα(k+1)=uα(k)，uβ(k+1)=uβ(k)，

(11)

将式(10)、式(11)联立，可得STATCOM/BESS装置输出功率在时刻k到时刻k+1的变化为：

(12)

令采样周期为Ts，则k+1时刻的预测电流为：

(13)

将式(13)代入式(12)得：

(14)

则由式(14)得到STATCOM交流侧电压的矢量esα、esβ：

(15)

式(15)中的P(k+1)、Q(k+1)为实际功率值，但是不能直接得到，只能由预测得到.在实际工程应用时，参考功率Pref及Qref是会随负载改变而变化的变化量，因此是无法准确预测Pref(k+1)、Qref(k+1)的.传统P-DPC控制中所采用的线性插值算法在实际工程应用中负载变化较大会导致产生的误差较大.因此，采用二阶拉格朗日插值法.设有已知3点，其坐标分别为(x0,y0)，(x1,y1)，(x2,y2)，则预测点坐标为:

(16)

则(k+1)时刻的参考功率为:

(17)

为了确保控制的准确度，使得:

(18)

将式(17)、式(18)代入式(15)中，得：

(19)

式(19)中，usα、usβ和iα、iβ可以通过测量得到，采样周期Ts、电阻R和电抗L已知.历史参考功率可以由历史测量的瞬时功率经过计算得到.从式(19)中计算得到的电压矢量esα、esβ可用来直接在固定的频率下通过SVPWM模块实现对三相变流器的开关控制.

3.3 控制系统结构

改进后的P-DPC控制框图如图4所示.由图4可知，P-DPC控制主要包括瞬时功率检测模块、功率预测模块、SVPWM模块.瞬时功率检测模块检测电路中参数并计算出STATCOM/BESS装置输出功率和负载功率，并根据负载功率生成STATCOM/BESS装置参考功率，使STATCOM/BESS发挥抑制功率波动的作用.功率预测模块实现目标矢量esα、esβ的计算，并由SVPWM模块驱动三相桥臂，实现对变流器的跟踪控制.

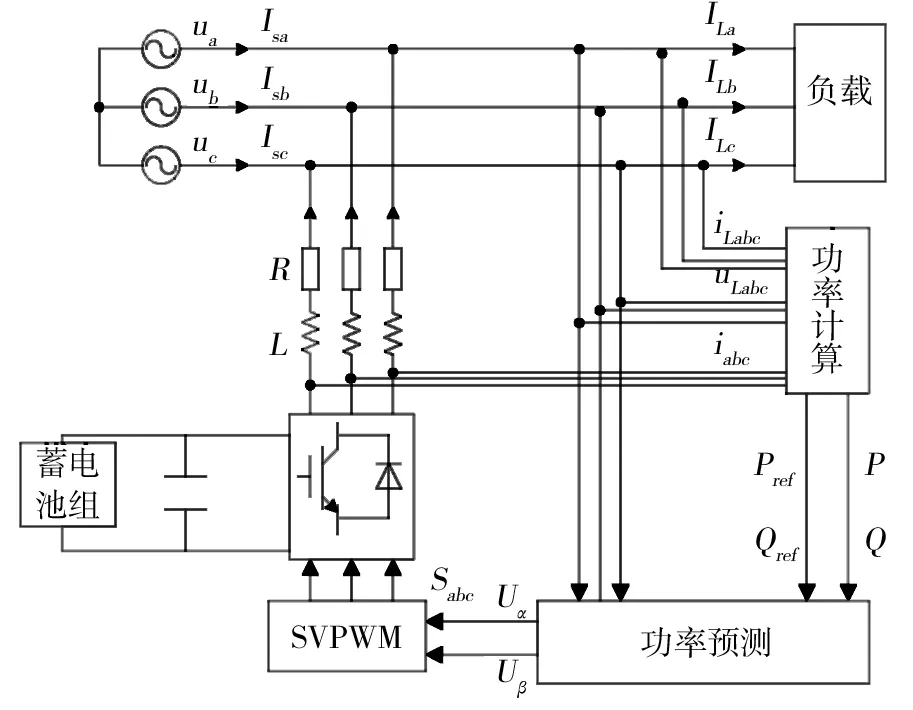
图4 改进后的P-DPC控制框图

4 仿真分析验证

为了验证改进后的P-DPC控制策略有效性，在MATLAB/simulink中建立具有非线性的负载的微电网系统仿真模型.整个系统的等效电路图如图3所示，系统相关参数如表1所示[11].

表1仿真系统参数

参数数值装置容量Q30kvar三相电压源线电压U380V开关频率f5kHz采样时间Ts5*10-6s

4.1 具有感性负载的系统仿真分析

在具有感性负载的微电网系统中进行仿真，负载容量设定为100 kw/60 kvar.为了验证改进后的P-DPC控制的有效性，通过在Simulink中搭建微电网系统模型进行改进前后的控制策略仿真分析，仿真时令STATCOM/BESS装置在0.1 s前不投入运行，在0.1 s时投入使用.由于三相电压中的每相电压只是相位差异，其他特性都相同，所以研究只对A相电进行研究分析，仿真结果如图5所示.在0～0.1 s时，由于没有补偿装置投入系统使用，系统将呈现感性负载特性，如图5a所示，A相电流滞后于电压大约75°.在0.1 s时投入STATCOM/BESS装置后，系统输出的电压和电流波形的相位在改进前后都趋近一致，从图5a、图5b能看出，改进后的电压和电流波形相位基本实现了一致，说明改进后基本实现了无功功率的完全补偿.由图5c、图5d可知，STATCOM/BESS装置在0.1 s投入后很快地发挥了提供无功功率的作用，改进后的系统在投入0.02 s之后就能保持稳定的无功功率输出，比改进前响应更快.

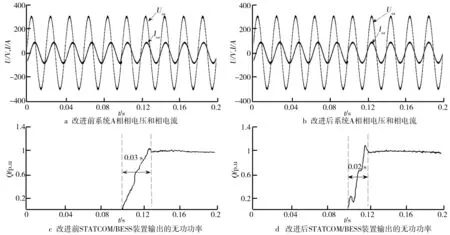
图5 在具有感性负载的微电网系统中仿真结果

4.2 系统中感性负载突变为容性负载仿真分析

在始终有STATCOM/BESS装置工作的系统中，在0～0.1 s时接入100 kw/60 kvar的感性负载，在0.1 s时突变为60 kw/100 kvar的容性负载.这样的系统仿真结果如图6所示.如图6a、图6b所示，微电网系统中的负载类型在0.1 s时发生突变，但是系统电流基本保持不变，是由于STATCOM/BESS装置的无功调节.在图6a中，在0.1 s前电流波形比电压波形滞后一些，而在0.1 s之后电流波形又超前于电压波形，这是由于微电网系统中的负载类型在0.1 s时从感性负载突变成容性负载.在图6b中，改进后的控制策略使得系统的电压波形与电流波形基本实现了相位一致，比改进前具有更好的功率调节能力.从图6c、图6d可以看出，STATCOM/BESS装置在系统中负载类型发生突变时进行了无功功率补偿或者吸收，并且改进后的调节时间更短，说明改进后的装置更具有快速功率调节的作用.

图6 微电网系统中感性负载突变为容性负载仿真结果

5 结论

对STATCOM/BESS系统装置中将功率预测和直接功率控制相结合的P-DPC控制的改进算法进行研究.针对传统的P-DPC控制对无功功率控制不足，且控制响应速度慢导致功率跟踪不足等问题，在描述STATCOM/BESS系统装置的工作原理、推导数学模型后,提出对传统P-DPC控制的改进方案.即在考虑无功功率下重新推导了P-DPC控制算法，并采用了算法更简单、控制精度更高的拉格朗日插值法代替传统的线性插值法.最后，通过仿真说明改进后的算法可以使微电网系统中STATCOM/BESS装置在保证直流侧电压稳定的前提下，能够快速调节功率且具有很好的功率跟踪控制.