团数的DNA折纸术计算模型

崔建中,殷志祥,杨 静

(1．安徽理工大学 电气与信息工程学院, 安徽 淮南 232001；2．淮南联合大学 计算机系， 安徽 淮南 232038；3．安徽理工大学 数学与大数据学院, 安徽 淮南 232001)

DNA折纸术[1]是近年来提出的一种新的DNA自组装方法，是目前DNA自组装领域研究的热点问题.与DNA模块自组装相比，DNA折纸术能构造出更复杂、精细的纳米结构，且DNA链的设计简单，组装效率较高.它的原理是利用较短的DNA订书钉链(Staple)，按碱基配互补对原则，对一条较长的脚手架链(Scaffold)进行折叠，从而构造出理想的纳米结构.文献[2]利用DNA 折纸术原理成功地构造出纳米中国地图，证明了DNA折纸术具备构造非对称图案的能力.文献[3]将文献[1]的方法加以推广，并成功地构造出方螺帽等6种三维结构.文献[4]利用折纸术折叠成长方形的纳米结构来编码有向图的顶点，给出了通过该长方形结构的自组装寻找最短哈密顿路的方法.文献[5]采用DNA 纳米折纸结构编码无向图的顶点，借助纳米结构之间的粘性末端进行自组装，给出了图着色问题的一种解决方法.文献[6] 利用方形DNA折纸作为基本单元，以递归方式进行多次自组装，得到了微米级蒙娜丽莎的图案.文献[7]设计了三维砖形DNA基本折纸单元，可以组装成更大尺寸的三维结构.文献[8]利用V形DNA折纸作为基本单元，通过控制基本单元之间的几何形状和作用，可以构造更大的组装体.文献[9]提出了利用噬菌体制备DNA折纸所需的DNA链，为DNA折纸的应用和量产提供了保障.

最大团问题(Maximum Clique Problem)是图论中经典的组合优化问题，也是一类NP完全问题.最大团问题在计算机视觉、市场分析、编码理论中都有非常广泛的应用.文献[10] 使用双链DNA分子编码无向图的顶点，建立初始数据池，根据补图中相邻的顶点不可能同时出现在极大团中，在初始数据池中并行地删除非解.最后，初始数据池中长度最短的DNA分子编码的顶点即为所求的最大团.文献[11]给出了利用质粒求解最大团问题的算法.文献[12]将剪枝策略运用到DNA计算中，给出了基于粘贴模型的最大团问题的算法.文献[13]给出了基于环形DNA分子求解最大团问题的计算模型.文献[14]提出了最大团问题的Tile自组装模型.

图G中最大团的阶数即团数，记为ω(G)，它与图的色数x(G)密切相关.易知，若图的团数为K，则该图至少是K-着色的.目前，DNA折纸术主要应用在纳米技术领域.将DNA折纸术应用于搜索简单无向图的最大团，进而求解图的团数.该模型利用订书钉链折叠脚手架链形成发夹结构，凝胶电泳检测发夹结构的变化来建立初始数据池、删除非解、读解.该模型简单、读解方便、可行性高.文中提出的计算模型一方面证明了DNA折纸术可以用来求解组合优化问题，另一方面也证明了订书钉链与脚手架链的杂交，结合链置换，凝胶电泳从算法的角度是完备的.它不仅拓宽了DNA折纸术的应用领域，也为解决组合优化问题提供了一种新的思路和方法.

1 团数问题

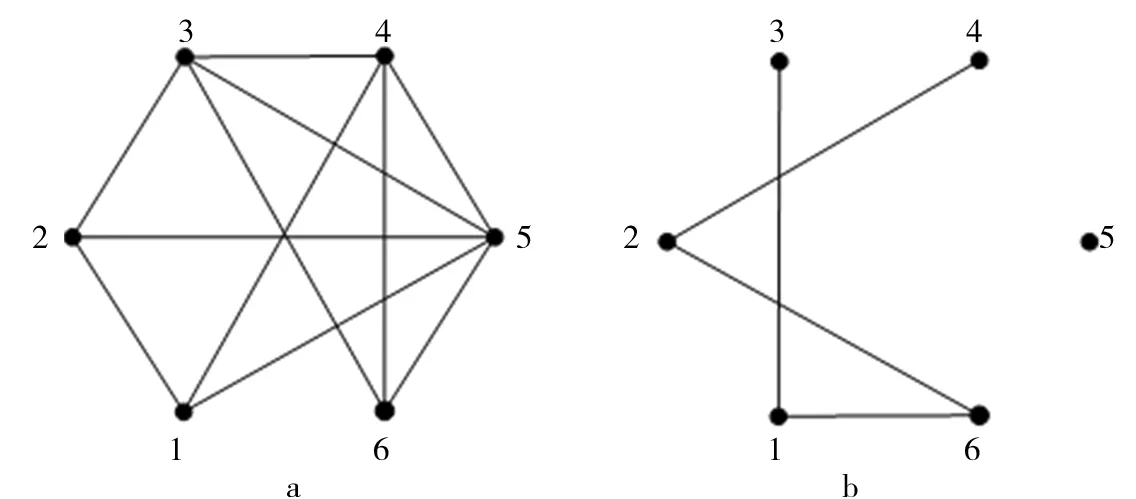
图1 简单无向图及其补图

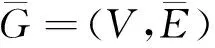
2 团数问题的DNA折纸术计算模型

2.1 脚手架链和订书钉链的设计

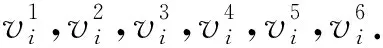
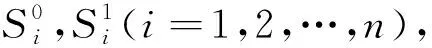
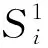
2.2 团的表示

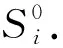
图2 脚手架链(中)与订书钉链上(下) 图3 团的表示

按照这种方法，最大团{3,4,5,6}的示意图如图4所示.

图4 最大团

2.3 算法

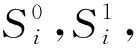
步骤1：

Fori=1 ton

Divide(T0→T1,T2)

Merge(T1,T2→T0)

Gel(T0)=l+ny→T0

Endfor

步骤2：

Fori=1 tom

Forj=i+1 tom

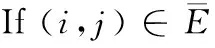
Divide(T0→T1,T2,T3)

Merge(T1,T2,T3→T0)

Endif

Gel(T0)=l+ny→T0

Endfor

Endfor

步骤3：

Gel(T0)=lmin→T0

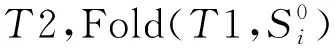
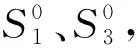
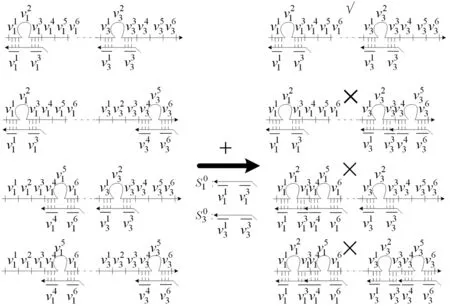
图5 再次折叠脚手架链选择编码正确的团

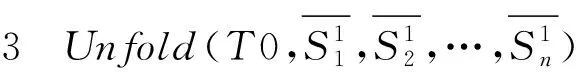
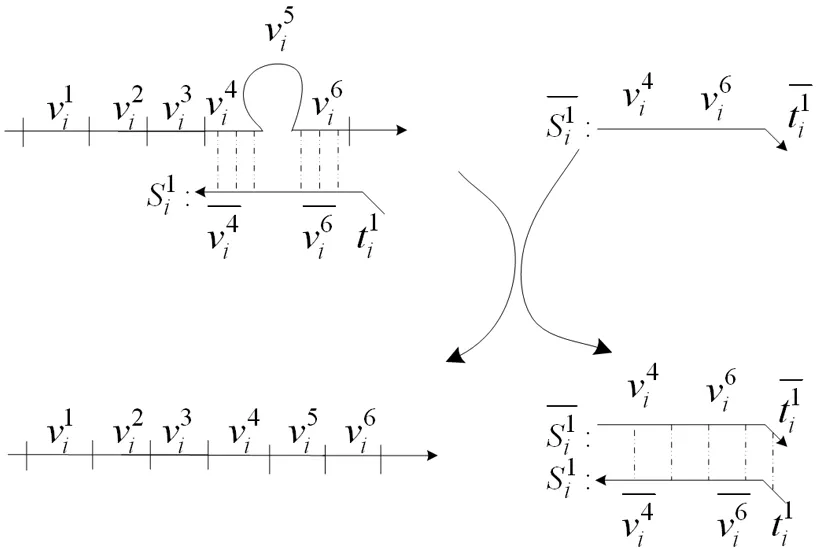
图6 链置换打开表示顶点i在团中的发夹结构

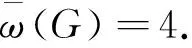
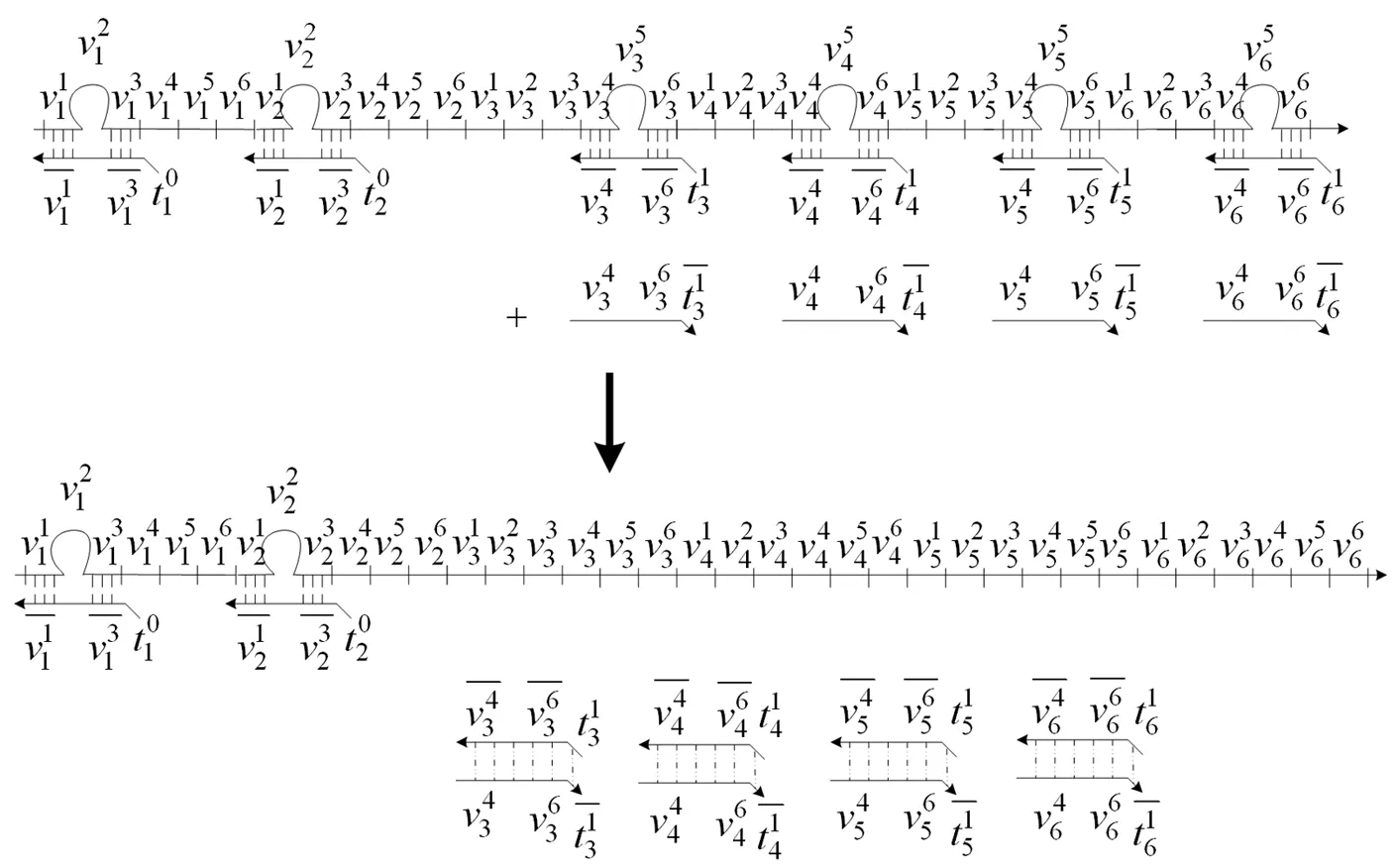
图7 打开表示顶点在团中的发夹结构的示意图

2.4 算法复杂度

对于简单无向G(V,E)，其中|V|=n,|E|=m，文中提出的计算模型需要编码n种寡聚核苷酸片断表示给定图中的顶点，将这n种寡聚核苷酸片断连接构成脚手架链.当表示顶点的寡聚核苷酸片断编码完毕，相应的订书钉链及钉书钉链的补链的编码也随之确定.因此，文中提出的模型的编码复杂度为O(n).

在初始数据池中，为表示所有可能的团，模型需要n次折叠脚手架链，1次凝胶电泳，生成脚手架链上发夹结构的组合.然后，针对补图中的每条边，需要3次折叠脚手架链，1次凝胶电泳，删除非团.因此，共需3m次折叠脚手架链，m次凝胶电泳.最后为确定团数，需要1次打开脚手架链上的发夹结构，1次凝胶电泳.故模型的时间复杂度为O(n2).

与其它的DNA计算模型相比，文中提出的计算模型初始数据池中仅含有一种类型脚手架链，与问题的规模无关，脚手架链上发夹结构的组合为2n，它对应编码的顶点是否在团中的所有可能情况.脚手架链上发夹结构的变化可通过脚手架链的长度反映出来，凝胶电泳可以准确、可靠地判断发夹结构的变化，故模型的可靠性大大增加，可行性更高.

3 结论

应用DNA 折纸术求解团数问题，提出了团数的DNA折纸术计算模型.其核心思想是利用DNA折纸术，结合链置换，将团数映射为脚手架链上表示顶点在团中的发夹结构的数目，通过凝胶电泳检测脚手架链的长度，进而判断发夹结构的变化.DNA 折纸术的最大优点在于DNA链的编码简单，脚手架链和订书钉链杂交反应的相对浓度要求不高，实验简单，组装效率高.将DNA折纸术的核心思想应用于组合优化问题的求解，结合凝胶电泳判断发夹结构的变化，读解更简单，从而提高了DNA计算模型的可行性、可靠性.文中提出的模型目前仅能求出给定无向图的团数，而最终确定最大团中的顶点仍需要结合其他的读解方法，如分子信标，这也是下一步要进行的工作.文章从理论层面证明了订书钉链与脚手架链的杂交，结合链置换，凝胶电泳从算法的角度是完备的.它不仅扩宽了DNA折纸术的应用领域，也为解决组合优化问题提供了一种新的思路和方法.