基于船体三自由度井喷液柱高度测量方法*

刘书杰，耿亚楠，任美鹏，胡乔波，孙晓峰

(1.中海油研究总院有限责任公司，北京 100012；2.东北石油大学 高效钻井破岩技术国家工程研究室，黑龙江 大庆 163318)

0 引言

海洋石油资源[1]储量丰富，占全球石油资源总量的34%。随着海上油气勘探开发技术的发展，海洋油气产量稳步上升，已成为世界油气产量新的增长点。在海洋油气资源钻井过程中，由于地层压力掌握不准确、泥浆密度偏低、井内泥浆液位降低或起钻抽吸等原因，可导致钻井液压力小于地层油气压力，地层油气迅速侵入井筒，演变成不可控的井喷事故[2-3]。对于海洋钻井来说井喷失控是灾难性事故，由于远离陆地，很难迅速救援，井喷失控往往造成难以估计的经济和生态损失，如2010年墨西哥湾的深水地平线钻井平台井喷[4-5]爆炸沉没，历经83 d救援，泄漏的原油造成了墨西哥湾沿岸巨大的生态灾难。

海上钻井平台发生井喷事故后，需要第一时间获得井喷参数，如井口喷流压力、喷流流体性质等、根据井喷参数预测地层压力，制定压井方案。但当井喷失控后，为保障员工人身安全，需要工作人员立刻撤离海洋钻井平台，无法直接读取井口压力参数，此时平台井口井喷液柱高度是反应井口压力的可靠参数，可以依据井喷液柱高度计算井口压力[6]。井喷失控后，井喷液柱高度已经不能在平台上直接测量，通过救援船远程测量井喷液柱高度就成为可行的方法，但国内外文献中对这类测量方法却鲜有提及。目前，对于远程物体高度测量研究较多，一般有以下几种方法：刘劲彪、Teh等[7-8]提出激光电测法测量海上波浪高度；Bolanakis等[9]采用气压测量法测量物体海拔高度；Chulichkov、蒋李兵等[10-11]设计的图片像素法亦可以精确测量建筑物高度。上述测量方法中测量点是稳定的固定点，而救援船测量点受海洋环境影响是非稳定的测量点。

上述几种方法用于海上井喷高度测量弊端明显，一则器材昂贵不利于存放运输；再者受天气和环境干扰误差大，不符合现场实际应用。为解决恶劣环境下远距离井喷液柱高度测量问题，本文提出1种基于船体三自由度井喷液柱高度测量方法。该方法将难以直接测量的液柱高度转化为三倾角测量，应用三角函数变换，计算井喷液柱高度，然后对测量值进行卡尔曼滤波[12-13]处理，进一步提高测量精度。该方法克服了其他测量方法受环境影响大、误差严重的问题，

1 井喷液柱高度测量设备及测量方法

将难以直接测量的井喷液柱高度转化为三倾角测量，倾角测量将采用自设计的倾角测量装置，其结构如图1所示。这种倾角测量装置由望远镜、结构支架、镜片组、活动臂、角度测量传感器组成。镜片组包括高点观测镜、动镜及固定镜，其中，固定镜为半透明半反射的平面镜，动镜为凸透镜；高点观测镜与活动臂一端相连，置于结构支架顶端，可在1/6圆周内自由旋转；角度测量传感器镶嵌在活动臂上；固定镜与小型望远镜处于同一水平高度，全部组件按如图1所示的位置排列。

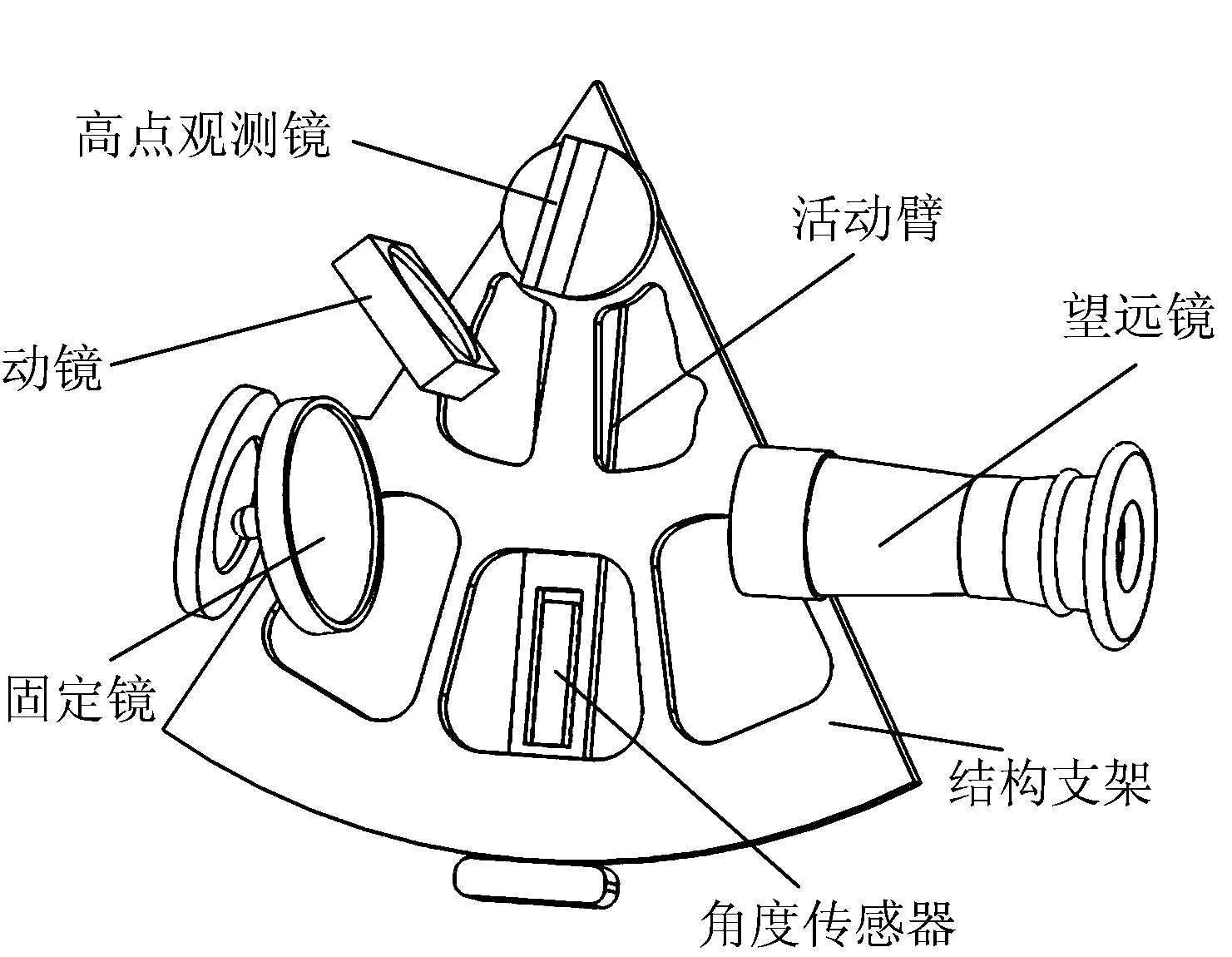
图1 倾角测量装置结构示意Fig.1 Schematic diagram of the inclination measuring device

倾角测量装置正常工作时，望远镜水平放置，对准井喷流体液柱，调节活动臂使高点观测镜对准井喷流体高点位置，转动固定镜使光线水平传入望远镜，记录角度传感器读数。倾角测量装置角度测量原理如图2所示。

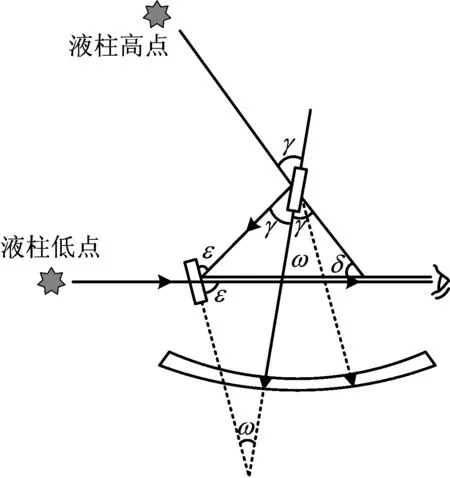
图2 角度测量仪器测量原理示意Fig.2 Angle measuring instrument measurement schematic

图2中，δ为液柱实际倾角，(°)；ω为角度传感器示数。根据三角函数关系，在△DEG中存在角度变化规律为：

γ+(180°-ε)+ω=180°

(1)

同理，在三角形△ABO中亦存在以下角度关系：

2γ+(180°-2ε)+δ=180°

(2)

联立式(1)与式(2)，求得：

δ=2ω

(3)

即测量示数为实际角度的一半，后文中，式(1)～(3)应代入实际角度参与计算。

2 船体处于平静海面时的井喷液柱高度测量

假定观测船航行在无限深广的静水中，船体为刚体，无浪无海流作用，船体平稳航行。角度测量装置置于甲板上，甲板平面平行于海平面。通过处于同一直线上3个角度传感器进行倾角测量，得到3测点A，B，C测量角度分别为α1，α2，α3。如图3所示。

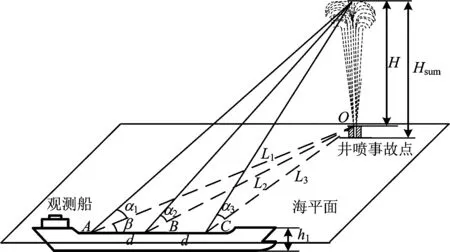
图3 高度测量方法示意Fig.3 Height measurement method diagram

如图3所示，设甲板高度为h1，m；吃水深度为h2，m。传感器距甲板高度为h3，m；两角度传感器间距为d，m。根据三角函数相关定理，求得观测点距井喷液柱平面距离分别为：

(4)

式中：L1，L2，L3分为A，B，C这3个观测点距事故井水平投影距离，m；H为传感器距井喷液柱最高点垂直距离，m；α1，α2，α3，分别为3个观测点测量角度，(°)。

分别在三角形△ABO与△ACO中分别应用余弦定理可得：

(5)

(6)

式中：β为水平投影面中L1与传感器连线所在直线夹角，(°)；d为两角度传感器间距,m。

联立式(5)与式(6)，得到三水平投影距离关系式为：

(7)

将式(4)中表达式代入式(7)中得到高度H的表达式为：

(8)

综上，井喷液柱总高度Hsum为：

(9)

3 船体处于波动海面时的井喷液柱高度测量

观测船在航行过程中，受风浪流载荷作用，船体会发生摇晃倾斜，对这种运动状态可以简化描述为三自由度[14]运动，即横摇，纵倾和垂荡，如图4所示。

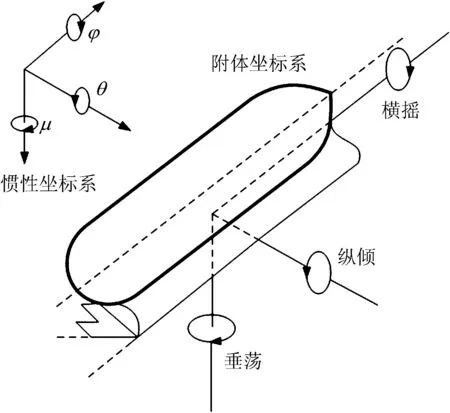
图4 船体三自由度示意Fig.4 Schematic three-degree of freedom diagram

船体发生摇晃后，甲板平面(测量传感器平面)与海平面不再平行，产生倾角，对高度测量计算造成影响。分别考虑3种倾斜状态给出修正后的高度计算公式。

第1种情况，仅考虑横摇状态对井喷液柱高度测量的影响。设横摇倾角为φ，(°)。发生横摇时，实际倾角为角度测量传感器所测角度与横摇倾角之差，即：

α实=αn-φ(n=1,2,3)

(10)

将实际角度表达式(10)代入式(9)中，得到横摇时井喷液柱修正高度H修1为：

H修1=(h-h1)+h2+

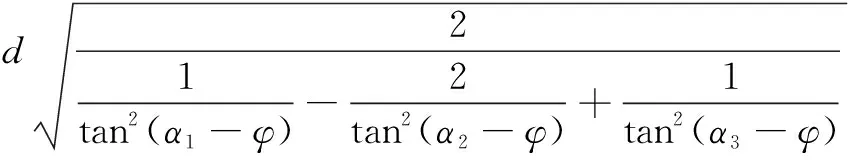
(11)

第2种情况，仅考虑纵倾状态对井喷液柱高度测量的影响。设纵倾倾角为θ，(°)。每个角度测量传感器不处于同一水平高度，导致传感器到井喷液柱最高点垂直距离出现差别，充分考虑纵倾状态对液柱高度测量的影响，得到修正后的计算公式为：

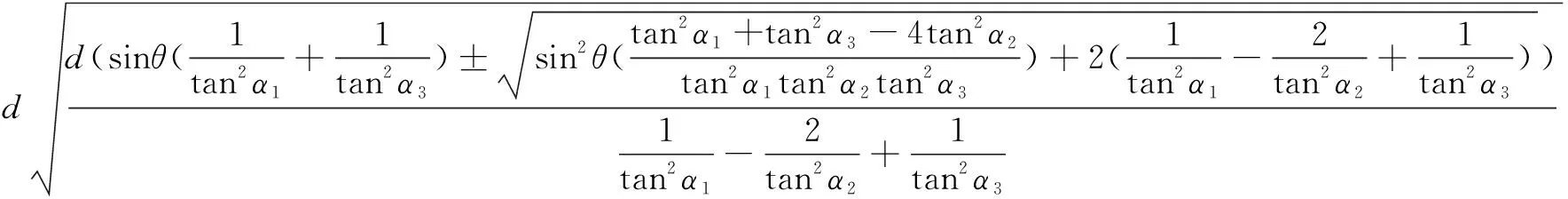
(12)

第3种情况，仅考虑垂荡状态对井喷液柱高度测量的影响，设垂荡高度为μ，m。船体处于垂荡状态仅改变传感器到井喷液柱最高点垂直距离，只需要在式(9)中增加垂荡高度相即可，得到修正后的高度计算公式为：

(13)

综合考虑以上3种因素，即横摇、纵倾和垂荡对井喷液柱高度测量的影响，得到修正后的高度计算公式为：

H修=(h-h1)+h2+

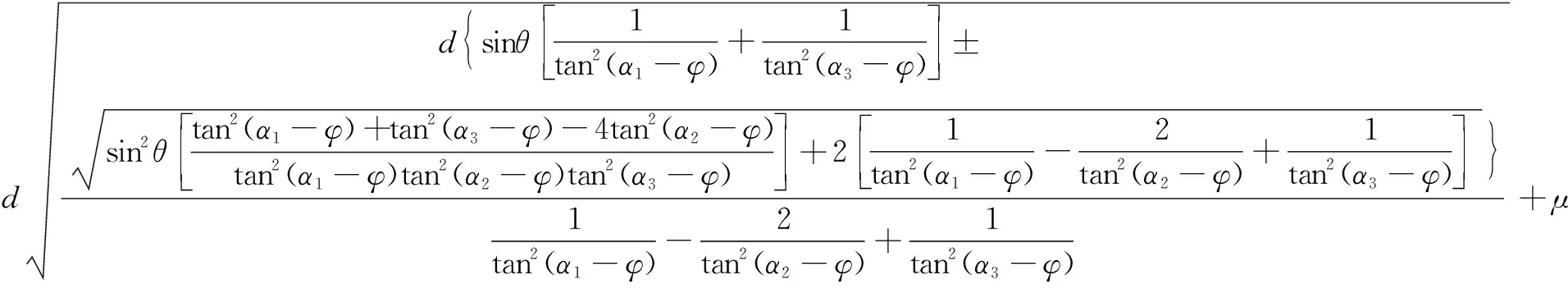
(14)

4 井喷液柱高度测量精度分析及改进

本研究中应用角度测量传感器对井喷液柱高度进行测量，影响高度测量精度的因素有以下几个方面：传感器测量精度、甲板振动和传感器布置位置。

首先分析传感器自身测量精度误差的影响。根据现场实际需要，假设观测船距井喷事故井400 m，井喷液柱高度大约40 m，要求井喷液柱高度测量误差小于5%(即测量结果误差小于2 m)。通过式(9)运算分析，对应角度误差小于0.57°。因此，选择光栅式角度传感器[15]，光栅式传感器依据莫尔条纹现象，测量精度可达0.06°，测量输出信号易数字化处理，可进行动态监测。

在现场实际操作过程中，角度传感器不可避免地受甲板振动的影响，造成测量结果波动严重，影响测量精度。应采用滤波算法进行信号处理，提高测量精度。振动杂波信号一般为高斯白噪声，使用卡尔曼滤波方法对收集信号进行滤波处理。

离散卡尔曼滤波算法的相关公式如下：

1)系统方程

Xk=ΦXk-1+HWk

(15)

2)测量方程

Zk=CXk+Vk

(16)

式中：C=[1,0]；Zk为测量输出；Vk为测量噪声。

Vk与Wk不相关，同时还要满足方程E[Vk]=0；E[Vk,VjT]=Rδkj；E[Wk]=0；E[Wk,WjT]=Qδkj。其中，Q为系统方差阵，R为测量方差阵。

3)1步预测阵

(17)

4)状态估计

(18)

5)增益

Kk=Pk/(k-1)CT(CPk/(k-1)CT+R)-1

(19)

6)1步预测方差估计

Pk/(k-1)=ΦPk-1ΦT+HQHT

(20)

7)方差估计

Pk=(1-KkC)Pk(k-1)

(21)

在实际操作中，传感器位置对测量结果有很大的影响，假设井喷液柱高度为40 m，观测船距事故井口400 m，分析传感器间距对测量精度的影响。为简化计算令式(9)中α1=α3，计算结果如图5所示。

图5 测点距离与传感器角度差关系Fig.5 Measuring point distance and sensor angle difference curve

从图5中可知，随测点间距的增加，两传感器测量值差值越大，差值越大分辨率越高，测量精度也就越高。换言之测点间距越大，测量结果越精准。为满足仪器精度(0.01°)的要求，最小间距应大于24 m，最大间距受船只尺寸限制，原则上距离越大，测量越精准。

5 实验验证

为了验证角度计算公式合理性与测量方法的准确性，设计模拟实验。分别针对水平、横摇、纵倾、垂荡以及多因素耦合作用情况进行分析验证。

实验参数设置如图6所示，观测场地为20 m×20 m方形场地，目标高度H=5.00 m，测点间距为d=5.00 m，测点连线与正西方向夹角为ρ=30°。

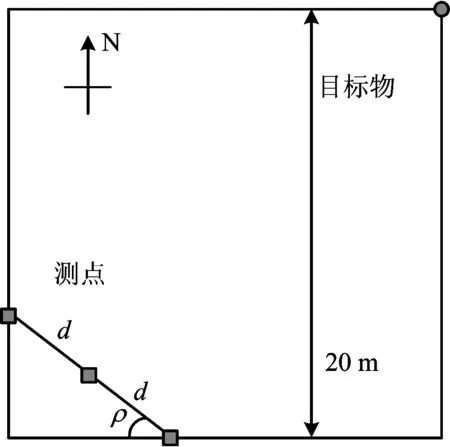
图6 实验布置示意Fig.6 Experimental layout

横摇角度为2°，纵倾角度为2°，垂荡高度为0.2 m，得到实验结果如表1所示。

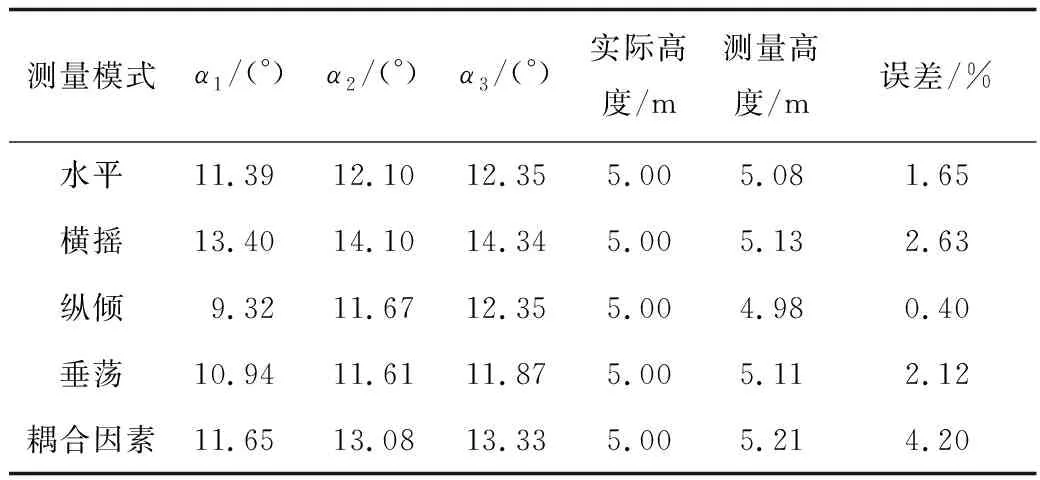
表1 实验结果统计Table 1 Statistics of experimental results

分析表1可知，在考虑三自由度对高度测量的影响的前提下，实验最大误差为4.2%，满足现场实际要求，本方法可以用于井喷液柱高度测量。

6 结论

1)为满足井喷液柱高度测量配套测试方法使用，研究提出了一种新型倾角测量装置，经实验验证，可以满足角度测量要求。

2)高度测量精度受倾角传感器测量精度影响大，可通过调节测点间距将其消除。在测量精度为0.01°，距离为400 m时，为保证测量精度两测点间距应大于24 m，同时测点间距越大，测量精度越高。

3)数据信号处理采用卡尔曼滤波法，较好地消除了甲板震动等因素的影响，可有效地提高测量稳定性与准确性。

4)模拟实验验证中，针对高度为5 m的目标物体，不同船体状态下的测量结果误差均控制在0.21 m以内，误差小于4.2%，能够满足海洋井喷救援测量应用需求。