岩爆相似材料的最优配比试验研究*
2018-11-30侯廷凯周宗红余洋先王大明靳西传
侯廷凯,周宗红,余洋先,王大明,靳西传
(1.昆明理工大学 西部优势矿产资源高效利用教育部工程研究中心,云南 昆明 650093;2.四川二八二核地质工程有限公司;四川 德阳 618000)
0 引言
相似材料是按一定的相似关系,将与原型力学性质相似的原料通过特定比例制成缩尺模型的统称,通过对相似材料进行模拟试验可以研究理论分析与数值模拟较难解决的复杂问题[1]。
在实际深部开挖研究中,因局限于工作环境,岩石取芯难度大;对于成功取得的岩芯,室内力学参数由于岩石的各向异性通常表现出较大的离散性,不能代表岩石的整体力学特征[2],因此,制备深部岩石相似材料进而对其开展相关力学特性的研究具有十分重要的理论和现实意义。相似模拟试验中最重要的是模型试件能否真正体现原材料的特性,这关系到试验能否顺利进行,也关系到模拟试验结果的准确性,其关键在于找到合适的原材料以及各原材料之间的配比。
对于岩石相似材料的制备,前人做了大量的研究。其中,王永岩等[3]以砂子为骨料,石蜡为胶结剂,石膏为调节剂,相似地制成了一批可以模拟页岩的模型试件;申艳军、耿晓阳等[4-5]制备了类砂岩的相似、材料并对其进行物理相似模拟;王雅雯等[6]以石英砂、重晶石粉、铁精粉和松香酒精溶液为原料,制作了铁精砂的相似材料,研究了各成分对试件力学性质的影响,最终得出各材料的最优配比;任大瑞等[7]以石膏、石英砂制成相似材料试件,研究了在不同尺寸、温度、含水率及加载速度下,试件单轴抗压强度及弹性模量的变化规律。
目前大多数的研究是关于软、硬岩相似材料,也包括多种工程模拟对象,但是将白云岩作为相似模拟对象并结合特定工程背景进行研究的试验还比较少,白云岩作为云南某矿山的主要围岩,近年来,随着开采深度加大,岩爆时有发生[8]。对此,本文结合前人的研究成果,以云南某矿山深部白云岩为研究对象,通过对试验数据的方差和极差分析,研究相似模拟试件的力学特性;对试验数据进行拟合得到多元线性回归公式,结合相似理论得出白云岩相似试件最优配比,且回归公式可作为后续白云岩制备的经验公式。
1 相似材料的选择和制备
1.1 相似材料的选择
相似材料的力学特性很大程度上取决于胶凝材料,物理特性很大程度上取决于骨料的材质[9]。在大量参阅前人设计方案的基础上,选用砂、水泥、石膏、硼砂和减水剂作原料,其中骨料选用标准砂,胶凝材料选用石膏和水泥。水泥硬化后强度较高但脆性不明显,石膏硬化后具有显著的脆性特征,但表观密度小、强度低,水泥和石膏的结合可以有效克服自身的缺点,使混合物具有良好的可塑性,故用42.5型早强型硅酸盐水泥和高强石膏粉混合作胶凝材料,按不同配比制成相似材料模拟试件,且在原材料内加入缓凝剂和减水剂[10]。加入减水剂可以减少原料中自由水的数量,避免试件因自由水蒸发而产生裂隙;加入缓凝剂可以延长水与原料作用的时间,为将混合物放入磨具留下充足的时间。
1.2 相似材料的制备
采用圆形双开钢模具制备2种尺寸分别为Φ50 mm×100 mm,Φ50 mm×50 mm的圆柱形试件,根据制作规程要求两端面偏差允许范围为±0.05 mm,垂直度偏差允许的范围为0.25°。
2 正交试样方案的设计及参数测试
当因子个数较多且需要安排多次试验时,正交设计是较常用的1种设计方法,可以巧妙地安排试验,在达到同等统计效果的前提下,减少试验次数,缩短试验周期。
2.1 相似材料正交设计方案
本试验基于正交设计方案,设计4个影响因素,分别为因素A:石膏水泥比、因素B:掺砂率、因素C:掺水率和因素D:硼砂含量,对每个影响因素设定4个水平。4种影响因子的水平见表1,安排16次试验,每次试验制备3个试件。正交设计表选用L16(45),如表2所示。

表1 4种影响因子的水平值Table 1 Level values of four influencing factors
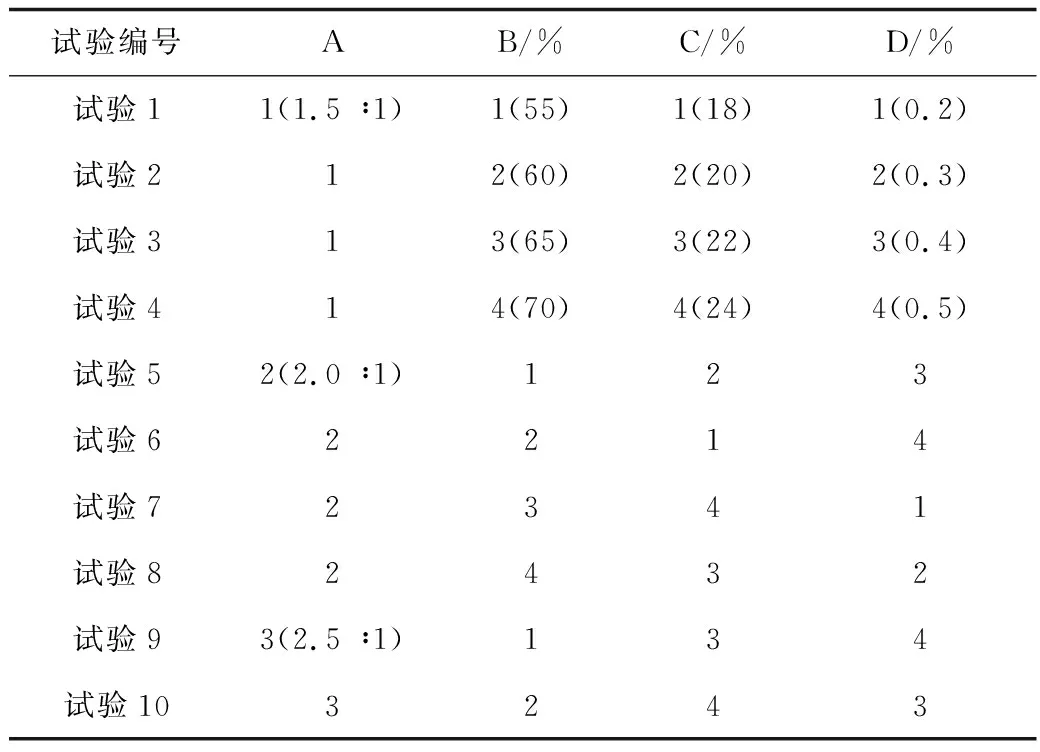
表2 正交试验设计方案Table 2 Orthogonal design experiment scheme

表2(续)
2.2 相似材料力学测试
将不同配比的相似模拟试件进行单轴压缩和巴西劈裂试验。如图1所示,将试件放入压力机内,均以0.5 MPa/s的负荷加载至试件破坏,自动记录主应力σ和变形数据ε。通过对16组不同配比的相似试件进行试验得到其单轴抗压强度σc、抗拉强度σt、抗压抗拉比σc/σt以及弹性模量E的结果(见表3)。

图1 单轴压缩和劈裂试验Fig.1 Uniaxial compression and splitting test chart
由表3可知,相似材料的单轴抗压强度分布在4.580~19.108 MPa之间,抗拉强度分布在1.004~3.423 MPa之间,弹性模量分布在0.792~3.554 GPa之间,力学参数的分布范围较广,可以满足相似材料模型试验的要求。
3 正交试验结果分析
极差分析和方差分析是正交试验设计中最常用的分析方法,本文用2种分析方法并结合主效应贡献图来对各影响因素进行敏感性分析。
3.1 相似材料影响因素敏感性极差分析
极差分析即为每个因子平均值的最大值减去最小值,极差大反映了影响因素对研究指标影响比较明显,反之不明显。极差分析可以简单直接的反映数据间的离散度:
X=Xmax-Xmin
(1)

表3 相似模拟材料的正交试验结果Table 3 Orthogonal test results of similar simulated materials
式中:Xmax为因子平均值的最大值;Xmin为因子平均值的最小值。
结合表2和表3,以因素B在水平2下对单轴抗压强度的影响为例,涉及到试验2,6,10,14的抗压强度值,其平均值为:
(14.347+4.580+10.162+6.978)/4=9.017
同上,各影响因素在不同水平下对单轴抗压强度影响的均值和极差分析如表4和图2(a)所示。

表4 单轴抗压强度的极差分析Table 4 Range analysis of σc
由表4可知,因素B对相似材料单轴抗压强度的极差最大,达到8.606,说明因素B对σc的影响最明显,起主导作用,通过极差排序,各因素对单轴抗压强度的影响程度为B>A≈D>C,即随着石膏水泥比(因素A)和掺砂率(因素B)的增大,单轴抗压强度呈现出逐级降低的趋势,其他2个影响因素对单轴抗压强度的影响不是十分明显。

图2 各影响因素对研究指标的贡献效应Fig.2 The contribution effect diagram of each influencing factor to the research index
为避免重复,图2仅列出了各因素对单轴抗压强度、抗拉强度、抗压抗拉比、弹性模量影响的极差分析主效应。由图2可知,各因素对抗拉强度的影响程度大小依次为B>D>A>C,随着掺砂率(因素B)和掺水率(因素C)的增大,抗拉强度呈现出逐渐降低的趋势,随着硼砂含量(因素D)的增加,抗拉强度先增大后急速下降,石膏水泥比(因素A)对单轴抗压强度的影响无具体规律可循,说明控制相似试件的抗拉强度σt,掺砂率(因素B)起主要作用;各因素对抗压抗拉比的影响程度大小依次为B>A>C>D,随着掺水率(因素C)的增大,抗压抗拉比呈现出逐渐升高的趋势,石膏水泥比(因素A)和掺砂率(因素B)对抗压抗拉比的影响无明显关系;各影响因素对弹性模量的影响程度大小依次为D>C>B>A,弹性模量随着石膏水泥比(因素A)的增大逐渐下降,随着硼砂含量(因素D)的增加逐渐增加。
3.2 相似材料影响因素敏感性方差分析
方差分析是通过对分组试验数据进行分析,检验在一定假设条件下各组均值是否相等,由此判断各因素对研究指标的影响是否显著。根据Fisher相关理论[11],在给定显著性水平α=0.10下对因素A,B,C,D提出统计假设:
H0A:α1=α2=α3=α4=0;H0B:β1=β2=β3=β4=0
H0C:δ1=δ2=δ3=δ4=0;H0D:σ1=σ2=σ3=σ4=0
其中,α,β,δ,σ分别表示因子A,B,C,D在第j个水平下的效应。全体样本试验结果总和如公式(2)所示:
(2)
式中:Kjl为第j列第l水平的数据之和。令:
(3)
式中:n为总的实验次数;m为第j列下水平j出现的次数。
因子的方差平方和为该因子所在列相应的S2j;离差平方和为空列对应的S2j之和。
(4)
式中:S2A为因子的方差,S2A=S2j;S2E为误差平方和,S2E=S24;R为因子的水平数。
以抗压抗拉比的敏感性分析为例,具体计算分析因素A对σc/σt影响的显著性,由式(2)~(4)可以计算得:
(5)
查表得当显著性水平为0.10时F0.90(3,3)=5.39,2.479<5.39,故接受原假设,认为因素A对抗压抗拉比的影响不显著。
按上述方法分别对影响研究指标的各因素进行方差分析,详细过程不再赘述,计算结果见表5。

表5 各影响因素的方差分析Table 5 Variance analysis of various influencing factors
由表5可知,掺砂率对试件单轴抗压强度和抗拉强度影响较为显著,同极差分析结果一致。
各影响因素对抗压抗拉比弹性模量的影响均不显著。相较于4个影响因素,掺砂率对抗压抗拉比的影响最大;硼砂含量对弹性模量的影响最大。
4 相似材料力学参数的拟合与最优配比的确定
4.1 相似材料力学参数的拟合
参照表3的试验结果,将石膏水泥比、掺砂率、掺水率和硼砂含量4个参数作为自变量,单轴抗压强度、抗拉强度、抗压抗拉比、弹性模量作为因变量。对各力学参数与影响因素建立多元线性回归方程,如公式(6)所示:
(6)
式中:σc为抗压强度,MPa;σt为抗拉强度,MPa;σc/σt为抗压抗拉比;E为弹性模量,GPa;a为石膏水泥比;b为掺砂率,%;c为掺水率,%;d为硼砂含量,%。
4.2 白云岩相似材料最优配比的确定
岩石相似模拟试验和其他力学模拟试验都需要遵循相似判据。通过平衡、几何、物理及边界条件方程得出了相似材料选取的主要标准如公式(7)[12]:
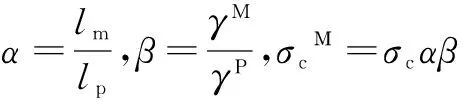
(7)
式中:lP为原型岩石尺寸,mm;lm为相似模型的尺寸,mm;α为几何相似系数;β为重度相似系数;γP为深部巷道白云岩的天然重度,kN/m3;γM为模型的干重度,kN/m3;σc为原型岩石的单轴抗压强度,MPa;σcM为相似模型的单轴抗压强度,MPa;σt为原型岩石的抗拉强度,MPa;σtM为相似模型的抗压强度,MPa;E为原型岩石的弹性模量,GPa;EM为相似模型的弹性模量,GPa;μ为原型岩石的泊松比;μM为相似模型的泊松比。
根据地质资料,矿山深部白云岩的主要力学参数结合相似判据得出相似试件的力学参数如表6所示。

表6 白云岩及相似材料主要力学参数Table 6 Main mechanical parameters of dolomite and dolomite similar materials
将得到的相似模型力学参数带入公式(6)中得出相似材料的原料最优配比见表7。

表7 多元线性回归模型确定的材料配比Table 7 Proportion of materials determined by multiple linear regression model
4.3 相似试件脆性指标的验证
白云岩具有明显的脆性,表现出较强的岩爆特征,为了确定模型试件的相似性,就试件的脆性展开定性分析。目前关于岩石脆性描述的指标有多种,包括基于应力应变曲线的脆性指标、基于破坏过程中能量变化的脆性指标、基于抗压抗压比的脆性指标,结合3种判据来对相似试件的脆性展开验证。
1)基于抗压抗拉比的的岩爆倾向性判断
试件的抗压强度σc和抗拉强度σt之比(抗压抗拉比)为脆性系数,反映了岩石的脆性程度。脆性系数的判据指标为[13]:
当σc/σt<14.5时有强烈岩爆倾向;当14.5≤σc/σt<26.7时为中等岩爆倾向;当26.7≤σc/σt≤40时为弱岩爆倾向;σc/σt>40时无岩爆倾向。
2)基于峰前弹模和峰后弹模比的岩爆倾向性判断[14]:
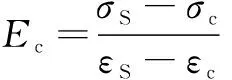
(8)
式中:E0为试件的弹性模量,GPa。
当B≤1.0时有强烈的岩爆倾向;B>1.0时无岩爆倾向性。
3)基于峰值前后应力-应变曲线所包络面积比的岩爆倾向性判[15]:
Wcf=F1/F2
(9)
式中:F1为峰值前区的面积;F2为峰值后区的面积。
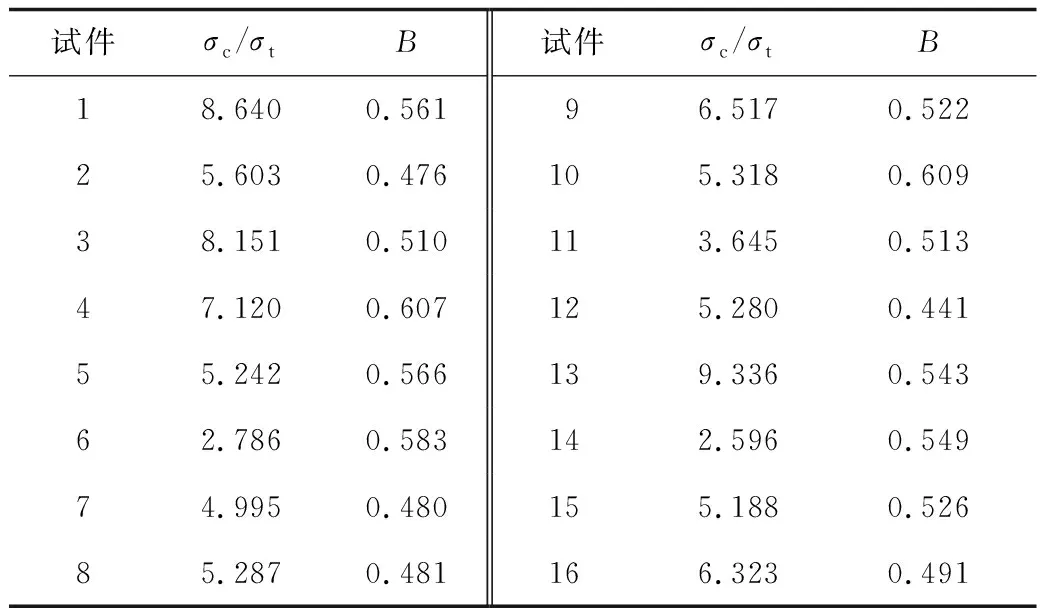
当Wcf>3.0时为强岩爆倾向;2.0 以第16个(16#)试件为例,其单轴压缩破坏的应力-应变曲线如图3所示。 图3 典型σ-ε关系曲线(试件16#)Fig.3 Typical σ-ε relationship curve(test specimen16#) 经计算,16#峰值前区的面积与峰值后区面积比为Wcf=3.168。 表8为相似材料岩爆倾向性差别情况,如表8所示,经单轴抗压强度试验和巴西劈裂试验计算出试件的抗压抗拉比,比值均小于14.5,结合应力-应变曲线计算出试件弹性模量和降模量的比,比值均小于0.7。 表8 相似材料岩爆倾向性判别Table 8 Discrimination of rock burst tendency of similar materials 通过3个岩爆性指标验证,相似试件表现出较强的岩爆倾向,可以很好地表现白云岩的脆性特征,是理想的相似试件。 1)以细砂、水泥、石膏、硼砂和减水剂为原料,采用正交设计方法制定了4因素4水平试验方案,通过单轴抗压试验和巴西劈裂试验得到单轴抗压强度、抗拉强度、弹性模量等力学参数,各力学参数分布范围基本满足相似模拟试验的要求。 2)采用方差和极差2种分析方法并结合主效应贡献图对4个影响因素的敏感性进行了分析,发现随着石膏水泥比(因素A)和掺砂率(因素B)的增大,单轴抗压强度σc呈现出逐级降低的趋势,掺砂率(因素B)对单轴抗压强度的影响较显著;掺砂率对试件抗拉强度影响显著,随着掺砂率(因素B)的增大,抗拉强度呈现出逐渐降低的趋势;随着掺水率(因素C)的增大,抗压抗拉比逐渐升高;随着石膏水泥比(因素A)的增大,弹性模量逐渐下降。 3)对正交试验结果进行拟合,得到各力学参数与影响因子的多元线性回归方程,结合相似原理,得出石膏水泥比3.1∶1、掺砂率59%、掺水率20%、硼砂含量0.4%以及减水剂含量0.3%时是该矿山深部白云岩相似材料的最优配比,可为地质灾害研究提供理论依据。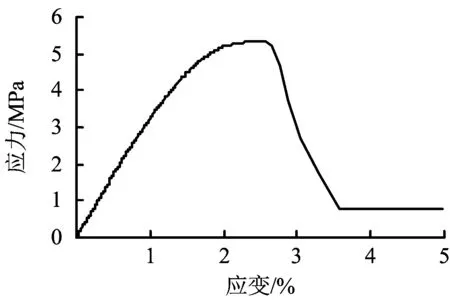
5 结论
