轴向载荷波动下海上测试管柱动力响应与安全系数分析*

孙巧雷，李 中，孟文波，冯 定，杨 行，王晓龙，涂忆柳

(1.长江大学 机械工程学院，湖北 荆州 434023；2.湖北省油气钻完井工具工程技术研究中心，湖北 荆州 434023；3.非常规油气湖北省协同创新中心 湖北 武汉 430100；4.中海石油(中国)有限公司湛江分公司，广东 湛江 524057)

0 引言

海上油气井测试过程中，测试管柱从海面上的作业平台一直延伸至泥线下的油气开采层，由于海上环境载荷引起的钻井船或平台产生漂移、摇摆、升沉等影响[1-3]，测试管柱的轴向载荷会产生较大变化。

在测试管柱系统本身复杂的受力状况下，测试管柱的安全将受到一定的影响，为保障海上测试作业的安全，开展轴向载荷波动下的海上测试管柱动力响应分析很有必要。

在现有的相关研究中[4-5]，针对管柱受到内外载荷、轴向力、弯矩、摩擦力的研究主要是集中在陆上的测试管柱，对于海上测试而言，这仅相当于对泥线下的测试管柱进行了一定的研究[6]。对于泥线上海水段的测试管柱，唐海雄等[7]以番禺5-8-1井测试管柱为例,进行了温度对管柱伸缩变化的研究；谢鑫等[8]提出了使用幅值响应算子(RAO)来计算钻井船纵荡水平运动和升沉运动的位移随时间响应的方法；戴宗等[9]针对南海深水气田测试，对流程中4个阶段的测试时间进行了优化；赵启彬等[10]针对海上高温高压井的测试工艺，开展了相关工艺的优化研究；Liu等[11]结合深水测试过程，开展了深水管柱非线性动力研究；阚长宾等[12]针对海上高温高压产层热流体产生的潜在危害，设计了1种隔热管应用于深圈闭压力控制技术；马磊等[13]根据平台类型、完井方式、测试要求等开展了海上油气井测试管柱决策系统研究；何玉发等[14]通过建立深水气井的修正参数临界携液模型，开展了深水气井测试安全携液条件的优化研究。相关研究主要是集中测试管柱的工艺、管柱连接安全、天然气水合物等方面，少有针对轴向载荷波动下的测试管柱动力学分析。因此，本文针对南海海上某井测试过程中的轴向载荷波动变化，开展了测试管柱真实轴向力研究，管柱振动理论模型分析、轴向载荷波动下的动力响应及安全系数计算分析。

1 海上测试管柱力学模型分析

1.1 测试管柱结构简介及其海水段的轴向力分析

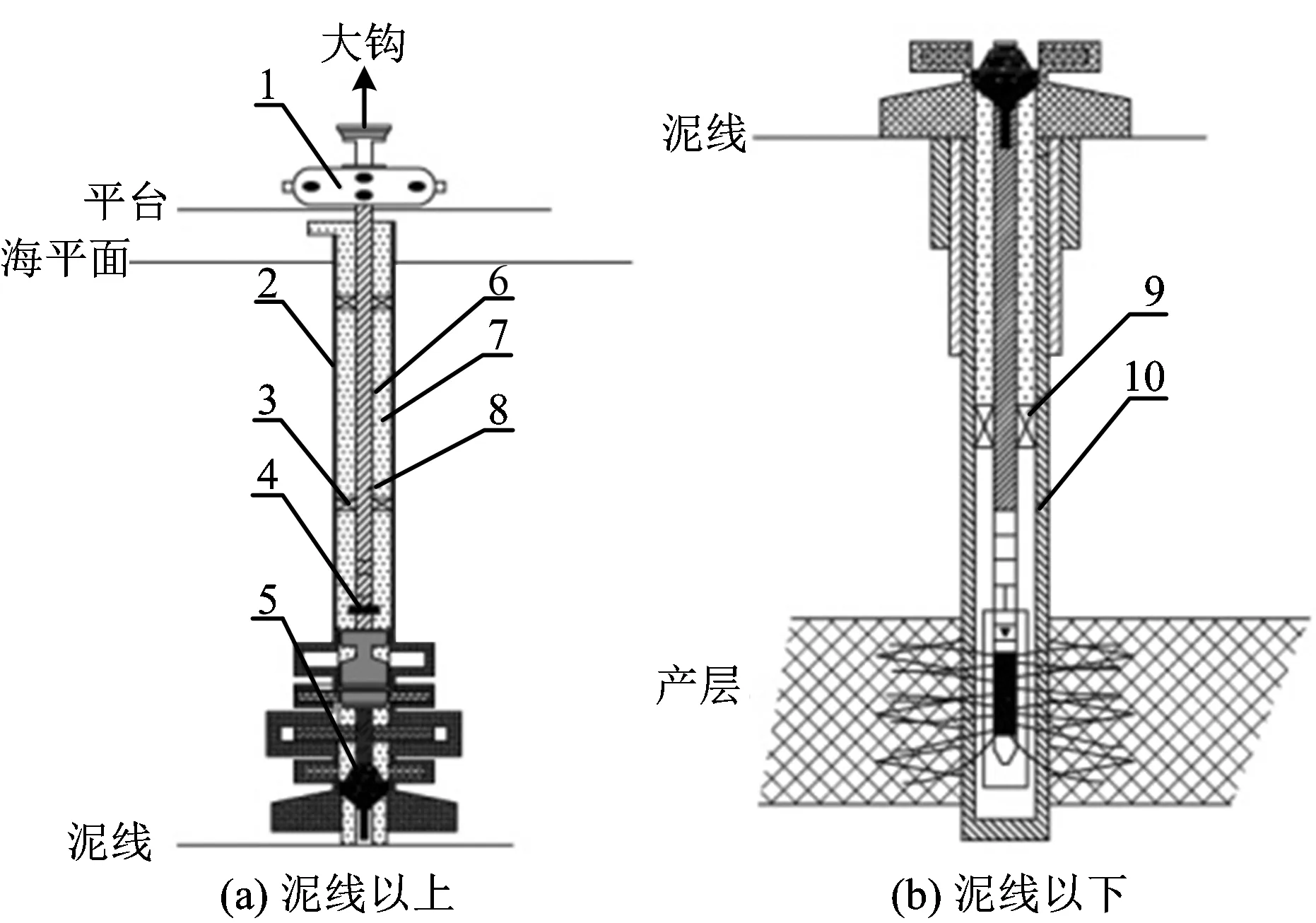
1.地面测试树；2.隔水管；3.扶正器；4.储能器；5.悬挂器；6.测试管柱；7.环空流体；8.内部流体；9.封隔器；10.套管。

测试管柱结构如图1所示。由于海上油气井产层普遍存在高温高压特性，泥线下的相关理论研究、基本结构和原理与陆地测试管柱相似，因此泥线下测试管柱分析可借助于陆上油气井管柱力学相关研究成果进行研究。泥线上(即海水段)的测试管柱位于隔水管内，其外部受到环空流体的作用，内部受到产出流体的作用；同时，在海洋环境载荷的作用，隔水管和钻井船或平台均会产生一定的沉浮运动。因此，测试管柱轴向上的轴向载荷易产生较大的波动。

对于管柱在内外压作用下的轴向力的计算，国内外围绕虚构力、液压作用力、管柱伸长压缩等进行了广泛的探讨[15-18]，笔者在前人展开研究的基础上，针对测试管柱的结构特点，增加了变径截面对轴向力Fv的影响。由于海水段的测试管柱是由多根油管及功能部件组成，存在多处如图2所示的内外变径，同时管柱的内压在测试过程中，随着不同工况(下入、开关井、射孔等)变化较大。因此，测试管柱将Fv的变化纳入考虑是必需。

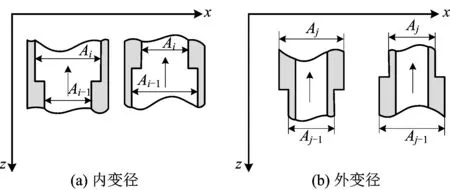
图2 测试管柱内外变径处示意Fig.2 Diameter variation at inner and outer of the string

结合测试管柱内外变径处的压力及横截面积变化，测试管柱的Fv可表示为：

(1)

式中：Fv为测试管柱的轴向力，N；n为管内径变径数量；poi为第i个内径变径处的压力，Pa；ΔAi为内变径处压力作用面积，m2；ΔAi=Ai-Ai-1；k为管外径变径数量；poj为第j个外径变径处的压力，Pa；ΔAj为外变径处压力作用面积，m2，ΔAj=-Aj+Aj-1。

此时，海水段管柱的轴向力Fz(z,t)可表示为：

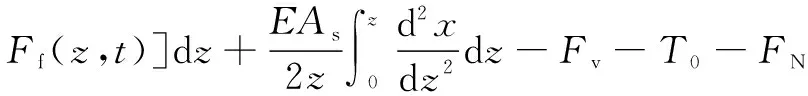
(2)

qm的计算可参考文献[19]推导的计算公式：

qm=qskf

(3)

式中：qs为管柱在空气中的线重，N/m；kf为浮力系数，kf=1-ρfo/ρs；ρs为管材密度，kg/m3。

1.2 管柱振动模型

结合完井管柱的特点，及Skalak[20]给出的圆柱薄壁输流管的经典四方程，假设测试管柱为垂直段，在考虑其内外流体与管柱内外壁间的摩阻的情况下[21-23]，测试管柱纵向振动的方程组可表示为：

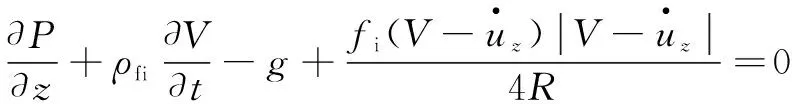
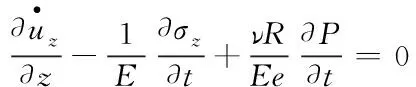
(4)

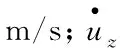
对于测试管柱纵向振动的方程式(4)，其综合考虑了测试管柱内外流体与管柱间的泊松耦合与摩擦耦合，能较好说明测试管柱在纵向振动时内部流体的的运动方程、连续性方程，管柱的轴向运动方程及管柱应力与速度间的关系。

对于海水段测试管柱的横向振动，在不考虑内部流体与管柱耦合的情况下，借助于已有的分析方法[13]，测试管柱的横向振动数学模型可以表述如下：

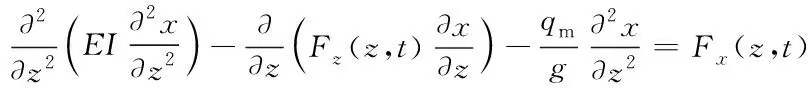
(5)

式中：EI为测试管柱截面抗弯刚度，N·m2；Fz(z,t)为测试管柱沿深度的轴向力分布，N；Fx(z，t)为内外流及隔水管等综合作用下，测试管柱沿深度横向作用力的分布，N。

对于泥线上的测试管柱，在不考虑环空流体与内外环境的换热时，环空流体的压力可按下式计算：

Pi=ρfogz+P0

(6)

式中：P0为井口环空处压力，Pa。

由式(4)和式(5)可知，海水段测试管柱轴向力的变化，不仅对测试管柱纵向振动产生影响，其对管柱横向振动也直接产生影响。为研究轴向力改变对管柱动态响应的影响，下文将针对南海某井的实际测试数据进行分析，通过构建单根油管的有限元分析模型，应用Workbench的瞬态动力学分析模块，分析不同深度处，单根油管在三角形波动轴向力作用下的位移、加速度、应力等动力响应。

2 数值模型的建立与加载

2.1 模型建立与材料属性

分析时，选取等截面单根油管(10 m)进行动力响应分析，根据南海某井的测试期间使用的油管参数，选取的管柱外径为114.3 mm、内径为85.85 mm的等截面油管，应用Workbench的Model模块直接进行建模，建模后划分的网格局部图如图3所示，该模型网格为Solid186，网格数为108 102个，节点数为583 586个。

图3 有限元模型局部网格划分Fig.3 Meshing of parts of finite element model

材料模型采用理想弹塑性模型，弹性模量E=2.06×105MPa；泊松比μ=0.3；油管选用的材料为T95；屈服强度为σs=650 MPa。

2.2 模型加载形式与载荷大小

测试管柱加载时根据课题组前期计算的管柱内外压力，加载形式为Hydrostatic Pressure，加载的内外压均随水深进行变化，其中，外压为沿z轴(水深)变化为0.012 74 MPa/m，内压沿z轴(水深)变化为0.003 8 MPa/m，参考基准面可随水深进行设置。

对于轴向力的加载，由式(2)可知，其受多种因素影响，本文针对某时段压力近似为三角波的波动形式，基于其固有频率3.125 Hz，选取了轴向力三角波动周期变化(分别为0.16，0.32，0.48，0.64和0.80 s)、幅值范围变化(分别为400，800和1 600 N)及水深不同(内外压加载为10 m管柱位于不同深度时对应的压力分布)下2个周期的三角波动进行分析，每个周期输入点为27个，每个计算步间包含5个子步，部分的加载形式的瞬态加载值如图4所示。

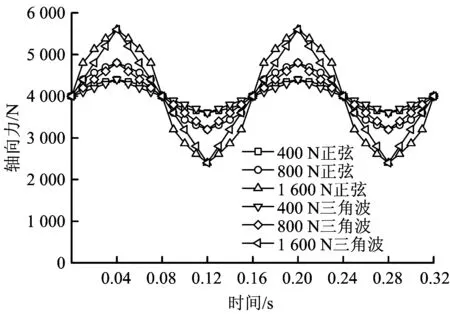
图4 轴向力加载瞬态值Fig.4 Transient value of axial force loading

3 轴向力波动下的测试管柱动力响应分析

应用Workbench进行进行瞬态分析时，其求解是基于瞬态动力学的控制方程，即：

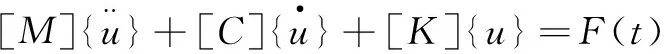
(7)

式中：[M]为结构总体质量矩阵；[C]为结构总体阻尼矩阵；[K]为结构总体刚度矩阵；F(t)为外载荷，载荷形式可为随时间变化的任意载荷。

3.1 不同波动幅值的动力响应分析

为了对轴向力不同波动幅度改变对管柱动力响应的影响，对位于水深475 m处的测试管柱，进行了波动幅值分别为10%，20%，30%的管柱动力响应分析。由于三角波作用1个周期后的响应参数几乎不变，分析时一般选取了整体数据前段的0～0.2 s的数据进行分析。

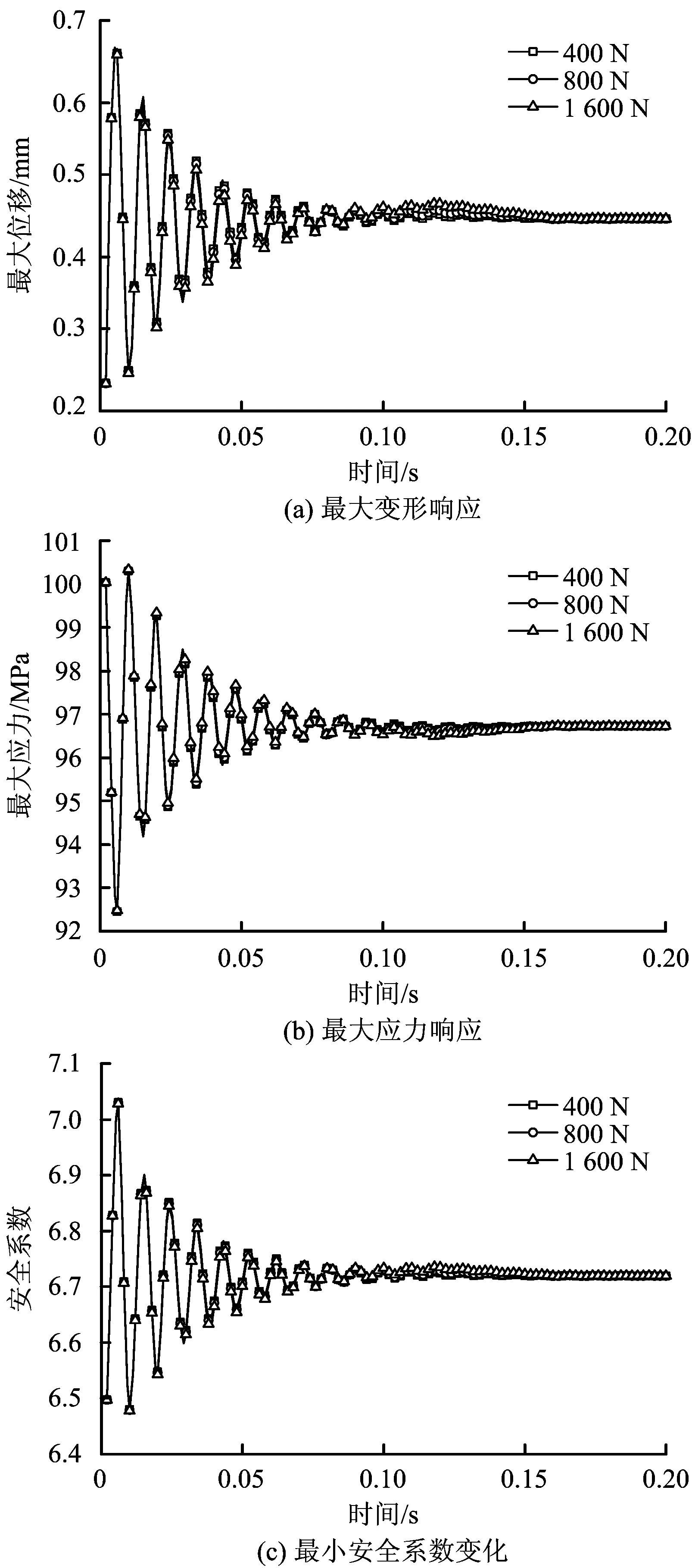
图5 波动幅值变化下的最大变形、最大应力响应及安全系数变化Fig.5 Maximum deformation，stress and safety factor under different fluctuation amplitude

波动幅值变化下的最大变形、最大应力响应及安全系数变化如图5所示。由图5可知，在轴向力的波动的幅值改变下，管柱的最大变形、最大应力的变化曲线几乎一致，相关响应在三角波作用的初期变化明显，在作用1个周期后趋于稳定；最小安全系数与最大应力的变化趋势相反，隔1个变化周期的相位差。相关结果表明，在轴向力三角波变化幅度30%内，管柱的动力响应过程基本完全一致，在弹性范围内，轴向力三角波动幅度的增加对管柱动力响应的影响不大，主要是由于轴向力波动的幅值与轴向力的平均值相比较小，材料属于弹性变化范围内。

3.2 不同水深测试管柱的动力响应分析

在测试管柱的动力响应分析，除轴向力呈三角形波动的改变，对测试管柱的单根油管上端分别位于海平面、325 m、475 m、660 m处，轴向力呈三角形波动下的变形、应力及安全系数响应进行分析。水深变化下的参数响应如图6所示。

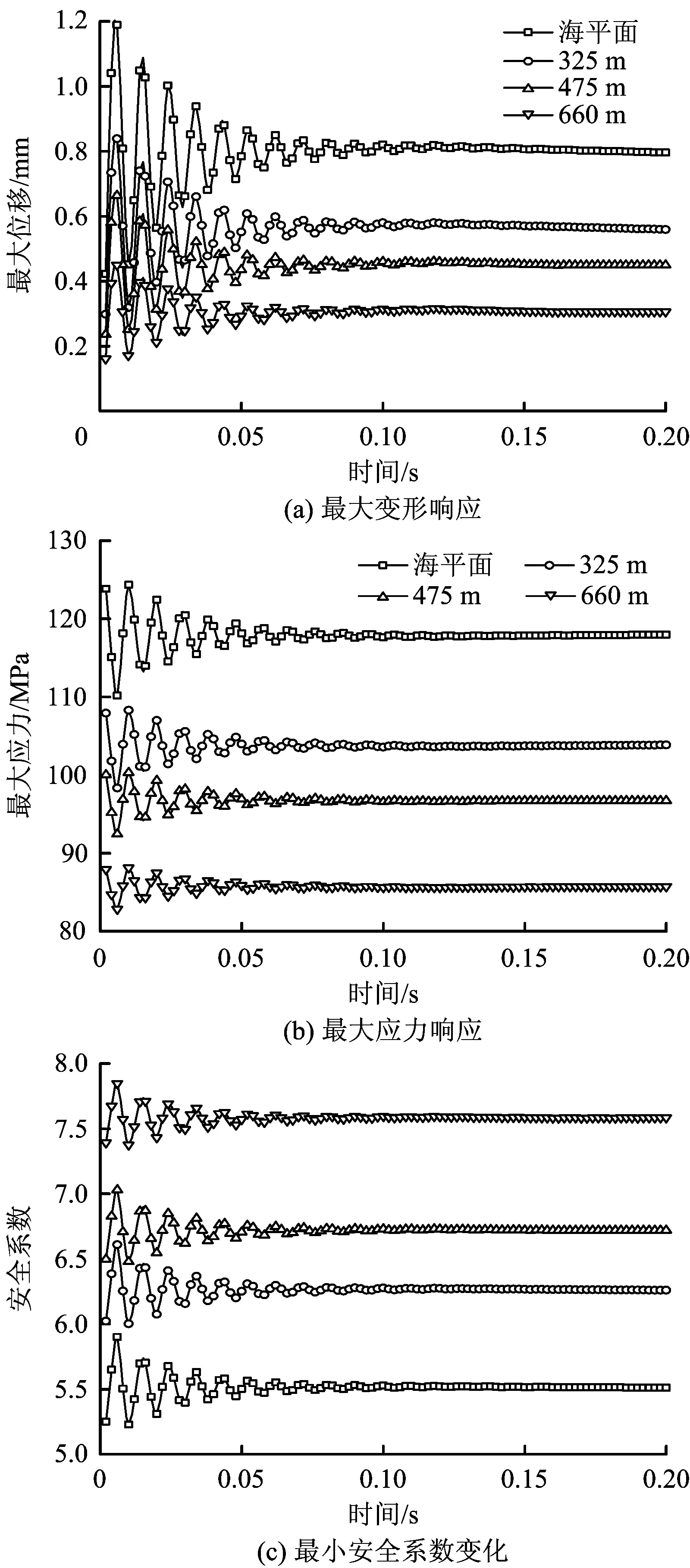
图6 水深变化下的参数响应Fig.6 Parameters response under different depth of water

由图6可知，不同深度处管柱的最大变形、最大应力、最小安全系数的响应规律基本一致，在轴向力呈三角形波动的前期，各响应结果的波动幅值较大，随着时间的增加波动幅度逐渐较小，到作用1个周期后，响应均趋于稳定，最小安全系数均大于5.0，满足现场的使用要求。相关结果同时说明，随着水深的增加，相关响应的结果参数的大小减少，对于短管柱而言，随着水深的增加，内外压的作用有助于减少管柱的响应结果参数的大小。

3.3 不同频率作用下的测试管柱动力响应分析

通过分析可知，随着波动周期的增大，响应参数的变化速率减小，因不同周期波动变化时横坐标变化幅度太大，提取的0～0.2 s数据如图7所示。同时为了对比波动幅度随波动周期的变化规律，将不同频率下的响应参数以前40个计算步进行对比，如图8所示。由图7、图8结合轴向力变化频率可知，响应参数变化与轴向力波动变化频率一致。同时，由图8可知，不同周期下，波动频率不仅影响响应参数的变化频率，同时对响应幅值的变化影响较大，随着轴向力变化频率的增大，响应参数的波动幅值增大、波动时间占比(波动时长/周期时长)增长。

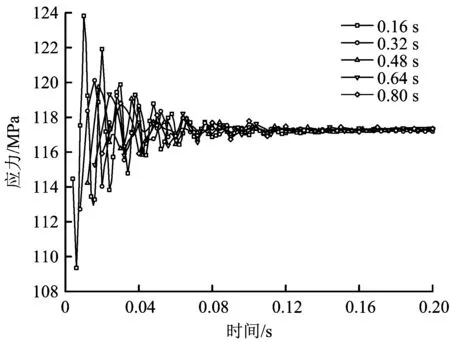
图7 最大应力随时间步变化的响应Fig.7 Maximum stress response under different computational steps

3.4 轴向力正弦波动测试管柱动力响应分析

轴向力正弦波动测试管柱动力响应结果如图9所示。通过分析可知，随着波动幅值的增大，响应参数的变化幅值增大，同时可以看出最大变形和应力的响应除整体呈正弦变化规律外，响应参数在局部上也呈减幅阻尼波动变化，且在作用的初期局部变化值较大；在作用将近1/2不同周期后，局部的响应波动变化较小，整体波动呈幅度变化较小的正弦变化。与同幅度三角波动相比，虽然最大变形量和最大应力值较三角波要小、最小安全系数较三角波要高，管柱的最小安全系数均满足现场使用要求，但应力与应变整体均呈正弦变化，正弦波动下的管柱更易出现周期性疲劳破坏。

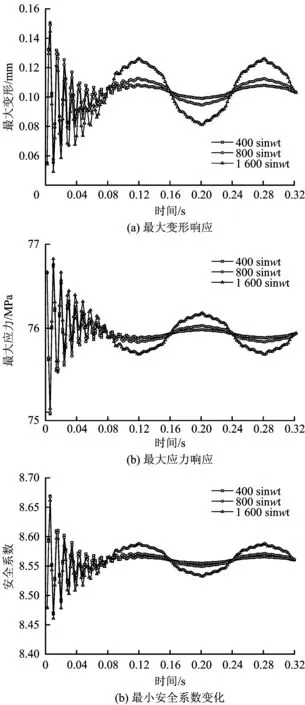
图9 参数响应随不同正弦波动幅值的变化Fig.9 Parameters response under different sine wave amplitud

4 结论

1)通过综合考虑管柱浮重系数、虚构力、张紧力、摩擦阻力、变径截面作用力等因素，对适用于海水段测试管柱的轴向力计算方法进行了确定，并建立了适用于泥线上海上测试管柱的纵向振动与横向振动力学模型。

2)轴向力三角波动下，管柱的响应参数在作用的第1个周期内波动明显，波动形式呈幅度减小的减幅阻尼振动；1个周期后响应参数趋于稳定，且波动幅值变化对响应参数的变化影响较小；正弦波动下，管柱最大变形量和最大应力值较三角波要小、最小安全系数较三角波大，但应力与应变整体均呈正弦变化，且随着波动幅值的增大，最大应力与变形、最小安全系数的响应波动增大。

3)随着水深的增加，管柱内外压增大，管柱最小应力、最大变形的响应幅值减小，但其响应规律基本不变；随着波动的频率的增大，相关参数的响应频率增大、响应幅值及波动时间占比明显增大。

4)轴向载荷不同波动形式下管柱材料的安全系数均满足使用强度要求，载荷形式影响管柱应力及变形的变化规律，波动频率与水深是影响管柱振动的主要因素。动力响应变化主要是在作用的前期，对轴向载荷波动的研究可集中在幅度较大的测试开井、关井以及下放的前期；正弦波动时，管柱的变形与应力始终随载荷变化而变化，正弦波动下的管柱更易出现周期性疲劳破坏。

5)结合管柱的动力响应分析结果，后期可进一步开展测试管柱的疲劳破坏研究。