在高中数学学习中应用函数与方程思想的探究

贾 科

(内蒙古第一机械制造(集团)有限公司第一中学1717班 014000)

一、函数与方程思想概述

函数是描述事物变化规律的一种动态模型，通过函数的对应关系可以通过一种事物的变化对另一种事物进行分析和推测.函数思想是在函数本质认知的基础上，对函数进行分析、解答和验证，并将未知的问题转化为函数问题，从而达到解决问题的目的.方程思想是通过事物间的等量关系来建立方程，通过方程来进行问题的解决.函数和方程很多时候可以进行转化，比如f(x)=g(x)，我们可以看成是两个函数y1=f(x)，y2=g(x)的交点，也可以看成是求方程f(x)-g(x)=0的解，可见函数和方程之间是互通的.掌握函数与方程思想不仅能学好数学知识，高效地解决数学问题，还能让我们掌握数学的学习和研究方法，有效地提升自主学习效率.

二、函数与方程思想在数学学习中的应用

1.在函数与方程互相转化中的应用

函数和方程在大部分时候是可以互相转化的，但是在进行转化的时候，需要注意函数的定义域，或是在函数定义域确定的情况下，运用待定系数法进行问题解答的过程中，要注意函数的类型，这样才能完整和科学地解决问题.

例1 已知2是关于a的方程2x2a-2+7xa-1+3=0的一个根，那么，求x的值和方程除2之外的根.

分析本题的是关于a的方程，已知一个根是2，将其代入可以求出未知常数x的值，然后根据方程的特点进行函数的构造，令n=xa-1，则原方程可以转化为2n2-7n+3=0，这样可以通过二元一次方程进行问题的分析和解决，最后再将求出的n值代入n=xa-1即可.

通过函数与方程的转化应用，可以有效地发挥出方程的优势，从而将函数与方程统一起来，这样就为我们提供了解答一些复杂函数与方程问题的新方法，提升了我们的思维能力，从而灵活地运用函数与方程思想进行数学知识的学习和探讨，提高我们的学习效率.

2.在不等式问题中的应用

不等式问题是高中数学知识的重要组成部分，在进行不等式知识学习的时候，往往需要借助函数与方程思想，将不等式转化为函数图象或是方程，从而运用函数与方程的性质进行不等式问题的分析和解决.函数与方程思想在不等式学习中的应用，不仅能帮助我们将所学的数学知识有机地串联起来，增强数学知识之间的联系，还能让我们深入地理解不等式的内涵，增强我们对不等式的理解，从而达到高效学习的目的.

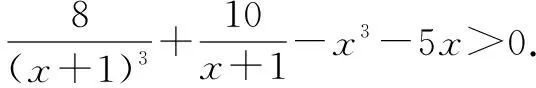
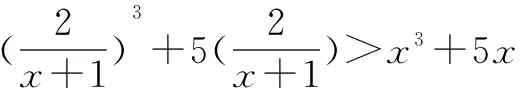
这样，通过函数与方程思想的运用，可以将复杂的不等式问题通过函数的性质转化为简单的不等式问题，从而正确地解出答案.

3.在数列问题中的应用

数列可以看做是一种定义域特殊的函数，等差数列分布在一条直线上，等比数列分布在指数函数图象上.因此，运用函数与方程的思想进行数列知识的学习和理解，更能抓住数列的本质规律，掌握数列知识，并在实际问题中进行应用.

例3 记Sn为等差数列{an}的前项和．若a4+a5=24，S6=48，则{an}的公差为( ).

A.1 B.2 C.4 D.8

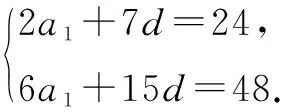
通过函数的定义域可以得到对应的值域，这和数列项数与值域是一一对应的关系，这就使得我们可以用函数与方程的思想进行数列知识的探究，并应用与解决有关数列的实际问题中，往往要比直接用代数的方法要有效得多.

总之，函数与方程思想在高中数学知识的学习和数学问题的解决中具有重要的作用，不等式、三角函数、数列等知识都与函数与方程有着密切的联系，通过数学思想的综合运用，可以将数学知识融汇贯通，从而有效地提升我们的自主学习效率.