带着理念去解题——“同一律”在高中数学解题中的一些思考

李 伟

(辽宁省鞍山市第三中学 114000)

目前师生都认识到提高数学考试成绩的重要途径之一是提高解题的准确率，所以，为减少解题出错，整理“错题本”和如何纠错等论述可谓十分流行，关于这方面的书籍、文章可以说是层出不穷、花样翻新(如文献[1])，可见人们对解决“解题出错”这一问题是非常重视的.作者通过对大量有关“错题本”类的书籍和文章进行阅读分析发现，“错题本”大都是以反映各单元、章节的题目错解、改错、给出正解等内容的积累为主要形式，缺乏高层次地对解题为何出错进行分析和理念方面的统领.为解决这一现象，通过对大量“错题本”中所列出的错误实例进行分析研究发现，题解错的原因大都是在解题变式过程中没有把握准变式前后的等价性，或解题所涉及概念公式、定理等等价性使用不当所造成的.

下面列举两个参考实例，其目的一是供查找解题出错原因及分析；二是供引入运用“同一律”理念去解题对避免解题出错所起的作用.

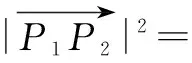
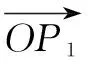
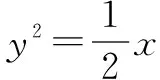
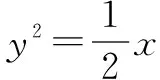
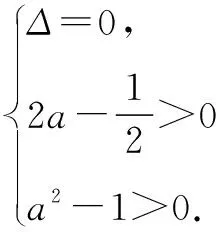
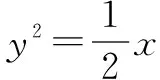
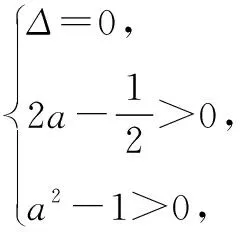
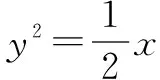
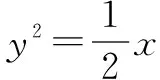
从上述错误原因分析得知，这两个实例列举出了错解类问题的两个重要类型，即：造成错解的原因是由于在使用条件，或解题变式前后出现问题.事实上，造成解题出错的原因不仅如此，还有在使用定义、公式、法则等方面因为没有注意到其相关条件、应用范围等方面导致出现错误(限于篇幅，就不再举例说明)造成的.

由此看来，如果我们就一题一意来分析解题出错原因，寻找解决方法，那呈现在我们面前的必然是支离破碎的一个个错解题目，难以找到解决问题的通性通法.试想如果跳出解题的圈子，借鉴数学哲学中的逻辑主义思想影响(数学就是逻辑的观点.见 [文献2] )，到逻辑学中是否可以找到答案.回答是肯定的，答案就是形式逻辑中的“同一律”.事实上，只要我们运用形式逻辑中“同一律”这一法则去统领解题全过程(从条件到结论)，上述错解问题就能轻松解决.换个角度说就是规避解题错误(由计算错误不考虑)的最好办法是：带着“同一律”的理念去解题.

“同一律”是什么？“同一律”是形式逻辑的基本规律之一.其基本内容是：任何一个思想与其自身是等同的.具体表述是：第一，在同一思维过程中，每个思想都必须是确定的.第二，在统一思维过程中，每个思想前后应该保持一致.

回到解题方面来，从“同一律”角度看，解题过程中的每一步骤所使用概念公式，解题过程中的转化、变式，不论是所给的题目条件，还是所使用概念、公式的内涵、外延及使用条件等，其内涵和外延都应该是一致不变的.而上述所列出现的解题出错原因恰是在解题使用条件，或变式过程中，在不自觉中改变其一致性造成的，而造成出现这类问题的原因就是缺乏解题过程中“同一性”理念的引领.可以设想，如果师生是带着“同一律”的理念去解上述所列问题一、二，带着“同一律”的理念去思考前后变式，那一定会在解题过程中提醒条件使用、每步变式(变形)是否和之前的条件式内涵、外延等相互一致，并对一致的保留下来；不一致的再将其设法改造、补充成相一致的.显然，这样做就不会出现上述解题错误了.

另外，如果师生经常性、习惯性地带着“同一律”理念去解题，时常提醒解题变换过程、使用条件等前后是否满足“同一律”，必然会在提高解题正确率的同时，也养成了一种严谨的解题思维习惯，而这种素养的迁移对从事其它工作也会受益匪浅.

当然，还需要说明的是，由于带着“同一律”理念去解题是建立在正确的概念、公式基础上的，所以在平时概念、公式等学习过程中，把握准内涵、外延；准确理解把握概念、公式运用范围(也就是强调打好知识基础)等显然是必不可少的，因为这些是运用“同一律”指导正确解题的前提.

到此，通过上述论述，大家一定会对带着“同一律”理念去解题这一思考的重要性和必要性有所认识，对运用这种理念能确保在解题过程中对题中涉及的条件使用的一致性等，能回避解题过程中可能出现各种错误所起的作用等给出一定赞同.这就是本文目的所在，希望本文对各位师生正确解题能有所帮助.