带线性记忆的弱阻尼吊桥方程拉回吸引子的存在性
2018-11-28王芳平马巧珍
王芳平, 马巧珍
(西北师范大学 数学与统计学院, 兰州 730070)
0 引 言
非自治系统在自然科学许多领域应用广泛, 目前已取得许多研究成果. Chepyzhov等[1]提出了一致吸引子的概念. 研究表明, 一致吸引子的存在性依赖于系统解算子的紧性, 但当时间趋于∞时, 一些非自治系统的轨道是无界的, 所以一致吸引子的一些经典理论已不再适用于该系统, 于是又提出了拉回吸引子的概念, 拉回吸引子定义为从-∞远处吸引解的参数族, 即初始时刻是-∞, 而最终时刻是固定的.
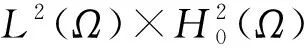
设Ω是2中具有适当光滑边界∂Ω的有界开区域, 考虑如下带线性记忆的弱阻尼吊桥方程:
(1)
解的渐近行为, 其中:u(x,t)是未知函数, 表示桥面在竖直方向的振动;α是正常数;ku+表示恢复力,k>0是弹性系数;u+=max{u,0}是u的正部,u0:Ω×(-∞,0]→表示u的过去历史;μ是记忆核;νut表示黏弹性阻尼,ν>0是一个给定的正常数;h(·)∈;L2(Ω))是外力项;τ=[τ,+∞).
首先将方程(1)转化为一个确定的非自治动力系统. 为此, 需引入表示历史位移的变量, 即
η=ηt(x,s)=u(x,t)-u(x,t-s), (x,s)∈Ω×+,t≥τ.
(2)
于是
(3)
(4)
相应的边界条件为
u=Δu=0, (x,t)∈Γ×+,η=Δη=0,x∈Ω,t≥τ,
(5)
初值条件为
u(x,τ)=u0(x),ut(x,τ)=u1(x),ηt(x,0)=0,ητ(x,s)=η0(x,s),
(6)
其中: 当x∈Ω时,u0(x)=u0(x,τ),u1(x)=∂tu0(x,t)|t=τ; 当(x,τ-s)∈Ω×+时,η0(x,s)=u0(x,τ)-u0(x,τ-s).
根据文献[3,7], 假设非线性项f∈C2(),f(0)=0, 且满足下列条件:
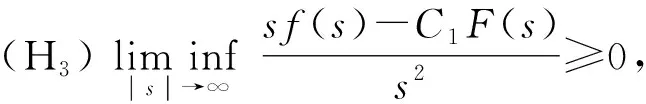
记忆核函数μ(·)满足下列条件:
(H4)μ∈C1(+)∩L1(+),μ′(s)≤0≤μ(s), ∀s∈+;
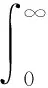
(H6)μ′(s)+k1μ(s)≤0, ∀s∈+, 某些k1>0.
目前, 关于带记忆项的动力系统已有很多成果[3,12], 但关于方程(1)拉回吸引子的存在性研究尚未见文献报道, 由于方程(1)中含有线性记忆, 故不能用拉回D-条件(C)考虑该问题. 本文用收缩函数的方法得到与问题(4)-(6)相关过程的拉回D-渐近紧性, 从而证明了方程(1)拉回吸引子的存在性.
1 预备知识
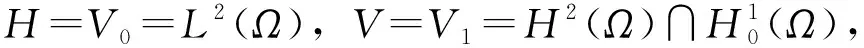
相应的内积和范数分别为
Poincaré不等式:λ1‖v‖2≤‖v‖2, ∀v∈H, 其中λ1是-Δ的第一个特征值.
设(X,d)是完备的度量空间, (Q,ρ)为度量空间, 也称为符号空间. 设θ={θt}t∈是定义在Q上的动力系统, 满足下列性质: 1) ∀q∈Q,θ0(q)=q; 2) ∀q∈Q,t,τ∈,θt+τ(q)=θt(θτ(q)); 3) (t,q)→θt(q)连续. 如果映射φ:+×Q×X→X满足: 1) ∀(q,x)∈Q×X,φ(0,q,x)=x; 2) ∀s,t∈+, (q,x)∈Q×X,φ(t+s,q,x)=φ(s,θt(q),φ(t,q,x)). 则称映射φ:+×Q×X→X是由θ诱导出的共圈.
定理1[13]设(θ,φ)为Q×X上的非自治动力系统, 假设集合族D={Dq}q∈Q为φ的拉回吸收集, 且φ是拉回D-渐近紧的. 则φ拥有拉回吸引子A={Aq}q∈Q, 且
(7)
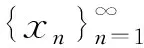
(8)
则称Φ(·,·)为B×B上的收缩函数, C表示定义于B×B上收缩函数的集合.
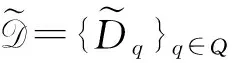
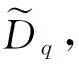
(9)
‖φ(t,θ-t(q),x)-φ(t,θ-t(q),y)‖X≤+Φt,q(x,y),
(10)
则φ在X上是拉回D-渐近紧的.
2 拉回吸引子
2.1 解的适定性
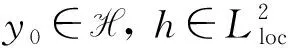
定义H中的能量泛函为
令Q=,θt(τ)=t+τ, 并定义
φ(t,τ,y0)=y(t+τ;τ,y0)=(u(t+τ),ut(t+τ),ηt(t+τ)),τ∈,t≥τ,y0∈H.
(11)
由问题(4)-(6)解的存在唯一性可知,
φ(t+s,τ,y0)=φ(t,s+τ,φ(s,τ,y0)),τ∈,s,t≥τ,y0∈H.
且对任意的τ∈,t≥τ, 式(11)定义的映射φ(t,τ,·): H→H是连续的. 因此式(11)定义的映射φ在H上是一个连续共圈. 下面假设(;H)满足
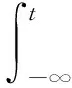
(12)
其中δ是一个正常数. 令Rδ是所有函数r:→(0,+∞)的集合, 满足
(13)
2.2 拉回吸收集的存在性
由条件(H1)可知, 存在一个正常数K1, 使得
∀u∈V.
(14)
由条件(H3)和Poincaré不等式可知, 存在一个正常数K2, 使得
∀u∈V.
(15)
用v=ut+σu与方程组(4)中的第一个方程在H中做内积, 得
结合方程组(4)中的第二个方程、 条件(H5),(H6)以及Hölder不等式, 有
(ν-σ)(ut,v)=(ν-σ)‖v‖2-σ(ν-σ)(u,v),
由式(16)可得
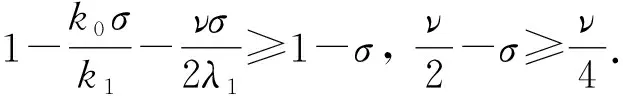
第一,优先发展RAROC较高、风险权重较低的轻资本产品。优先发展结售汇、托管、代理、承销、咨询、结算、清算等中间业务发展,提高轻资本非利息收入占比。零售贷款因其较低的风险权重,在政策允许的前提下,优先发展可改善业务结构,提高整体资本使用效率。
(18)
由式(15)可知,
将式(18)~(20)代入式(17), 整理可得
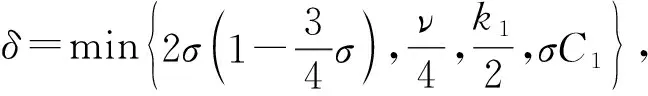
则
(21)
对式(21)从t-τ到t积分可得
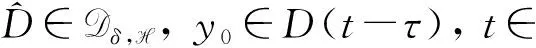
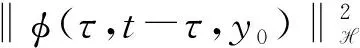
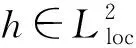
2.3 拉回吸引子的存在性
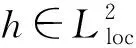
证明: 对任意的t∈, 令为问题(4)-(6)关于初值的解, 再令则w(t)和ξt(s)满足:
(22)
用eβtwt与方程组(22)的第一个方程在H中做内积, 可得
对式(23)在[s,t]上积分, 有
用eβtw与方程组(22)的第一个方程在H中做内积, 可得
对式(26)在[s,t]上积分, 有
再对式(27)关于s在[t-τ,t]上积分, 有
将式(28)代入式(25), 由β<ν/3, 且k1/2>ν(k0+1)/3, 可得
对式(26), 在[t-τ,t]上积分, 可得
将式(30)代入式(29)可得
另一方面, 对式(23)在[t-τ,t]上积分, 可得
将式(32)代入式(31)可得
综合上述估计、 结合式(33), 并记
则
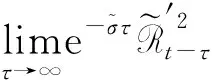
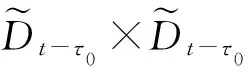
(i) 在空间L∞(t-τ0,t;V)中,un→u弱*收敛;
(ii) 在空间L∞(t-τ0,t;H)中,unt→ut弱*收敛;
(iii) 在空间L2(t-τ0,t;H)中,un→u强收敛;
(iv) 在空间L2(Ω),Lr(Ω)中, 有un(t-τ0)→u(t-τ0), 且un(t)→u(t)强收敛, 其中r≤2(p+1).
下面依次处理式(34)中的每一项. 首先, 由假设条件(i),(iii),(iv)易知,
其次, 在空间L2(t-τ0,t;L2)中, 由f(un)→f(u)弱*收敛, 并结合假设条件(ii),(iii)及文献[14], 有