一类无穷区间上分数阶微分方程边值问题正解的存在性
2018-11-28韦煜明冯春华
廖 秀, 韦煜明, 冯春华
(1. 桂林电子科技大学信息科技学院 公共课程教学部, 广西 桂林 541004; 2. 广西师范大学 数学与统计学院, 广西 桂林 541004)
0 引 言
分数阶微分方程在控制系统、 流变学、 黏弹性力学等领域应用广泛[1-4], 目前已取得了许多研究成果[5-15]. 关于有限区间和无穷区间上具有Riemann-Liouville分数阶导数α阶微分方程边值问题正解的存在性研究也得到广泛关注, 但对于半无穷区间边值问题正解的存在性及复杂系统的研究文献报道较少.
文献[14]利用Schauder不动点定理和Leggett-Williams不动点定理, 得到了分数阶边值问题:
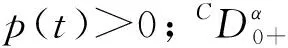
正解的存在性与不存在性, 其中2<α<3. 文献[11]利用Banach压缩映像原理和Schauder不动点定理, 得到了分数阶边值问题:
解的存在性与唯一性, 其中1<α≤2.
受上述研究的启发, 本文考虑下列分数阶边值问题:
(1)

假设如下条件成立:
(H1)f: (0,+∞)×[0,+∞)→[0,+∞),f(t,0)在(0,+∞)的任意子空间内不恒为0;

(H3) 对每个r>0, 存在函数φr∈L1(+),φr(t)≥0, 使得当|u|≤r,t∈+时, 满足

1 预备知识
定义1[1]函数y: (0, ∞)→的α>0阶Riemann-Liouville分数积分定义为
其中等式右端在(0,∞)上有定义.
定义2[1]函数f: (0,∞)→的α>0阶Riemann-Liouville分数导数定义为
定义3[1]设(X,ρ)是度量空间,T是X到X中的映射, 如果存在0<α<1, 使得对所有的x,y∈X,ρ(Tx,Ty)≤αρ(x,y)均成立, 则称T是压缩映射.

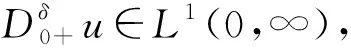
其中Ci∈(i=1,2,…,n)为任意实数,n为大于或等于[δ]的最小整数.

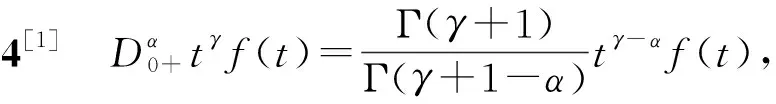

1) ‖Su‖≤‖u‖,u∈P∩∂Ω1, ‖Su‖≥‖u‖,u∈P∩∂Ω2;
2) ‖Su‖≥‖u‖,u∈P∩∂Ω1, ‖Su‖≤‖u‖,u∈P∩∂Ω2.

引理6[1]设X是完备的度量空间,T:X→X, 若存在自然数n, 使得Tn是X上的压缩映射, 则T有且只有一个不动点.

(2)

(3)
对式(3)两边积分, 得
由引理2, 得
又因为
所以有C2=0. 由u(t)的表达式有
于是, 边值问题(1)的解可表示为
证毕.
引理8若假设条件(H1)~(H3)成立, 则引理7的Green函数具有下列性质:
1) ∀(t,s)∈[0,∞)×[0,∞),G(t,s)是连续函数且G(t,s)≥0;
证明: 1) 首先根据G(t,s)的表达式, 当0 当0 (4) 显然有G(t,s)>0. 因此, 性质1)成立. 2) 根据性质1)的证明可知, 结合式(4), 性质2)显然成立. 记 其中: 定义算子A:E→E为 引理10假设条件(H1),(H2)成立, 则算子A:P→P0全连续. 证明: 取k>0, 记Bk={u(t): 0 所以Au∈C(0,+∞), 且 因此A:P→P, 其中, 因此A(P)⊂P0, 即A:P→P0. 从而由Lebesgue控制收敛定理, 有 所以A:P→P连续. 设Ω⊂P是任意一个有界集, 则存在r>0, 使得当u∈Ω时, 有‖u‖≤r. 对任意的u∈Ω, 可得 所以A(Ω)是一致有界的. 定理1假设条件(H1)~(H3)成立, 且f0<Λ1,f∞>Λ2, 则边值问题(1)至少有一个正解. 证明: 由假设条件f0<Λ1知, 存在常数r1>0, 使得对t∈+及u∈(0,r1], 有f(t,(1+tα-1)u)<Λ1u≤Λ1r1. 令Ω1={u∈P0, ‖u‖≤r1}. 对任意的u∈∂Ω1, 有‖u‖=r1, 且 又由于f∞>Λ2, 所以存在R>0, 使得对t∈[1/k,k]和u∈[R,+∞),f(t,(1+tα-1)u)>Λ2u成立. 令r2>max{r1,R/γ(k)}, 且r2,Ω2={u∈P0: ‖u‖ 因此, 对t∈[1/k,k], 有u(t)/(1+tα-1)>R, 于是由 有 由引理5知,A在P0∩(Ω2Ω1)中至少存在一个不动点, 即边值问题(1)至少存在一个正解. 定理2如果定理1的条件成立, 假设对任意的u1,u2∈E,t∈(0,∞), 存在L>0, 使得 证明: 如果定理1的条件成立, 则边值问题(1)在V中至少有一个正解. 因此只需证算子A在E上是压缩映射. 事实上, 对任意的u1,u2∈E, 由假设Lipschitz条件, 有 时, 算子A是压缩映射. 根据Banach压缩不动点定理, 边值问题(1)有唯一正解u(t)∈(0,∞).

2 主要结果