别让统计数据骗了你
2018-11-26冯海亮
冯海亮
统计数据本身并无罪,可在生活中人们往往误用统计数据.我们要学会整理、描述和分析数据,并根据数据计算的结果做出合理的推断和预测.
例1 绵阳某公司销售部统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图:
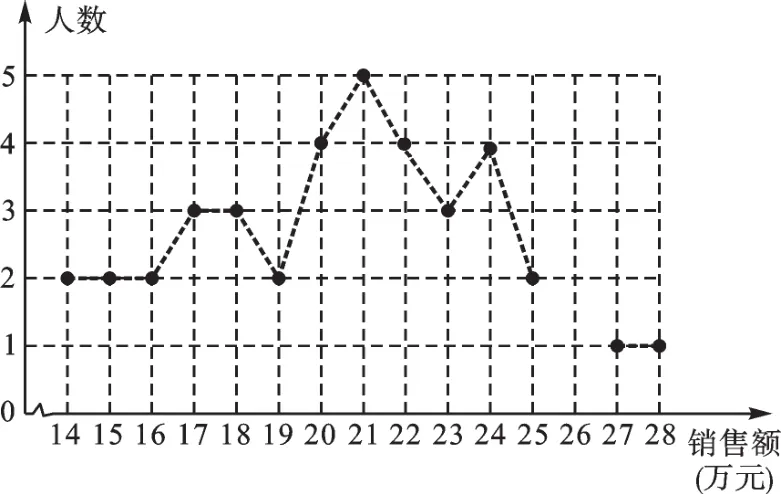
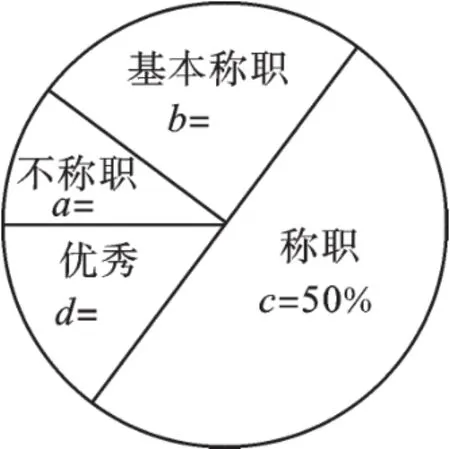
设销售员的月销售额为x(单位:万元).销售部规定:当x<16时为“不称职”,当16≤x<20时为“基本称职”,当20≤x<25时为“称职”,当x≥25时为“优秀”.根据以上信息,解答下列问题:
(1)补全折线统计图和扇形统计图.
(2)分别求“称职”和“优秀”的销售员月销售额的中位数和众数.
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励.如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖,月销售额奖励标准应定为多少万元(结果取整数)?并简述其理由.
【分析】(1)根据称职的人数及其所占百分比,求得总人数,据此求得不称职、基本称职和优秀人数的百分比,再求出优秀的总人数,从而得出销售额为26万元的人数,据此即可补全图形.(2)根据中位数和众数的定义求解即可.(3)根据中位数的意义求得称职和优秀人数的中位数,即可得出符合要求的数据.
解:(1)∵被调查总人数为:=40(人),∴不称职人员百分比为:10%,基本称职人员百分比为:100%=25%,优秀人员百分比为:1-(10%+25%+50%)=15%,则优秀的人数为:15%×40=6(人),∴销售额为26万的人数为:6-(2+1+1)=2(人),补全图形如下:
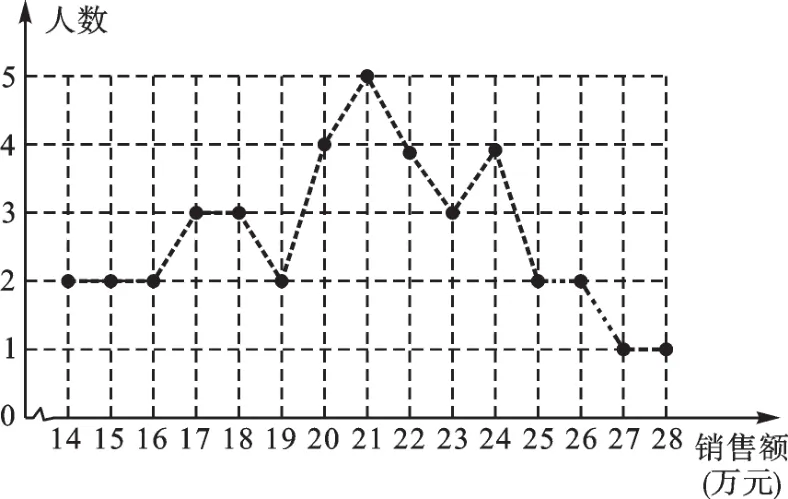

(2)称职的销售员月销售额的中位数为22万,众数为21万,优秀的销售员月销售额的中位数为26万,众数为25万和26万.
(3)月销售额奖励标准应定为23万元.
∵称职和优秀的销售员共有26人,月销售额的中位数为22.5万元,又∵结果取整数,∴要使得所有称职和优秀的销售员的一半人员能获奖,月销售额奖励标准应定为23万元.
【点评】平均数反映一组数据的“平均水平”,易受一组数据中异常值的影响;众数反映一组数据的“多数水平”,它的缺点是不具有唯一性,一组数据可能有一个众数,也可能有多个众数,也可能没有众数;中位数反映一组数据的“中等水平”,它的特点是不受异常值的影响,缺点是不能充分利用数据的信息.
例2 随机抽取某理发店一周的营业额如下表(单位:元):
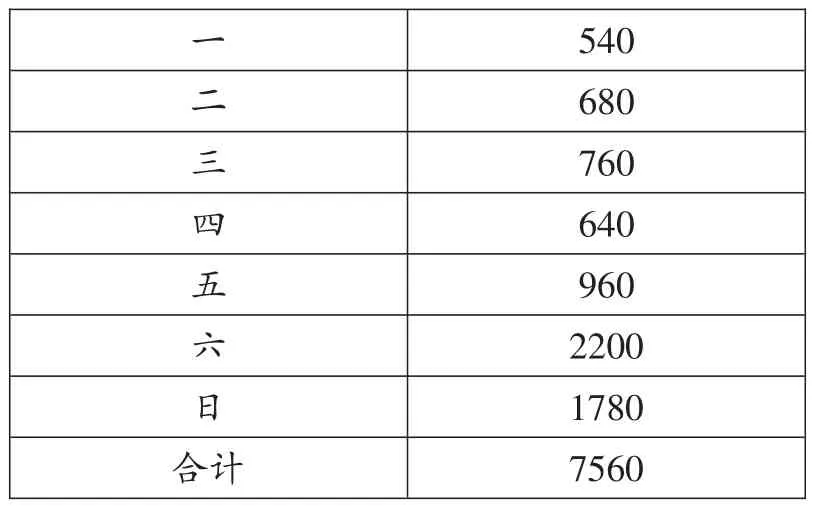
540 680 760 640 960 2200 1780 7560一二三四五六日合计
(1)求该店本周的日平均营业额.
(2)如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.
【分析】(1)根据平均数的定义计算即可.(2)从极端值对平均数的影响做出判断,可用该店本周一到周日的日均营业额估计当月营业额.
解:(1)该店本周的日平均营业额为:7560÷7=1080(元).
(2)因为在周一至周日的营业额中,周六、周日的营业额明显高于其他5天的营业额,所以去掉周六、周日的营业额对平均数的影响较大,故用该店本周星期一到星期五的日平均营业额估计当月的营业总额不合理.方案:用该店本周一到周日的日均营业额估计当月营业额,当月的营业额为:30×1080=32400(元).
【点评】本题主要考查算术平均数及由样本估计总体,解题的关键是掌握算术平均数的定义与用样本估计总体思想的运用.
例3 某中学九年级甲、乙两班分别选5名同学参加“奋发向上,崇德向善”演讲比赛,其预赛成绩如图所示:
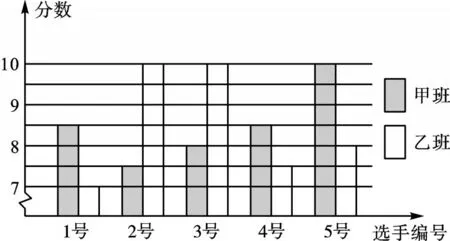
(1)根据图填写下表:
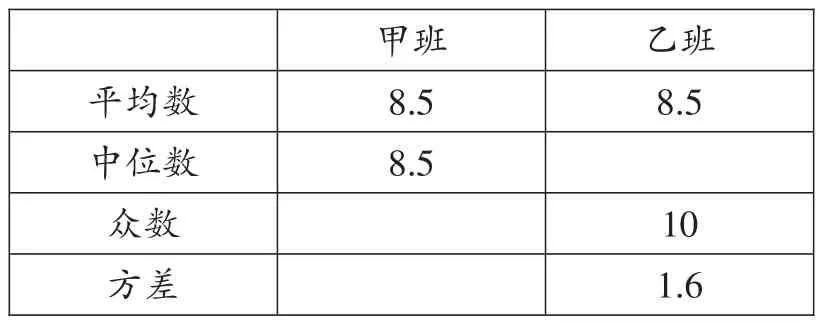
10 1.6平均数中位数众数方差甲班8.5 8.5乙班8.5
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪班的成绩较好.
【分析】(1)利用条形统计图,结合众数、方差、中位数的定义分别求出答案.(2)利用平均数、众数、方差和中位数的定义,分析得出答案.
解:(1)甲的众数为8.5,方差为0.7.乙的中位数是8.
(2)从平均数看,两班平均数相同,则甲、乙两班的成绩一样好;从中位数看,甲班的中位数大,所以甲班的成绩较好;从众数看,乙班的众数大,所以乙班的成绩较好;从方差看,甲班的方差小,所以甲班的成绩更稳定.
【点评】对于同一个问题,由于每个人观察、研究问题的角度不同,因此对平均数、中位数、众数和方差这4个统计量的关注度也不相同.
