Pattern dynamics in telegraph reaction diffusion
2018-11-24QianqianZhengFangHanZhijieWang
Qianqian Zheng, Fang Han, Zhijie Wang
a College of Information Science and Technology, Donghua University, Shanghai 201620, China
b David Geffen School of Medicine, University of California, Los Angeles, CA 90095, USA
Keywords:Pattern dynamics Stability Diffusion Memory effect
A B S T R A C T Reaction-diffusion (RD) equation was often used to investigate the pattern dynamics, but telegraph reaction-diffusion (TRD) system was seldom studied. In this paper, the Izhikevich model was modified to explain some biological mechanisms by RD and TRD in neuronal cluster. Then a new condition under which the system loses stability was proposed and the effect of parameters,diffusion, memory and steady state were considered on the process of neuronal spiking. The method presented is a novel approach to investigate the pattern dynamics of biological systems.Finally, simulations are carried out to validate our theoretical results.
The pattern dynamics was first investigated and interpreted in a reaction-diffusion (RD) system and was used successfully to explain some biological mechanisms [1]. The telegraph reactiondiffusion (TRD) equations are a pair of coupled, linear differential equations that describe the voltage and current on an electrical transmission line with distance and time, which describe a diffusion process with a finite velocity of propagation, and onedimensional (1D) TRD equation was formulated by Ohm’s law and solved by semianalytic method [2–5]. And it turned out that the corresponding TRD is as suitable as or even more ordinary diffusion equation to model RD system in biological, cosmic-ray transport, and social systems [6–8]. However, TRD system was just investigated in 1D or simple analytical solution was given in different fields [2–8].
To understand the dynamical mechanism of neuronal spiking in brain, many mathematical models of spiking neurons have been proposed to explain a wide variety of neuronal spiking behaviors [9–12]. And a model with particularly low implementation complexity and high model fidelity by combining the dynamics of Hodgkin–Huxley model and the computational efficiency of integrate-and-fire neurons, namely the Izhikevich spiking neuronal model was formulated [13]. Then the effect of the chaotic resonance and the resetting parameters on the typical spike behaviours are analyzed [14, 15] and an improved silicon neuron circuit and fractional-order was proposed on basis of Izhikevich model [16, 17]. But the TRD equation was seldom considered in the Izhikevich spiking neuronal model.
In this paper, we investigated the dynamics behavior of a modified Izhikevich spiking neuronal model with telegraph equation, proposed a new instability condition in two-dimensional (2D) TRD on the basis of neuronal spiking, analyzed the stability of the system under different conditions and further explained some biological mechanisms in neuronal spiking for pattern formation.
The Izhikevich model, proposed to describe the variation of state in a neuron [10, 13], consists of two variable differential equations with a jump of state: ifmV, thenand.
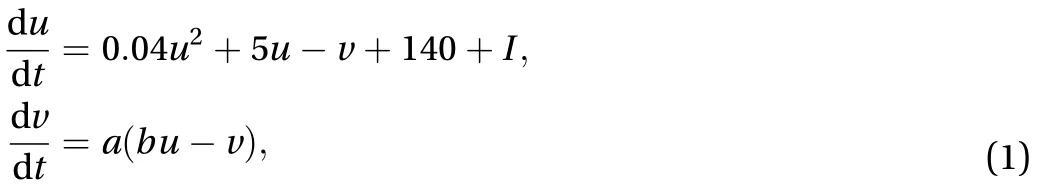
As we all know that ionic diffusion is ubiquitous and plays an important role in the membrane potential of the neuron and the membrane recovery. Dendrites play the crucial role in collecting the signals from other neurons and transmitting them to soma,while it takes time to reach the threshold, which means the memory effect also exists in this system. Therefore, the effect of diffusion and memory on the system is considered in this system, and then the TRD [2] can be written as
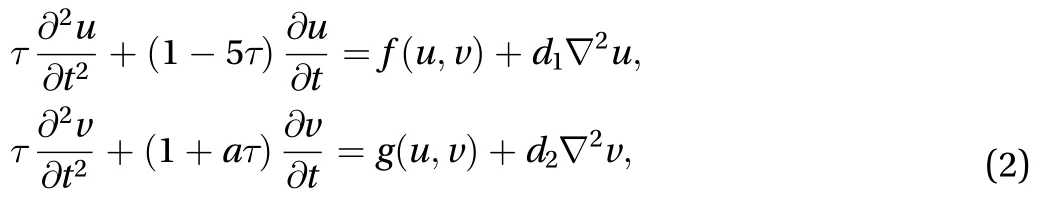
A linear stability analysis for TRD system in Eq. (2) was performed atwhich satisfied. For the stability of this spatially uniform solution, we consider a perturbation of the form
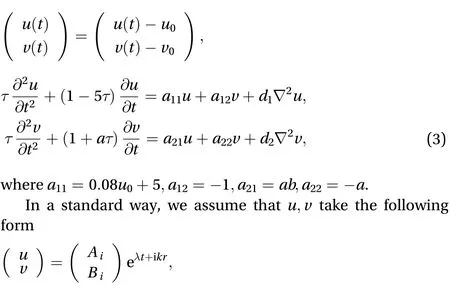
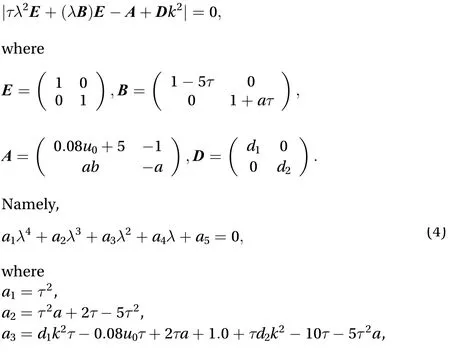

First, the system with neither diffusion nor memory effect,namely, will be considered and the characteristic equation is
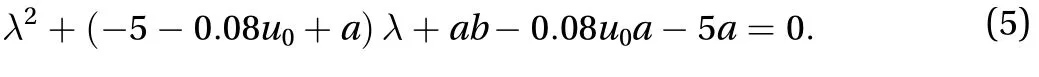
It is easy to find that the system is stable if and only if. If not, the system is unstable.
Secondly, the effect of diffusion on the system will be studied,namely, on the basis of the stable conditions.

Finally, we consider the stability of the system whose characteristic equation is
The stable condition corresponds tonamely, Routh–Hurwitz criteria condition is true for the system. And for Turing instability, at least one of Routh–Hurwitz criteria conditions is violated, i.e., the real part of, at least, one of the roots of Eq. (4) is positive.
Here we will give the stability and the pattern formation of the modified Izhikevich model to illustrate the above theoretical analysis and try to find new interesting complex dynamical behaviors by using numerical simulations. Our simulation results are created using MATLAB by the finite difference method and MAPLE. For the pattern formation, all our numerical simulations employ zero-flux boundary conditions in two spatial dimensions and the time step and space step are set asand,respectively. It can be found that there are two steady states, we supposedis stable andis unstable from Eq. (5). In general, there are two steady states in this model, one is stable and the other is unstable, corresponding to the mutual transformation between silence and excitation. If only one steady state exists, the neural system will be in silence or excitation all the time, which means the neural system disease occurs.Here the steady state is described by the initial value. In each excitatory cell,[5]. And chattering occurs (Fig. 1(a)) in a neuron whenand it changes from chattering(cortical excitatory neurons) to fast spiking (cortical inhibitory interneurons) asvaries from-40 to-65 (Fig. 1(a)-(c)). Andmakes the frequency of spiking change (Fig. 1(a), (d)-(f)). But initial value and parameters show little influence on dynamical behavior and pattern formation in normal parameter region(Figs. 1, 2). In a word, the dynamical behavior changes slightly in normal range.
We mainly consider the system is pathological. On the one hand,varies abruptly when the extra stimulus (initial value) is strong, which means information transfer occurs (Fig. 3(a), (c)),and become stable (Fig. 3(a)) after spiking. The risk of nerve disease may exist if the voltage varies slowly and stay in silence all the time (Fig. 3(a), (b), (e), (f)). In addition, we find the spike occurs attime unit (Fig. 3(a), (c)) in our simulation, which is independent of the time scale of the recovery variable(Fig.3(c), (f)), the sensitivity of the recovery variable(Fig. 3(c), (e))and the after-spike reset value of the membrane potential (Fig.3(a), (c)). However the excitatory input current plays an important role in the spiking time (Fig. 3(a), (d)). On the other hand, if the extra stimulus is weak or none, the nerve cell will stay silent all the time, which is stable (Fig. 3(b)). In conclusion, the parameters and initial value exert a tremendous influence on dynamical behavior in pathological range, which can be treated as a reference to help the doctors with a diagnosis.
As we know that Turing instability occurs on the basis of a stable system. Here the stable state corresponding to the system goes back to the stable state after spike and the steady states
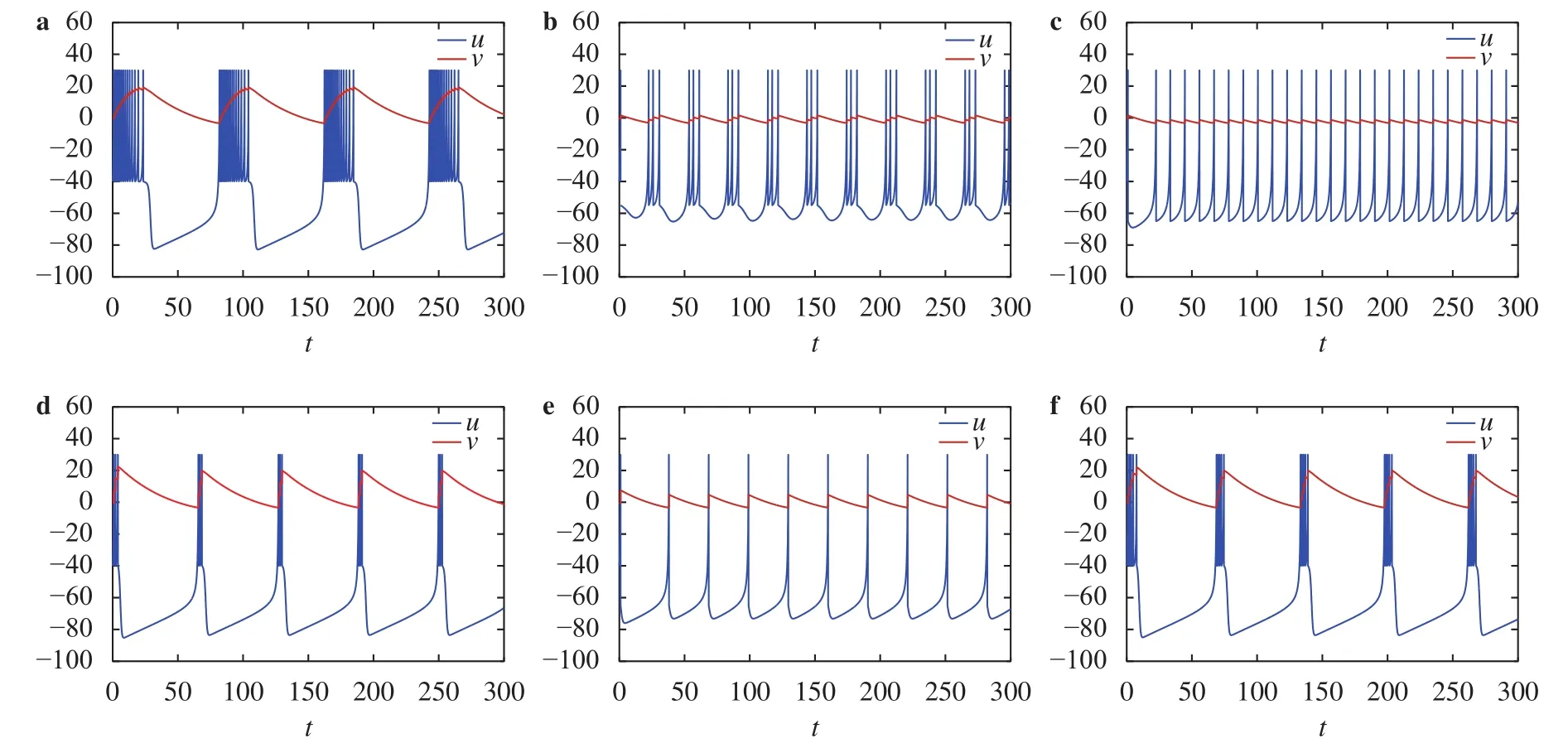
Fig. 1. Oscillations of the modified Izhikevich model with different parameter settings: a. And the initial value for all the figures are being set at
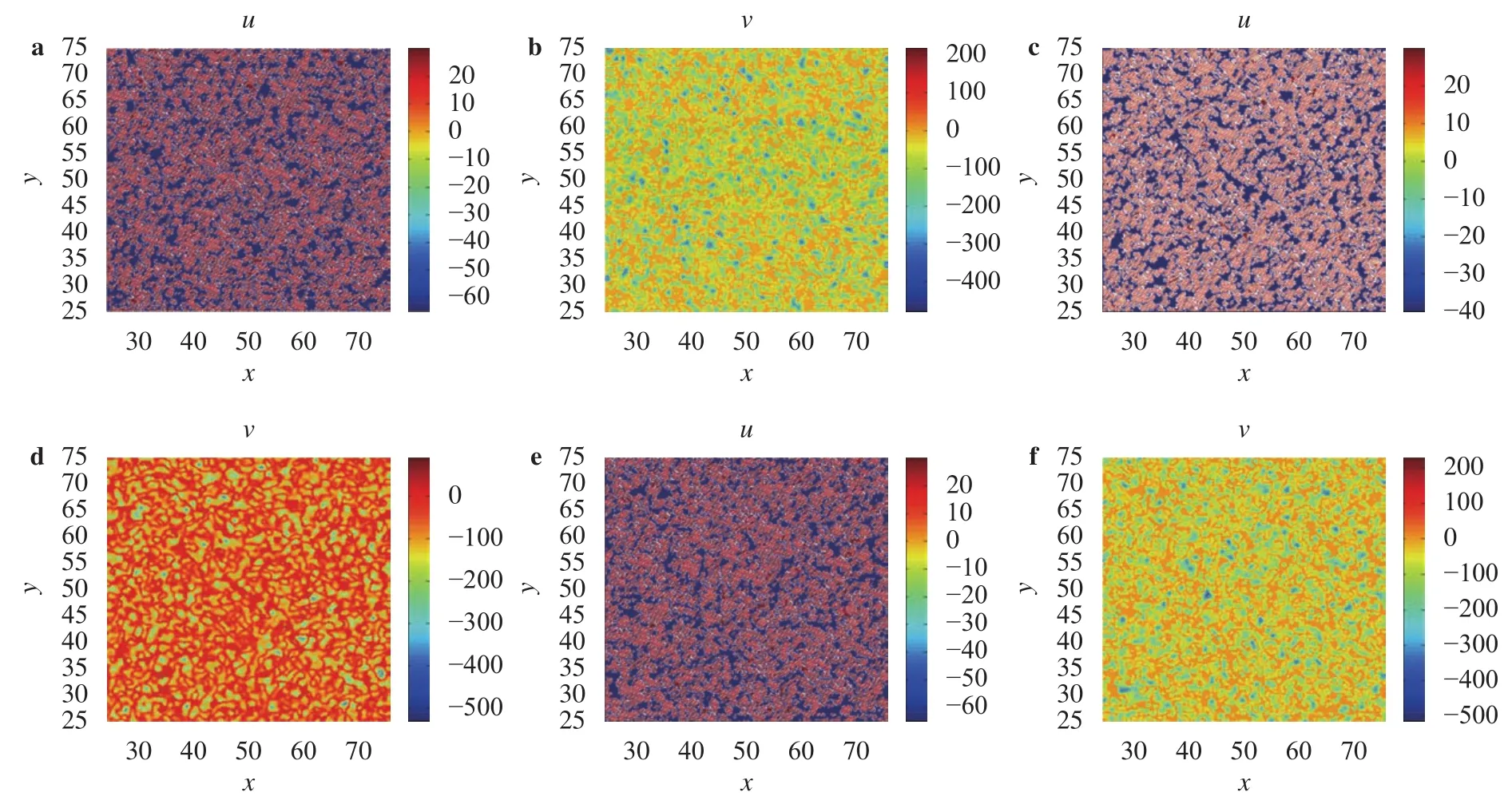
Fig. 2. Pattern formations of the modified Izhikevich model with different parameter settings: a, b a=0.02, b=0.2, c=–65, d=2, d1=0.1, d2=0.15,c, d a=0.02, b=0.2, c=–40, d=8, d1=0.1, d2=0.15, e, f a=0.02, b=0.2, c=–65, d=8, d1=0.1, d2=0.15.
are both stable when the parameters is set as, the number of neurons isand the pattern formation shows the state of every neuron. As a result of a spike, a spot pattern indicates a spike when the instability occurs in our simulation and the pattern formation describes the states of all neurons, who contribute to the information transfer at the same time and different sites. And the diffusion is crucial to the shape of pattern formation (Fig. 4(a)-(d)), which also means the number of spikes are much more if the diffusion of a membrane recovery variableis slower. In addition, the excitatory input current influences the number of spike (Fig. 4(c)-(f)) and accords with positive feedback mechanism. But the diffusion and the excitatory input current are dispensable for the pattern formation (the number of spikes) (Fig. 5) when the system is stable.is vital for the shape of pattern formation (Fig. 6(a), (c)) when the system is unstable(Fig. 6(e)), which also makes the spiking occur, but not all the time. For the stable system (Fig. 3(f)), the effect ofis not obvious (Fig. 6(b), (d)). Of course,plays an important role in the stability of system (Fig. 6(e), (f)). But the pattern formation is more obvious in normal range (Fig. 2).
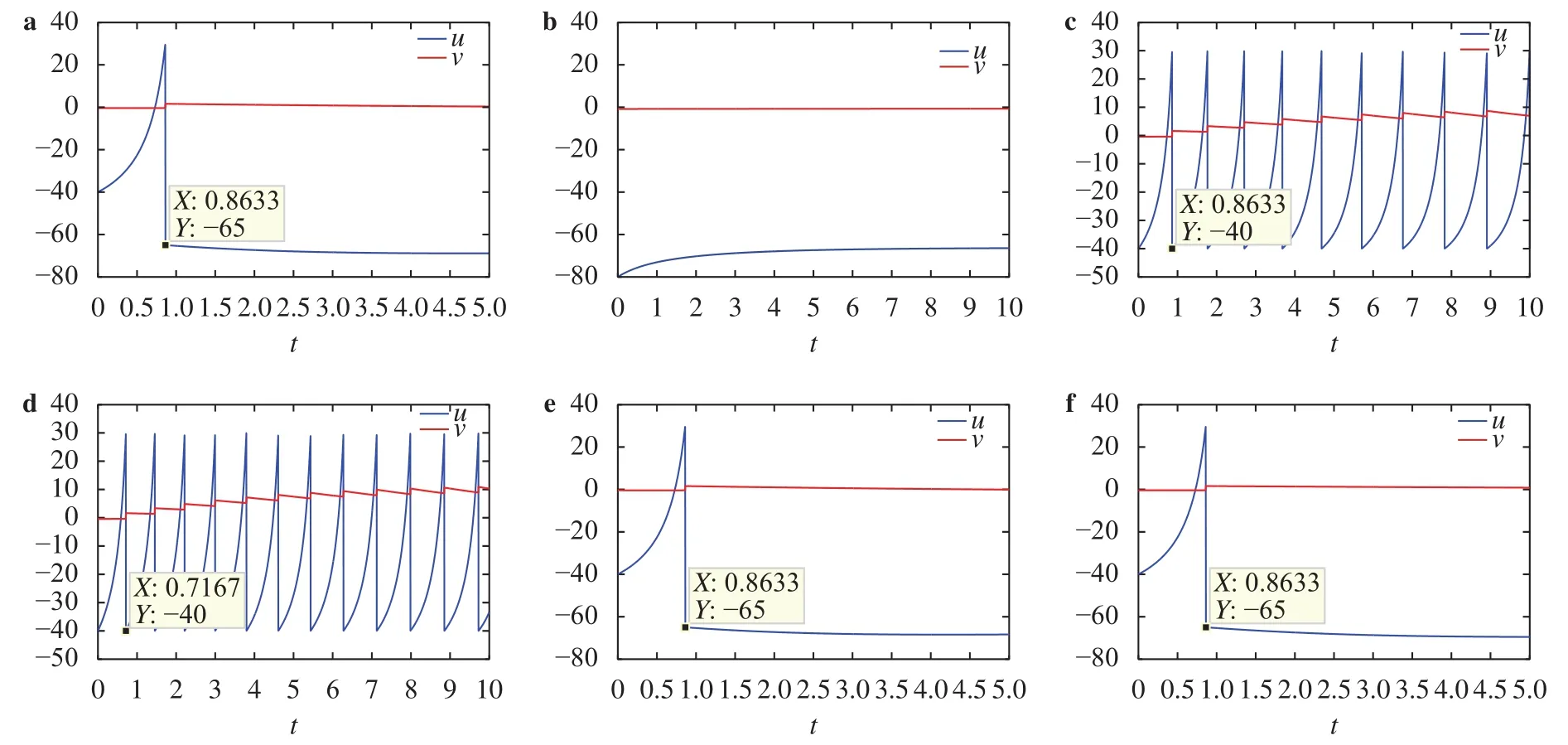
Fig. 3. Initial value for all the figures are being set at [-40, -0.4] by default. a System is unstable when a = 0.2, b = 0.01, I = 15, c = -65, d = 2,b System is stable when a = 0.2, b = 0.01, I = 15, c = -65, d = 2, and initial value [-80, -0.8], c System is stable when a = 0.2, b = 0.01, I = 15, c = -40,d = 2, d System is stable when a = 0.2, b = 0.01, I = 25, c = -65, d = 2, e System is stable when a = 0.2, b = 0.02, I = 15, c = -65, d = 2, f System is stable when a = 0.1, b = 0.01, I = 15, c = -65, d = 2.

Fig. 4. System is unstable when the initial value is set at and the parameters. a, b Pattern formation when. c, d Pattern formation when. e, f Pattern formation when.
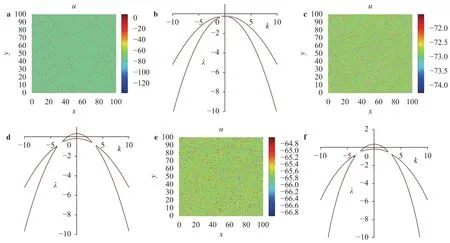
Fig. 5. System is stable when the initial value is set at and the parameters:. a pattern formation when. b Distribution of characteristic value via at when. c Pattern formation when. d Distribution of characteristic value via at when. e Pattern formation. f Distribution of characteristic value via at when.
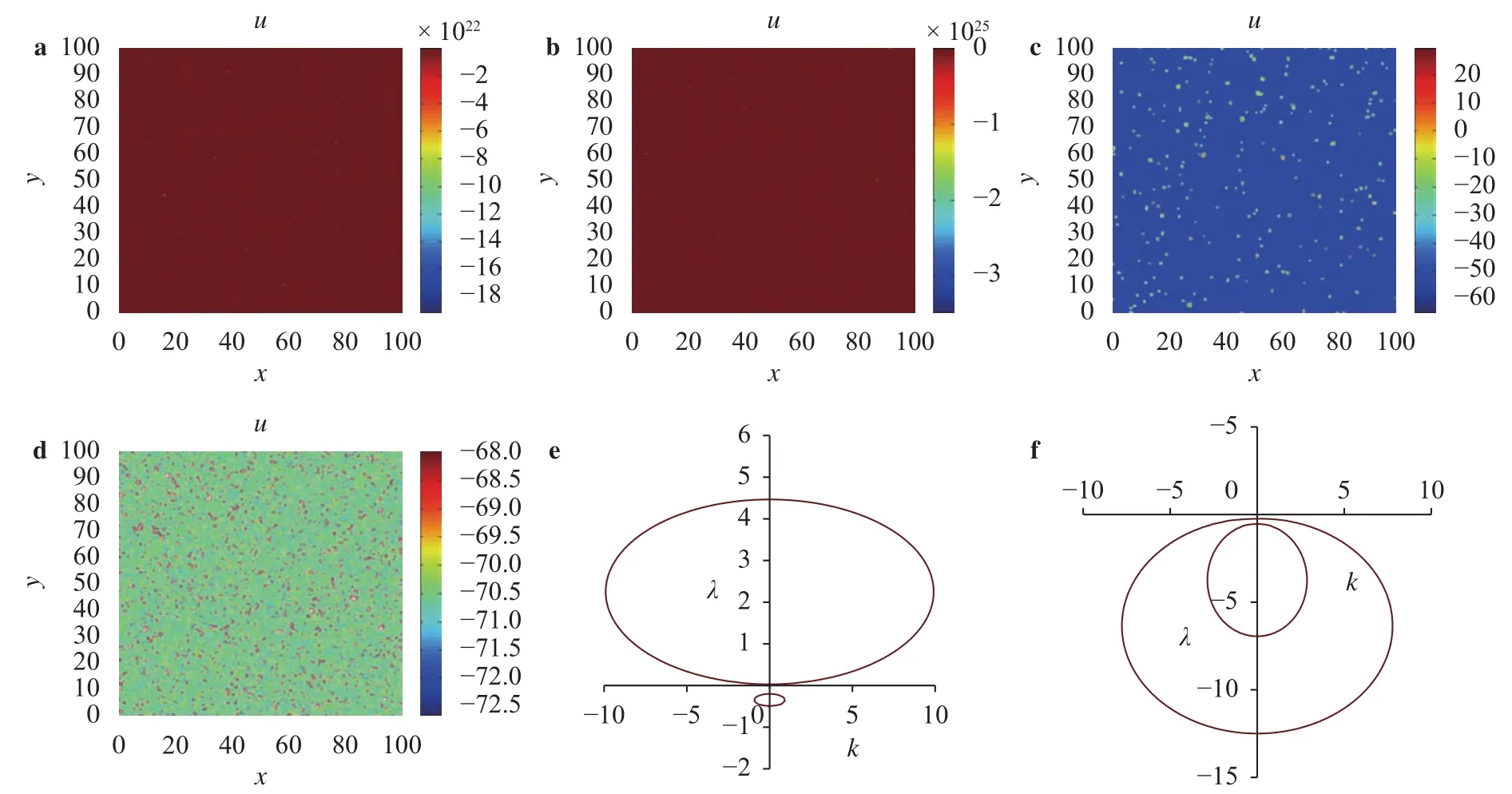
Fig. 6. Parameters are set as. a Pattern formation when and initial value is set at. b Pattern formation when and initial value is set at. c Pattern formation when and initial value is set at. d Pattern formation when and initial value is set at . e Distribution of characteristic value via atwhen. f Distribution of characteristic value via
In this article, we present a systematical analysis about the stability and the shape of pattern formation caused by memory effect, diffusion, the excitatory input current, the sensitivity of the recovery variable, the after-spike reset value of the membrane potential and steady state. The type of pattern formation describes the state of all neurons involved in the information transfer. The number of spikes will be much more when the diffusion of a membrane recovery variable is slower and the excitatory input current is proportional to the number of spikes(spot). So a spot in pattern formation means a spike occurs in neurons, and the condition of neurons can be presented by the type of pattern formation. And then our results demonstrate that the stability of neuronal system and the pattern formation can be controlled by the above factors in pathological range, which can be treated as a reference to help the doctors with a diagnosis.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grants 11572084 and 11472061), the Fundamental Research Funds for the Central Universities and DHU Distinguished Young Professor Program (Grant 17D210402), and China Scholarship Council and the Fundamental Research Funds for the Central Universities (Grant CUSF-DH-2017079).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Continuum percolation of porous media via random packing of overlapping cube-like particles
- Traffic flow and safety analysis
- Air entrainment in a vertical dropshaft with limited air supply
- Intrinsic relationship of vorticity between modes A and B in the wake of a bluff body
- An improved lattice Boltzmann model for high gas and liquid density ratio in composite grids
- A visualized study of interfacial behavior of air–water two-phase flow in a rectangular Venturi channel
