Continuum percolation of porous media via random packing of overlapping cube-like particles
2018-11-24JianjunLinHuisuChen
Jianjun Lin, Huisu Chen
Jiangsu Key Laboratory of Construction Materials, School of Materials Science and Engineering, Southeast University, Nanjing 211189,China
Keywords:Cube-like particles Porous medium Percolation Finite-size scaling analysis Simulation and modeling
ABSTRACT The pore configuration in porous medium is assumed to be the randomly distributed cube-like particles which can overlap each other in the periodic cubic domain, and the impact of particle characteristics on the percolation property of these cube-like particle packing systems is analyzed.Firstly, by combining the percolation models and finite-size scaling analysis, three numerical parameters (i.e., percolation transition width L, local percolation threshold c(L), and correlation length exponent ) for the cube-like particle systems with shape parameter s in[1.0,+∞] are derived successively. Then, based on the relation between the percolation threshold ψc in infinite space and the local percolation threshold c(L), the corresponding c with s in[1.0,+∞] are further determined. It is shown from the study that the characteristics of cube-like particles have significant influence on the global percolation thresholdc of the particle packing systems. As the parameter s increases from 1.0 to + ∞, the percolation thresholdc will go down persistently. When the surface of cube-like particles is cubical and spherical, respectively, the minimum and maximum thresholdsc,min and ψc,max are obtained.
Percolation refers to the movement and filtering of fluids through the porous media [1-3] and is a common phenomenon in material science such as filtration of water through permeable rocks, solute transfer in soil and penetration of harmful ions in cement-based materials. Percolation threshold is a mathematical definition which mainly characterizes the connectivity formation of the specified phase in multi-phase materials and usually represented by the critical fraction of research objects in the percolation models. Above this threshold, there exists a connected component in the systems and dramatic changes of material properties would occur in many practical applications.Much attention has been devoted to the study of the percolation properties of various materials [4-8]. On the microscopic scale,the interior cracks and pores in materials can be simplified to be the randomly distributed three-dimensional (3D) overlapping particles [9, 10] and the effect of crack shapes on the percolation behavior of particle systems is investigated [11]. However, the previous studies about the percolation properties of 3D particle systems are mainly based on the packing models of spheres[4, 5], spherocylinders [6], Platonic particles [7], ellipsoids [8], etc.
Cube-like particles are a group of convex particles whose surfaces can interpolate between cube and sphere, and have been widely applied in modeling colloidal suspensions [12, 13], cubic crystals [14], etc. As a new type of synthesized particles in recent years, we investigate the continuum percolation properties of congruent cube-like particle systems by combining the packing models of the overlapping cube-like particles with percolation theory. The corresponding global percolation thresholdcof infinite systems with the parametersin [1.0, +∞] are derived by us, respectively. Finally, the linear relationship between the parametersand the thresholdcare also analyzed briefly.
In analytical geometry, the surface of those cube-like particles could be represented easily by using the extension of the function for a sphere [13] as

in which, the exponentsis usually utilized to characterize the shape characteristic of cube-like particles and its value is between 1.0. Assis equal to 1.0 and +∞, the surface of cube-like particle will become spherical and cubical,respectively. In Fig. 1, the variation of the surface of cube-like particles along with the increasingsfrom 1.0is shown. In addition,ain Eq. (1) represents the size of the cube-like particles. When the surface of the cube-like particle becomes spherical,ais the radius of the particle. In the case the cube-like particle is cubical,arepresents the half of the edge length of the particle. In our study, to obtain a randomly distributed cube-like particle in 3D space, we developed another style of functions by combining with eight parameters (i.e., particle center (x0,y0,z0),Euler angles (), particle shape (s), and particle size (a))and the detail functions can be found in Ref. [11].
Percolation theory mainly considers the connected behavior of the formed clusters in the random systems of sites, bonds or particles, etc. [15-18]. In the modeling of continuum percolation in particulate porous media, the pore configurations in materials are generally assumed to be the two-dimensional (2D) or 3D overlapping particles distributed randomly. In the particle systems, the percolation is deemed to realize once we can find a connected-particle cluster that spans the system from a boundary plane to the opposite boundary plane. Next, based on the characteristics of the 3D cube-like particles, we briefly introduce a commonly searching method for the percolation cluster as Fig. 2.
① By using Monte Carlo method, we first generate a series of congruent cube-like particles in a cubic container with periodic boundaries. Both the particle volume fractionVpand particle sizeaare set in advance. The positions and orientations of particles are randomly selected and all of the particles can overlap without interference. That is to say in this process all the particle positions and orientations are totally uncorrelated.Then, we can calculate the number of the particles by

whereLis the generated container’s side length andNis the need number of particles in the container.V(a,s) represents the volume of a cube-like particle and can be obtained via

② Search for the particles which overlap with the boundaries of container (or particles) by the method in Ref. [11], and differentiate them by different symbols. If we can find a connected cube-like particles cluster that spans between one side and the opposite side of the research domain, the percolation is realized.
③ A great number of cube-like particle packing systems with specifiedVp,a,s, andLare generated, and all of them are checked by above-mentioned procedure. Then, the reliable percolation probability, symbolically represented byP(Vp,L),can be given when the number of generated systems is sufficiently large.
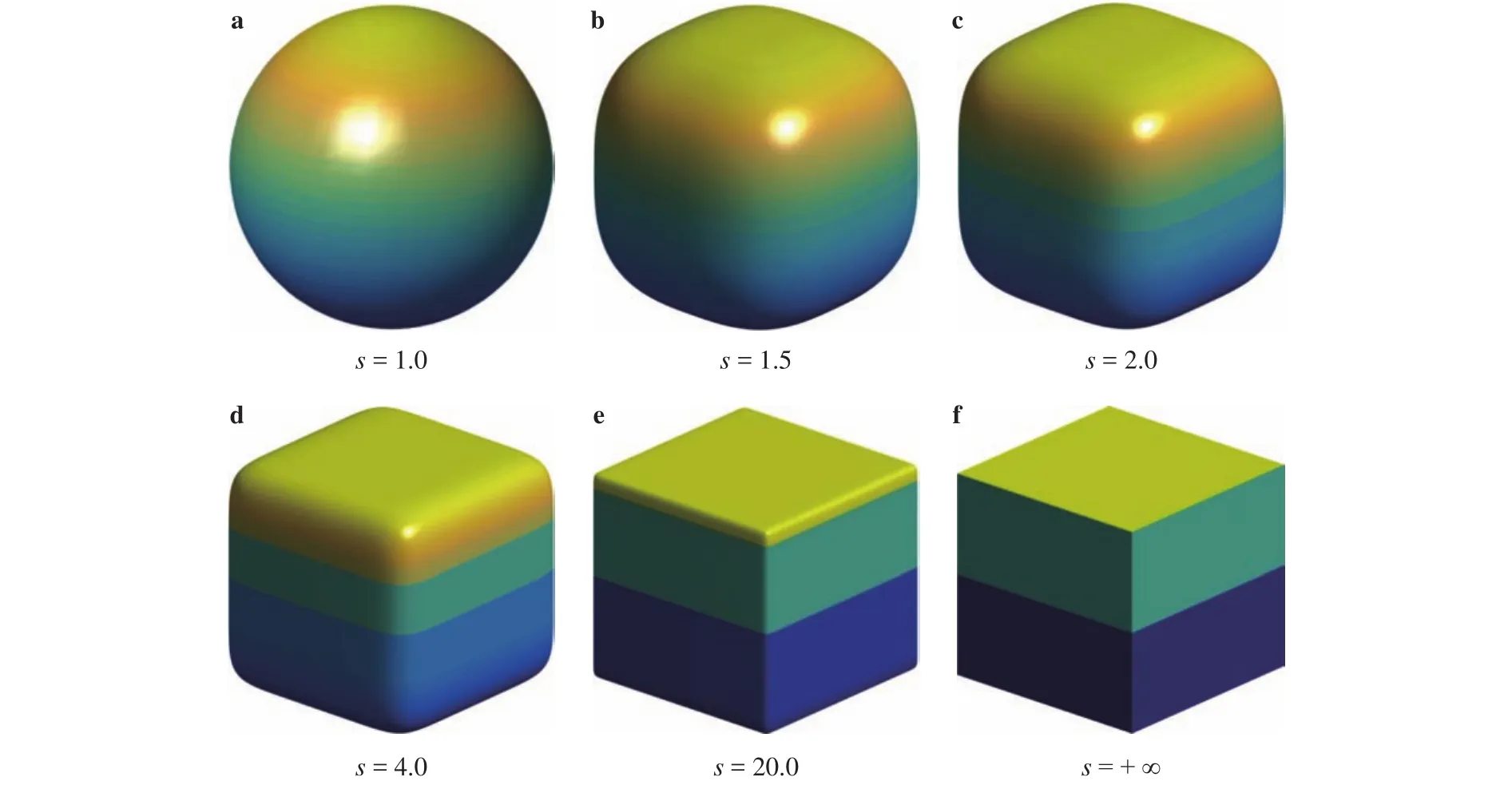
Fig. 1. Illustration of the surface of the cube-like particles with different s.
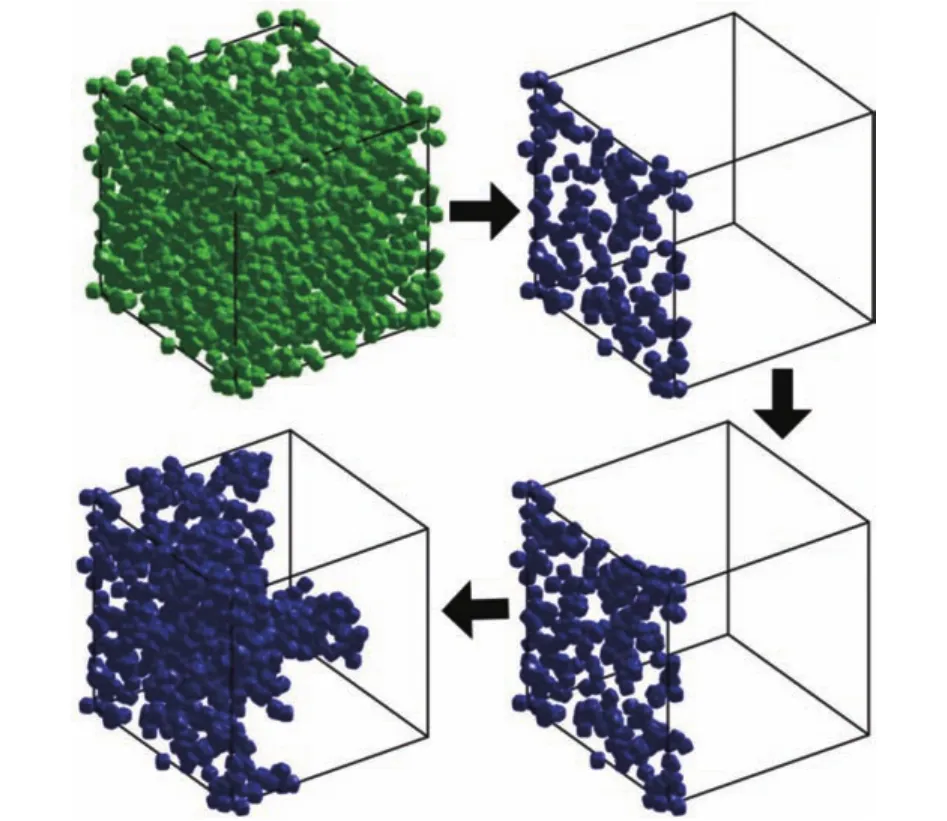
Fig. 2. Graphical presentation of one connected percolation cluster formed by the overlapping cube-like particles.
In the continuum percolation models, there exists a scaling relationship between the percolation probabilityPand the global percolation thresholdc. In this study, a commonly finite-size scaling technique [5, 11, 19] is used to derive the value ofcas below. Firstly, based on the cube-like particle percolation models, we obtained by above-mentioned method, the curves ofP(Vp,L)–Vpin finite-size systems for different shape parametersand container lengthLare drawn. Then, an adjusted Gauss error function is employed to obtain the fitting curves ofP–Vpas
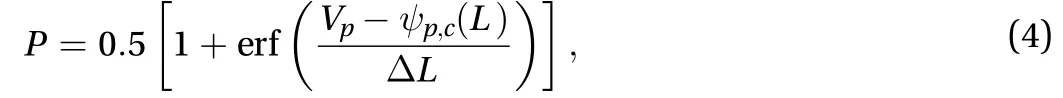
Based on the scaling relationship betweenLandL,, we can derive the correlation length exponentv.
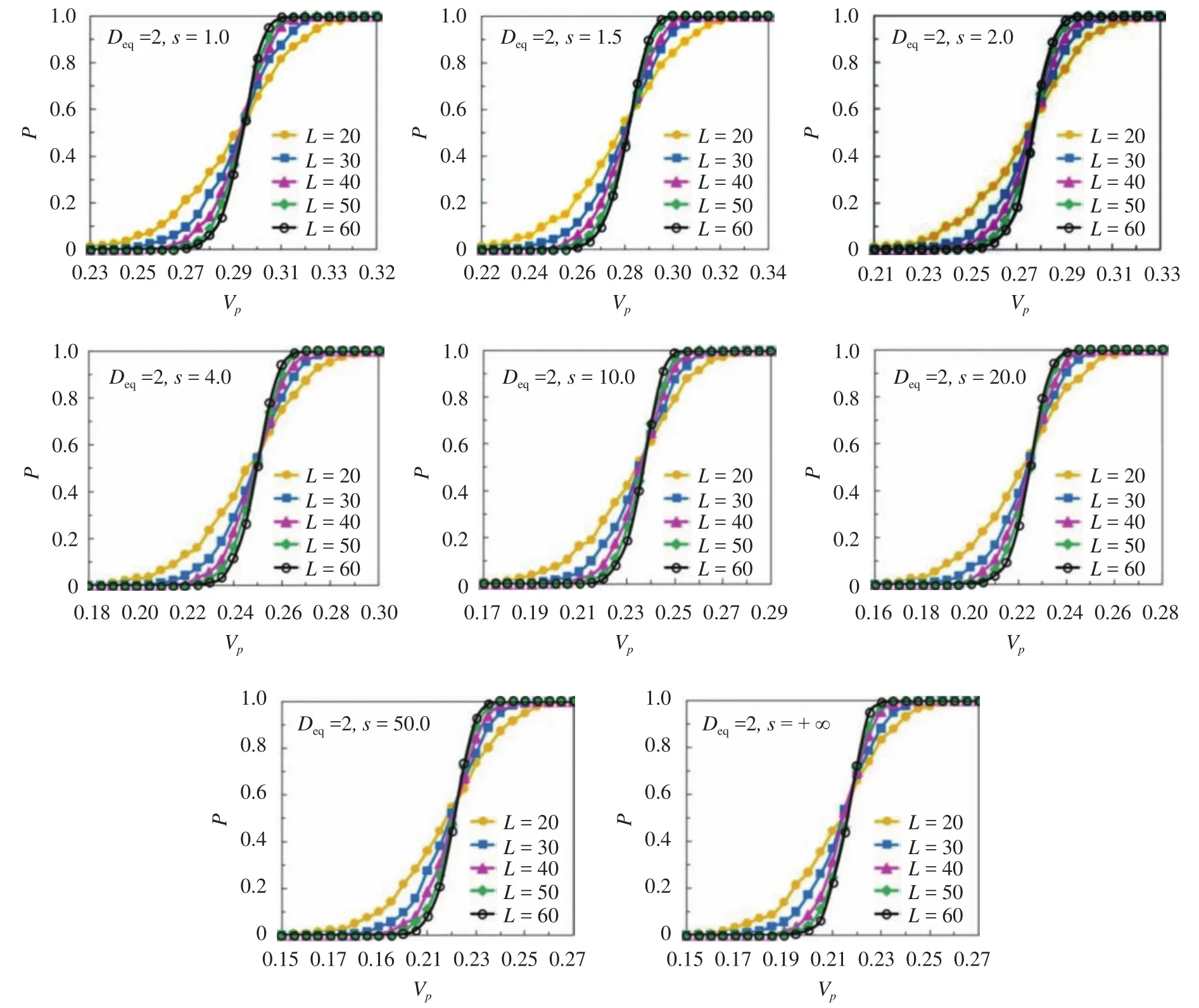
Fig. 3. Percolation probability P vs. Vp for different s and L.
As shown in Fig. 3, we present a series of the curves ofP–Vpfor cube-like particle percolation models withs= 1.0, 1.5, 2.0, 4.0,10.0, 20.0, 50.0, and, respectively. In all the models, the equivalent diameterDeq, which is the diameter of a spherical particle having the same volume as the non-spherical particle[20-22], is used to characterize the size of cube-like particles, and its value is equal to 2.0. For each of the percolation systems with the specifiedsandL, the number of the generated samples is fixed to be 2000. It is easy to find that for all of the obtainedP–Vpcurves, along with the increase ofVp, the percolation probabilityPwill increase. Meanwhile, all of the curves are very similar to the error function as Eq. (4). Besides, for the percolation models with the samesin Fig. 3, as the ratio ofLtoDeqincreases, the curves ofP–Vpwill become steeper, and the maximum curve slope will also be larger. For arbitrary cube-like particle systems,as the parametersincreases from 1.0 to +∞, the positions of the corresponding curves ofP–Vpalong with the sameLmove forward in the direction of the decreasing values ofVp, but, the shapes of theseP–Vpcurves almost keep unchanged here.
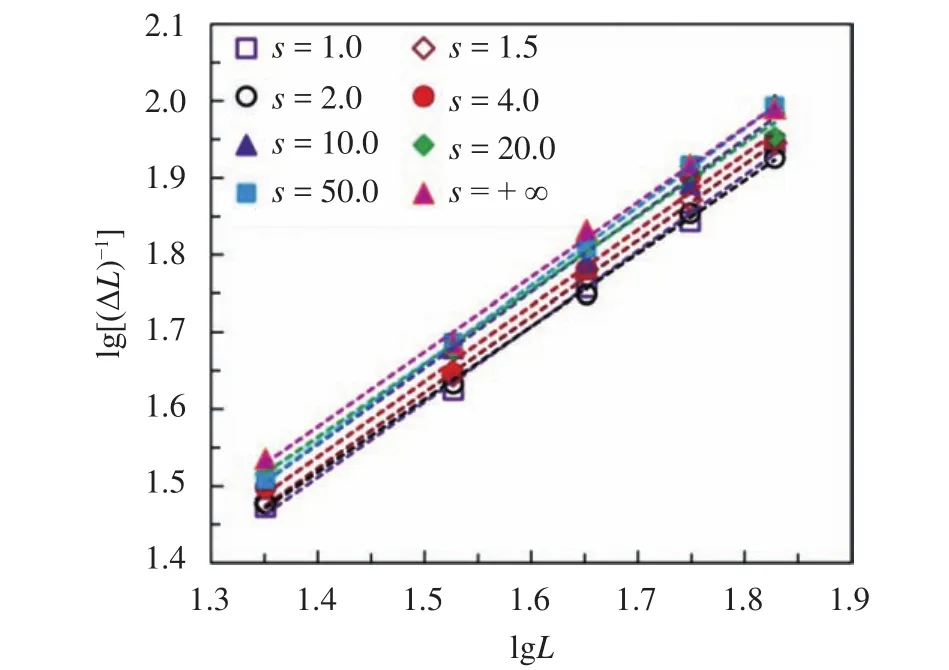
Fig. 4. Curves of lg[–1]–lgL for different shape parameter s.
Figure 5 displays the fitting curves offor the congruent cube-like particle percolation models with differents.And the crossing points of the fitting line ofwith thein Fig. 5 are equivalent to the global percolation threshold. In Table 1, the detailed values ofwithsbetween 1.0 andare listed. Takings= 1.0 (i.e., sphere) as an example,the global threshold= 0.2896 for cube-like particle is computed by using a linear fit to the corresponding points in Fig. 5.This value is close to the results reported in Refs. [4-6], which indicates the validity of the adopted methodology as well as the numerical results in present letter.
Figure 6 further shows the dependence of derived percolation thresholdof infinite-size systems composed of congruent overlapping cube-like particles on the shape parameters. It can be seen from Fig. 6 that whensis lower than 100.0, the value ofdramatically decreases with the increasingsfrom 1.0 to 100.0. Yet asscontinues to increase from 100.0, the decreased trend ofis gradually slowed down and finally the thresholdturns to be a stable value. From the study, we can know that only when the surface of all the cube-like particles is spherical (i.e.,s= 1.0), the obtained percolation thresholdis the maximum.This conclusion is basically consistent with the numerical res-ults for congruent ellipsoids [5] and spherocylinders [6].
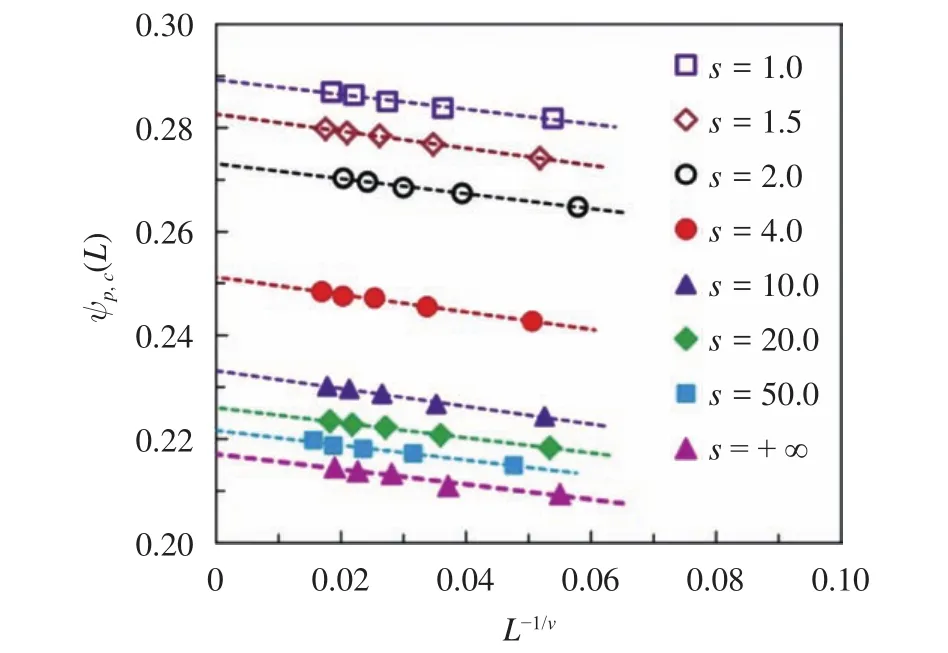
Fig. 5. Fitting curves of for different shape parameter s.
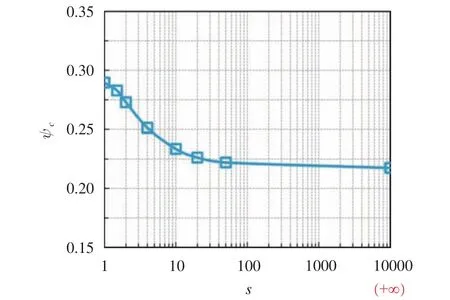
Fig. 6. Variation trend of with the increasing s from 1.0 to
Table 1 Derived global percolation threshold of cube-like particles in this study.

Table 1 Derived global percolation threshold of cube-like particles in this study.
?
Based on the geometrical model of cube-like particles and Monte Carlo method, the pore configuration in porous medium is considered to be the overlapping cube-like particles in the periodic cubic domain in this paper. By combining the particle packing models and the finite-size scaling technique, the influence of the cube-like particle characteristics on the global percolation threshold of particle systems is studied in detail. From the findings of this letter, the following conclusions are summarized. For the cube-like particles, as the shape parametersincreases from 1.0 to +∞: ① the positions of the curves of percolation probability vs volume fraction (i.e.,P–Vp) move forward in the direction of decreasing volume fractionVp. But, the shapes of theP–Vpcurves almost keep unchanged at the sameL; ② the percolation thresholdcdramatically reduces withsin[1.0, 100.0], and then the changing trend is slowed down gradually and finally turns to be stable. When the surface of cube-like particles is cubical and spherical, respectively, the minimum and maximum thresholds (i.e.,c,min= 0.2714 andc,max=0.2896) are obtained.
Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grants 51878152 and 51461135001) and the Ministry of Science and Technology of China “973 Project” (Grant 2015CB655102).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Traffic flow and safety analysis
- Air entrainment in a vertical dropshaft with limited air supply
- Intrinsic relationship of vorticity between modes A and B in the wake of a bluff body
- An improved lattice Boltzmann model for high gas and liquid density ratio in composite grids
- A visualized study of interfacial behavior of air–water two-phase flow in a rectangular Venturi channel
- Inlet flow disturbance effects on direct numerical simulation of incompressible round jet at Reynolds number 2500
