Traffic flow and safety analysis

Jing Go, Lili Di, Xu Gn

a The College of Post and Telecommunication of WIT, Wuhan 430073, China

b The Engineering Quality Supervision Bureau of Hubei Transport Department, Wuhan 430000, China

c Wuhan University, Wuhan 430072, China

Keywords:Traffic flow Cellular automata Safety evaluation

A B S T R A C T Traffic rule is a key factor affecting traffic flow and safety. We develop our models, including the cellular automata traffic flow model as well as the linear regression one, aiming at calculating traffic flow and evaluating safety conditions with varied traffic rules. Then, we thoroughly investigate four types of paths in a freeway, namely two straight lanes, three straight lanes, ramps,and roundabouts as case studies and discuss the different traffic rules as comparison. The results demonstrate that “Keep-Right-Except-To-Pass” rule is not as effective as the free rule in promoting traffic flow; however, this rule ensures safety for drivers better than the free rule. Additionally, a new traffic rule, which sets different posted speed limits for adjacent lanes, is proposed to promote better traffic flow with safety requirements satisfied. Furthermore, we apply effective rules and alternatives, left driving norms as well as intelligent system as extension and obtain better results.Finally, model’s sensitivity analysis regarding to probability of decelerating and posted speed limits proves the stability of our results.

Traffic rule is a key factor affecting traffic flow and safety in daily life, which also determines the pattern of traffic diagram. It is also a widely discussed topic by many researchers in the field of microscopic traffic flow. Thus, we develop our model aiming at generating an optimal situation for tradeoffs between traffic flow and safety according to the given rules, which is seldom discussed by the existing researches. The optimal situation contains two aspects, the maximum of traffic flow and the minimum of accidents. Considering the ambiguous statements, we make our own definition of some aspects in this problem firstly.We define the two-lane paths, three-lane paths, roundabout and ramps to eliminate the complexity of real condition of freeways.In the process, we establish an advanced model, which cover all these conditions as well as lane-changing, and an accurate model to quantify safety.

Nagel and Schreckenberg [1] proposed a classic cellular automata model under four rules for traffic flow of a single lane in 1992. Simultaneously, the NaSch model laid the foundation of modeling in traffic flow. Then, different models of traffic flow in terms of the theory cellular automata (CA) have been proposed,such as the cruise control model [2], Takayasu-Takayasu (TT)model [3], the Benjamin-Jofnson-Hui (BJH) model [4], velocity effect (VE) model [5], velocity-dependent randomization (VDR)model [6], and Fukui-Ishibashi (FI) model [7-14]. However, the traffic flow in our daily life is generally composed of various types of vehicles with different desired speeds and moving in more than one lane. Then the multi-lane models are published allowing the simulation of lane change, such as the works from Refs. [15-19]. Multi-lane models are currently studied in depth because these are closer to what happens to the flow of traffic in reality. In our traffic flow model, we take two-lane and threelane as the baseline to discuss the problem respectively, which can be deduced to the general cases.

Hence, based on the classic NaSch model, we develop the traffic flow model considering the different traffic rules, lanechanging rules as well as the speed-limit rules for two-lane,three-lane, ramp and roundabout respectively. Case study on these conditions is of great significance for finding the tradeoffs between traffic flow and safety. Given the factors of safety, we establish the model to guarantee the minimum number of accidents. Then we discuss the effectiveness of this rule in promoting traffic flow and suggest alternative factors. Lastly, we generalize the discussion of former rule to the opposite rule and apply earlier analysis to the intelligent system. In the process, we improve the existing algorithm to simulate the lane-changing,which could prove out the rationality of our results. Up to now,the existing researches fail to analyze the tradeoffs between traffic rules and safety according to the given rules in various traffic patterns. Besides, majority researches put more weight on the traffic flow analyses and neglect the significance of safety in the traffic patterns. In this paper, we do the above work and fill the gap on the basis of cellular automata model.

We approach the problem by first mathematically analyzing the two major factors, traffic flow and safety, in lane-changing,and establish two major models to quantify these two factors and make tradeoffs between them. Here are the conventions and assumptions used in this paper. The following definitions and variables will be used in our discussion of the problem.

●Lis the number of cells in a 1-dimensinal array.

●dnstands for the distance between then-th vehicle and its front one. And we usedn,ffor the distance between then-th vehicle and its front one in adjacent lanes,dn,bfor the distance between then-th vehicle and its rear one in adjacent lanes.

●Cnstands for the lane which then-th vehicle is in.

●Kis a key parameter to measure safety condition, which records total numbers of such situations.

●SVis a speed variable coefficient to measure posted speed limits. We use anequation in the safety simulation model to calculate it.

●Frefers to the accident rate in the equation of safety simulation model.

In addition, we make the following assumptions about the problem to simplify analysis.

● The physical quantities in our simulation correspond to that in real traffic for an exact proportion. This is a vital assumption in our process of simulation and guarantees the validity of our simulation.

● The micro-level dynamics can reflect that in macro-level.Thus, the micro- interactions are of great significance and typical in modeling.

● We assume that the majority drivers are willing to the maximum speed, and the others choose the cruise control system. It leads to randomness in the problem.

● The freeways we discussed are flat. We ignored the rugged condition of freeways.

● We assume that the psychological factors of drivers have little influence on our model and we ignore these.

Given the advantages of CA in capturing the complexity of the real traffic adequately, we establish the following model to analyze the traffic flow. In order to eliminate the complexity of real traffic of freeways, we take four types of paths into consideration, i.e. two-lane paths, three-lane paths, ramps and roundabout. We manage to simulate traffic flow and accident rate(which we regard as an indicator reflecting safety condition) respectively using our models. Hence, we develop two types of models to solve this problem: for the one to simulate traffic flow,we set different traffic rules to obtain flow data and time-space evolution tracking curve for each vehicle; while we apply multiple regression analysis to fit accident rate under different circumstances in the other one.

The traffic flow model basically consists of two components,i.e. following and passing. And NasCh model is a well-reputed one among those traffic flow models; however, it is defined on a 1-dimensional array, which is so simplified that cannot cover most situations. Hence, we proposed an advanced model based on the existing NasCh one.

Primary procedures in the model could be executed in orders below:

STEP 1: Using advanced NasCh model to update position of each vehicle in its own lane

STEP 2: Using certain passing rules (like the given “keep-itright” rule) to move vehicles from one lane to others

STEP 3: Back to step 1

Updating vehicles’ positions

We consider a 1-dimensinal array ofLcells, and each cell represents 7.5 m in real world. And each cell could be empty or occupied by a vehicle, each vehicle posses a velocity that ranges from 0 to 8 (216 km·h–1). A “gap function” is determined as:

wherexistands for thei-th position of a vehicle in a certain lane,the “gap function” hence clearly calculates the number of empty cells between adjacent vehicles in a lane.

Four steps are taken to update each vehicle’s position in our advanced NasCh model:

wherevjirepresents the velocity ofi-th position vehicle in lanej;vmaxstand for the maximum velocity a vehicle can reach;Gap(i)jfor the value that functionGap(i) applied on thej-th lane;vp-minfor the posted minimum speed in a freeway;xjiandx’jifori-th position of a vehicle onj-th lane before and after updating positions respectively.

Lane-Changing Principles

Clearly, it is the principle for vehicles of changing lanes that really matters among different paths. We propose that a driver would like to change his lane to become faster for two reasons:one is that he had been blocked in current lane while the other that his safety could been guaranteed. After thoroughly viewing those requirements, we set corresponding principles under“Keep-Right-Except-To-Pass” rule and others.

Two-Lane-Changing Principle

Equation (2) presents the definition of a flag parameter deciding whether changing lanes or not:

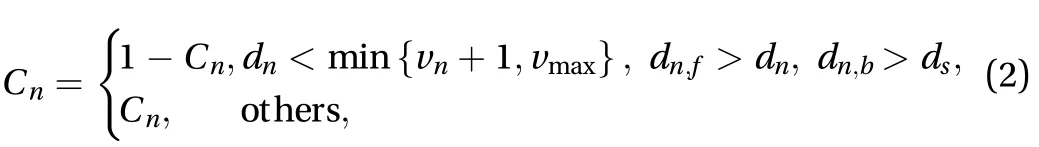
wheredsstands for the required safety distance of lane.

According to Eq. (2),dn＜min{vn+1,vmax} describes a situation that then-th vehicle is blocked in its current lane;dn, f＞dn,dn, b＞dsdescribes that this blocked vehicle could get faster in its adjacent lane without any safety threats.

Driving faster by changing lanes is not what decent driving actually means, driving faster with less safety threats is what we really care about. Hence, we introduce a key parameterKto measure safety condition. This parameter records total numbers of such situations:dn, b=ds, i.e. this car is seriously close to its rear one when lane is changed. Figure 1 shows the exact situation when lane-changing is possible, and satisfy constrains what Eq.(2) presents:

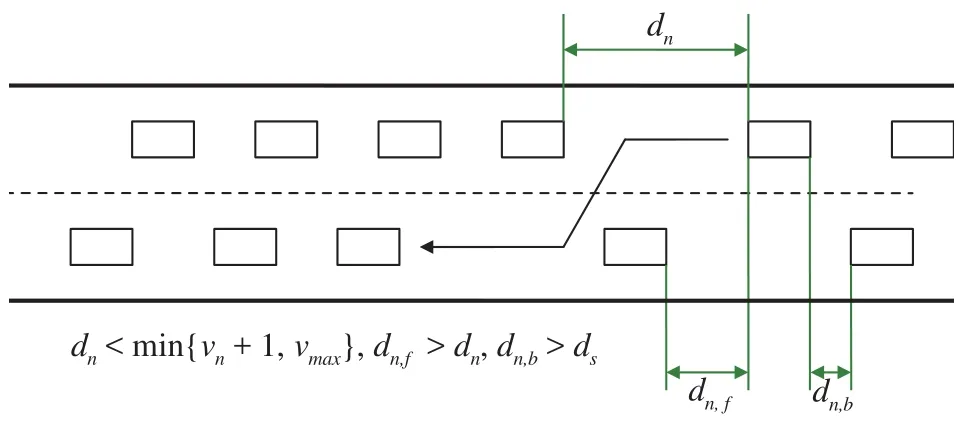
Fig. 1. Two-Lane-Changing diagram.

Multiple Lanes Changing Principles

Daoudia [18] has pointed out a basic three-lane-changing principle, we establish our own based on that. We mark lanes with 1, 2, …,Nlfrom right to left accordingly, and vehicles will change their lanes with following principle rules .

(1) Consider its right lane: ifthennew_ln(t) =lanen(t-1)-1 else,new_ln(t) =lanen(t-1).

(2) Consider its left lane: ifmin(vn(t)+1,vmax) orvn(t) = 0] and(t) thennew_ln(t) =lanen(t-1)+1

(3) Lane changing: letlanen(t) =new_ln(t) with probability (1-pignore). Apply this rule from right lane to left accordingly in case of collisions.

Rule (1) shows that vehicles preferred changing to their right lanes if their driving condition will not be bothered. Rule (2)shows that vehicles change to their left lanes only when left ones are better than their current lanes and right lanes. Besides,vn(t)=0 ensures that vehicle will not get stuck in traffic jam if they wish to change their current lanes. Rule (3) introduce a probabilitypignoreto describe a situation that drivers will not change their lanes even lane-changing requirements are satisfied.

Then we discuss the safety simulation model.

By safety evaluation, we mainly use accident rate to measure it. In our consideration, posted speed limit is a major factor influencing safety condition in freeways. Liu’s work [20] indicates that accident rate is related to traffic flow, average speed and posted speed limits, and it could be predicted by linear regression. However, this model is complicated in its form, we simplify it into solving this problem.

We introduce a speed variable coefficientSvto measure posted speed limits. Equation (3) gives the calculation ofSv

wherevais average speed during a period,is standard deviation ofvduring a given time Δt, and Δtis time period we pick up.

Clearly, in this equation,Svis in terms ofandva, which are strongly related to posted speed limits. In other words, higher posted speed limits ensure a higher average speed; moreover, it also encourages more vehicles to change lanes to obtain higher velocity. Hence,andvavary with the posted speed limits respectively thus causingSvvary with the posted speed limits.

We have Eq. (4) to estimate accident rate:

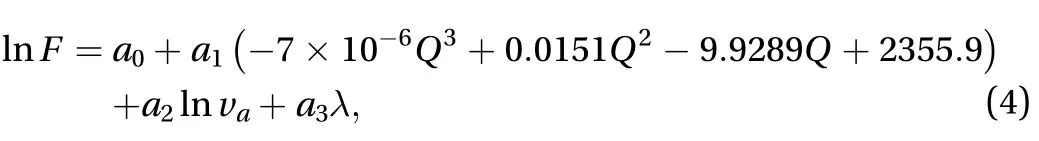
whereFis accident rate,ai(i=0, 1, 2, 3) is undetermined coefficient,Qis traffic flow during given time Δt,vais average speed during given time Δt, andis value of correspondingSv,see Table 1.

Before solving this equation, we have to do some simple transformation. Lety=ln(F),x1=ln(-7×10-6Q3+0.0151Q2-9.9289Q+2355.9),x2=lnva, thus turning Eq. (4) into a pure linear regression form as Equation (5) is the multiple linear regression equation to be solved in case studies.

Table 1 Value of.

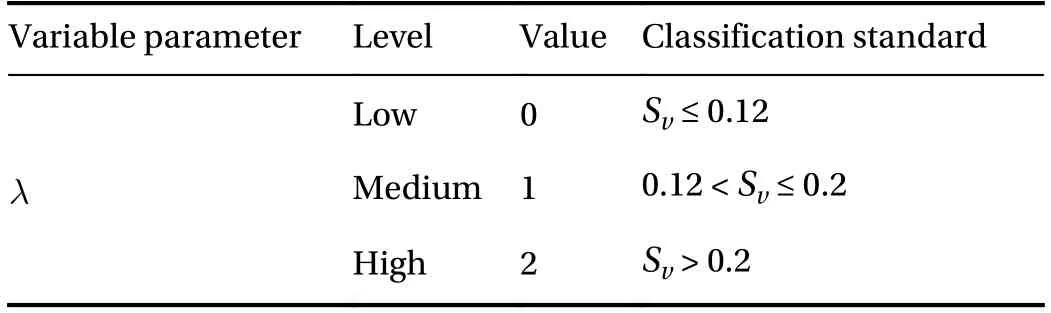
Table 1 Value of.

Low 0 Sv ≤ 0.12 Medium 1 0.12 ＜ Sv ≤ 0.2 High 2 Sv ＞ 0.2

For traffic flow, we would like to present our results with a“time-space” map besides regular statistics of traffic flow at each lane. By “time-space” map, we mean that a map records each vehicle’s position in terms of time. We create a 3-dimentional array.

Ai,j,k(0≤i≤ 599, 0≤j≤ 399, 0≤k≤ 2), and the first column of it is used for storing positions of each vehicle; the second column for storing time; the third column for storing RGB color. Once this array is accomplished, we load it into a BMP file that we have created before, thus making those tracks of vehicles visible.

For accident rate, we use Eq. (5) to calculate. Since there are 4 parameters in Eq. (5) to be solved, at least 4 sets of (F,Q,W)data are required. In facts, we get far more sets of (F,Q,W) data than we need. After ignoring some usefulness data sets, we plug some data sets into Eq. (5) to do linear regression.

Here follows an authentic example we calculate, and our results about accident rate are all gained by this method unless specially acknowledged.

In an example, we plug data sets into Eq. (5), and we get values of parameters as follows:

Table 2 Regression Parameters.

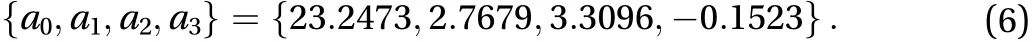
Before we plug these into Eq. (4), we have to check its regression parameters. Table 2 shows those parameters.

By checking these parameters in related statistical tables, we are confirmed that the regression makes sense; hence, we could plug Eq. (6) into Eq. (4), and we obtain an analytic expression ofF.

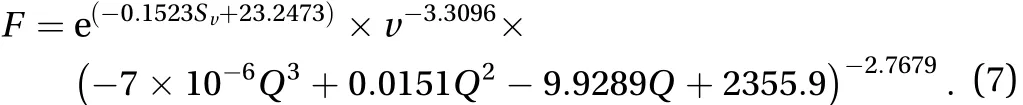
According to this analytic expression, we could plot the graphic ofFin terms withvandQ, and see the trend of accident rate whenvandQvary.

(1) Two/Three-Straight-Lane Case

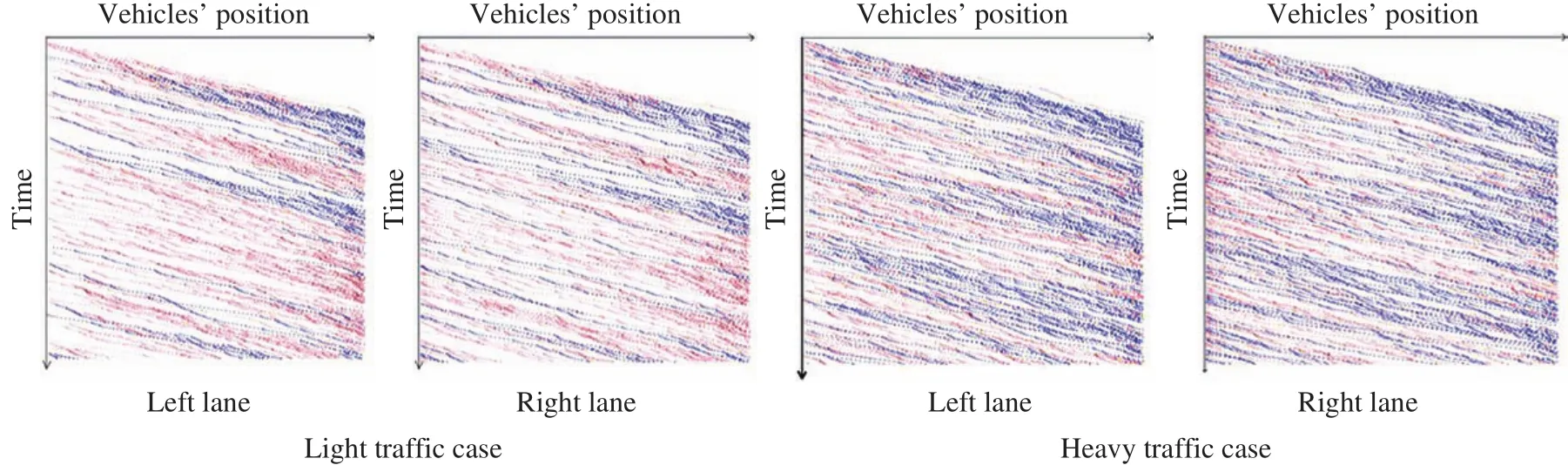
Fig. 2. Time-space graphic in two-straight-lane under light and heavy traffic.

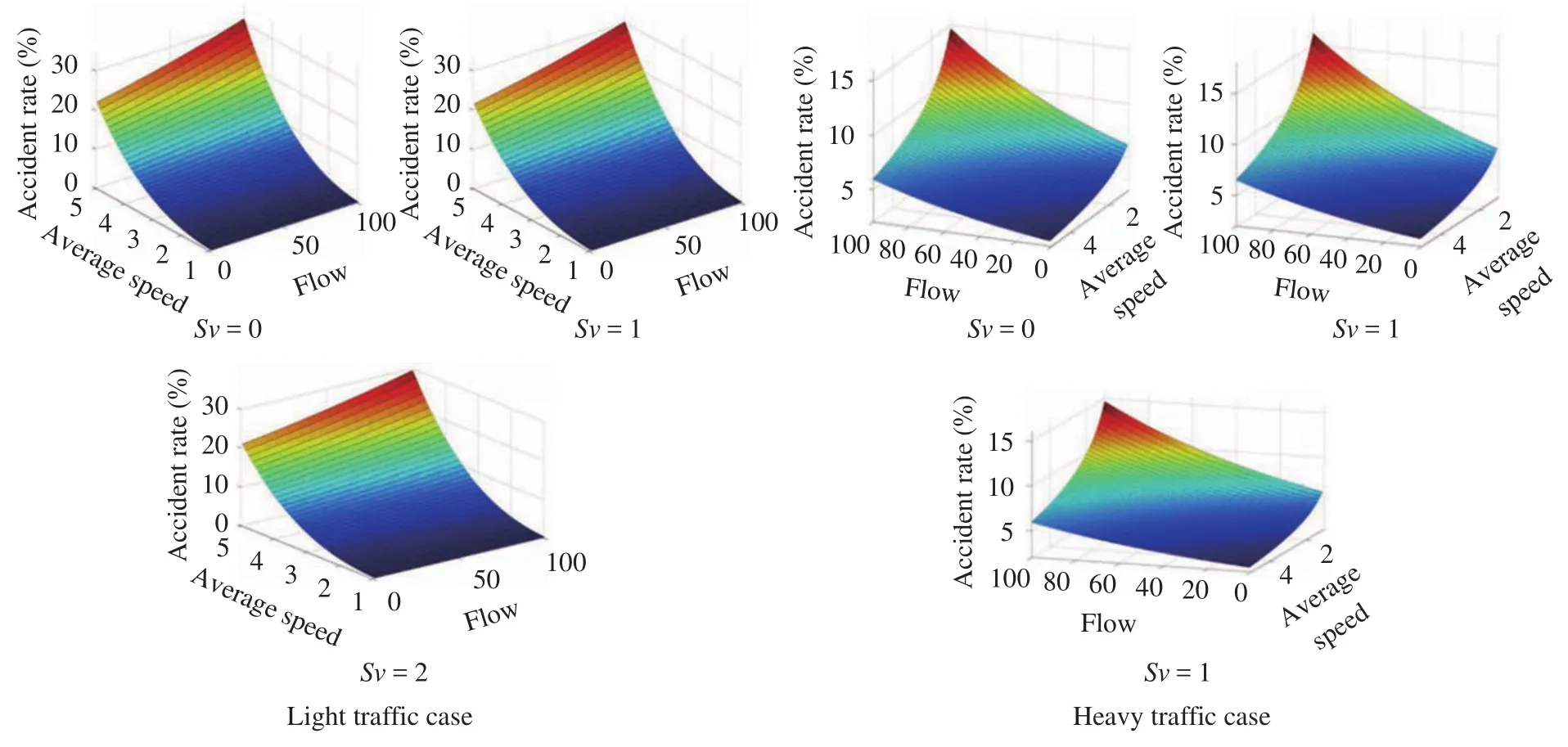
Fig. 3. Prediction of accident rate in terms with traffic flow and average speed.

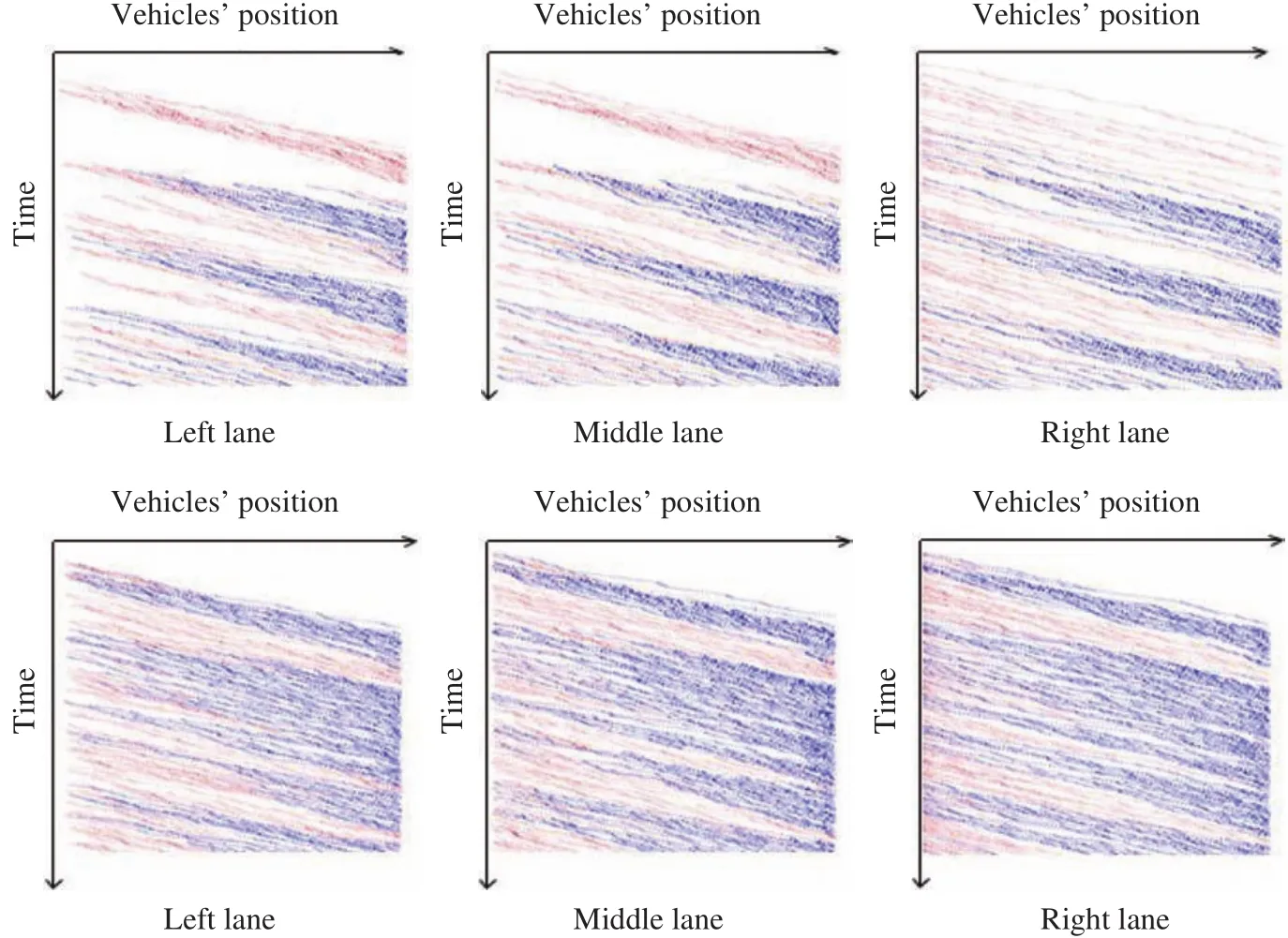
Fig. 4. Time-space graphic in three-straight-lane. The three graphs on the top are in light traffic case, the other three on the bottom are in heavy traffic case.

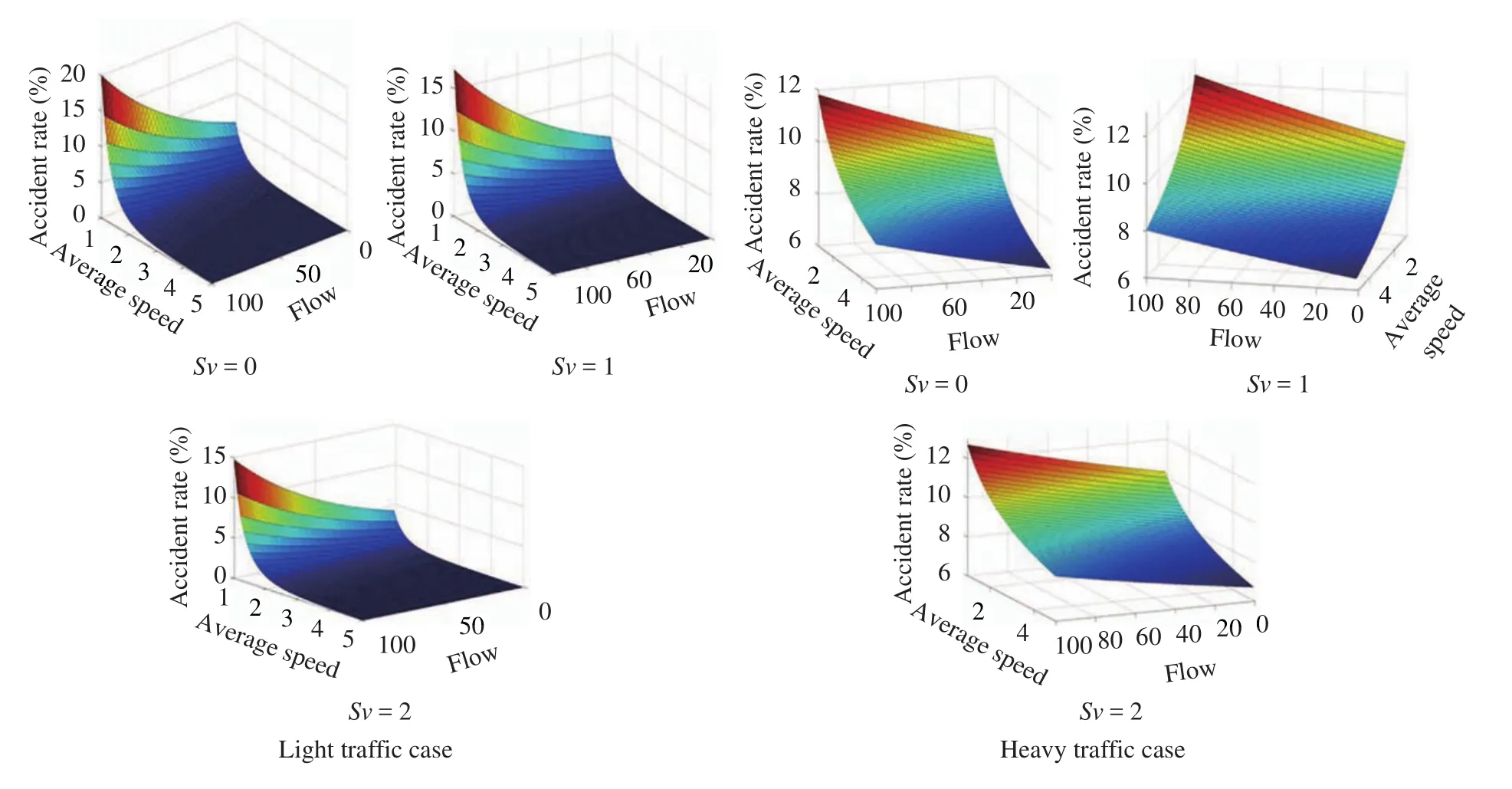
Fig. 5. Prediction of accident rate in terms with traffic flow and average speed.

In this case study, we apply Eq. (2) as lane-changing rules for vehicles, and Eq. (1) as updating rules for each lane respectively.Previous works [20, 21] have pointed out that vehicles are nearly Poisson distributed when traffic is light while binomial distributed when traffic is heavy. And we have set a “button” in our Matlab code to distinguish “light traffic” and “heavy traffic”;hence, our results will be presented under these circumstances.

Figure 2 is a time-space graphic which reflects each vehicle’s position in terms of time in two different conditions, which are light traffic case as well as the heavy traffic one for two-straightlane case. Figure 3 describes accident rate under different value ofλ, i.e. different posted speed limits.

Accordingly, Fig. 4 is a time-space graphic which reflects each vehicle’s position in terms of time for three-straight-lane case. Figure 5 describes accident rate under different value ofλ,i.e. different posted speed limits.

Finally, Fig. 6 compares arrival flow under these two traffic loads, namely light traffic and heavy traffic, in the above two cases.

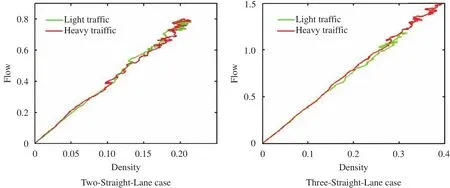
Fig. 6. Comparison of arrival flow under two traffic loads in different cases.

(2)Ramp Case

Ramps are common paths in most freeways, and Fig. 7 shows how it works.

In this figure, vehicles enter laneAfrom rampB, and leave the freeway from rampC. Our models can not directly be applied in ramps, however, we can regard the process that vehicles entering laneAfrom rampBas a simple lane-changing process with only one direction to choose from. Hence, Eq. (2) could be applied here. And we assume a probabilitypexitto leave laneAfrom rampCfor vehicles passing through this exiting ramp. Besides, lane-changing rule betweenAandEis in agreement with our previous model, i.e. Eq. (2).

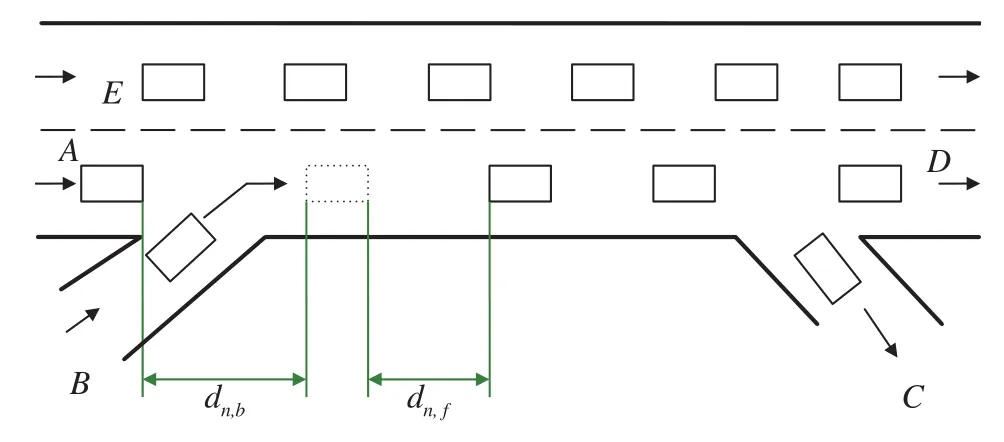
Fig. 7. Ramps Diagram.

Figure 8 shows time-space relationship for each vehicle in laneAand laneE. Figure 9 shows traffic flow in rampBand rampC, while Fig.10 demonstrates traffic flow in laneAand laneE.

Fig. 8. Time-space graphic in two-straight-lane under different traffic.

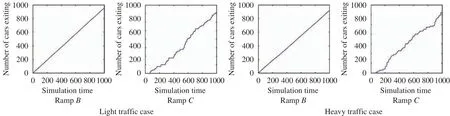
Fig. 9. Traffic flow in ramp B and ramp C.

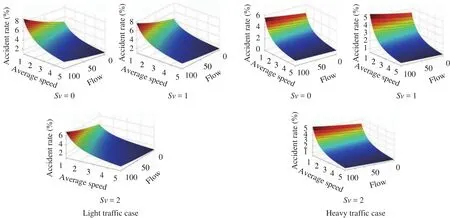
Fig. 10. Prediction of accident rate in terms with traffic flow and average speed.

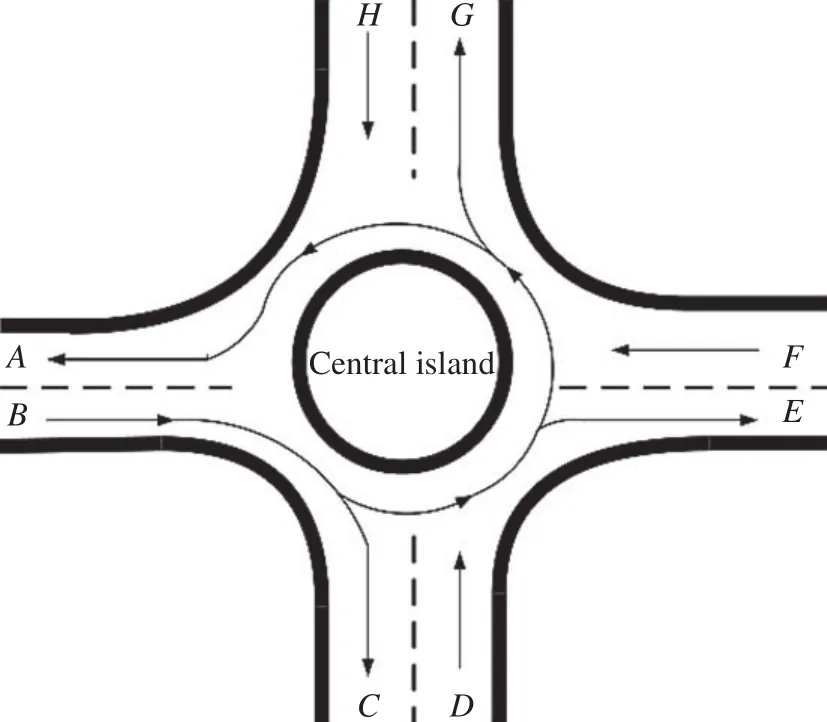
Fig. 11. Roundabout.

(3)Roundabout Case

A roundabout is also named “traffic island” which functions as guiding vehicles at different steering. Figure 11 demonstrates how a roundabout works.

In this roundabout, vehicles could drive into it throughB,D,F, andH; and they could leave it throughA,G,E, andC.

We set 4 basic rules for every vehicle in this roundabout:

(1) Each vehicle may drive into this roundabout in one of four entrances of it with probabilitype=0.25

(2) Each vehicle may leave this roundabout in one of four exits of it with probabilitypo=0.25

(3) Central Island could not be passed through

(4) Every vehicle should circle around this roundabout counterclockwise, and it may leave at any of the four exits

We build our algorithm based on these rules; brief procedures of our algorithm are listed as follows:

● Check each entrance whether there is a chance to generate a vehicle (i.e. enough safe space)

● Update new vehicles with certain probability in each entrance, count the total number of vehicles input

● Analyze every vehicle’s speed and position; let those leave this roundabout with certain probability when they drive near any exit; and count the total number of vehicle output

● For those vehicles in the ring road of this roundabout, use our previous model to update their speed and position.

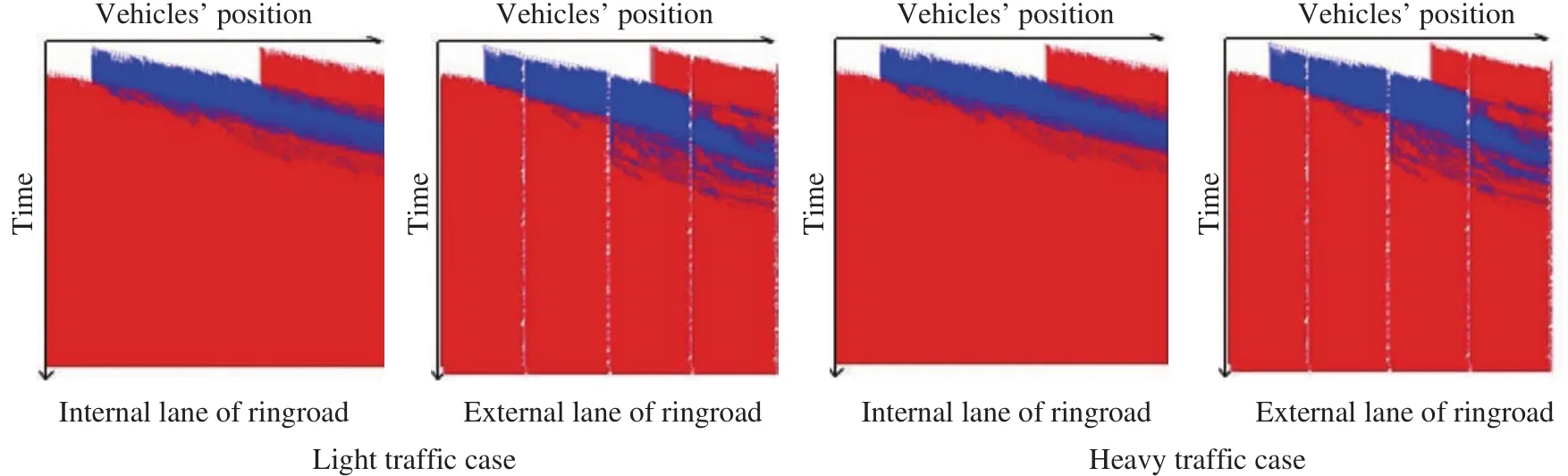
Fig. 12. Time-space graphic under different traffic.

Figure 12 shows time-space relationship for each vehicle in internal lane and external lane of ring road near the center island. Figure 13 describes accident rate under different value ofλ, i.e. different posted speed limits.

Based on the above ramp case and roundabout case, Fig. 14 compares arrival flow under light and heavy traffic loads.

Moreover, there are some extensions of the above model and we would discuss it in the following three aspects, namely the alternative rules, different driving norms and the intelligent system.

To check whether this “Keep-Right-Except-To-Pass” rule is effective in promoting traffic flow, we firstly carry on several simulations with and without this rule respectively. We choose twostraight-lane as our simulation environment.

The left graph of Fig.15 demonstrates that the “Keep-Right-Except-To-Pass” rule could not promote traffic flow as much as the free rules.

Figure 16 shows that, however, this “Keep-Right-Except-To-Pass” rule is relatively safer than free rules.

The alternative we proposed is limiting the speed of different lanes. We take two-lane freeway for example to state it. The lowest speed of the quick lane should be determined over the highest speed of slow lane. Thus, the vehicles must slow down when returning to the slow lane. And this solution can reduce the lane-changing behaviors. Besides, making divisions in speed among different vehicles can reduce the accident rate and enhance the safety of traffic.

The graph on the right of Fig. 15 demonstrates that alternative could promote traffic flow as well as the safety factor.

Since our algorithm is flexible, we secondly change our initial conditions to obtain results of left driving norms. We choose a two-straight-lane to demonstrate this. In our algorithm, we only have to do a symmetry transformation of initial conditions.In other words, vehicles depart on the right lane while on the left lane if left driving rule is employed; and Eq. (2) only has to do a symmetry transformation to ensure vehicles passing from right lanes. We obtain our result as Fig. 17.

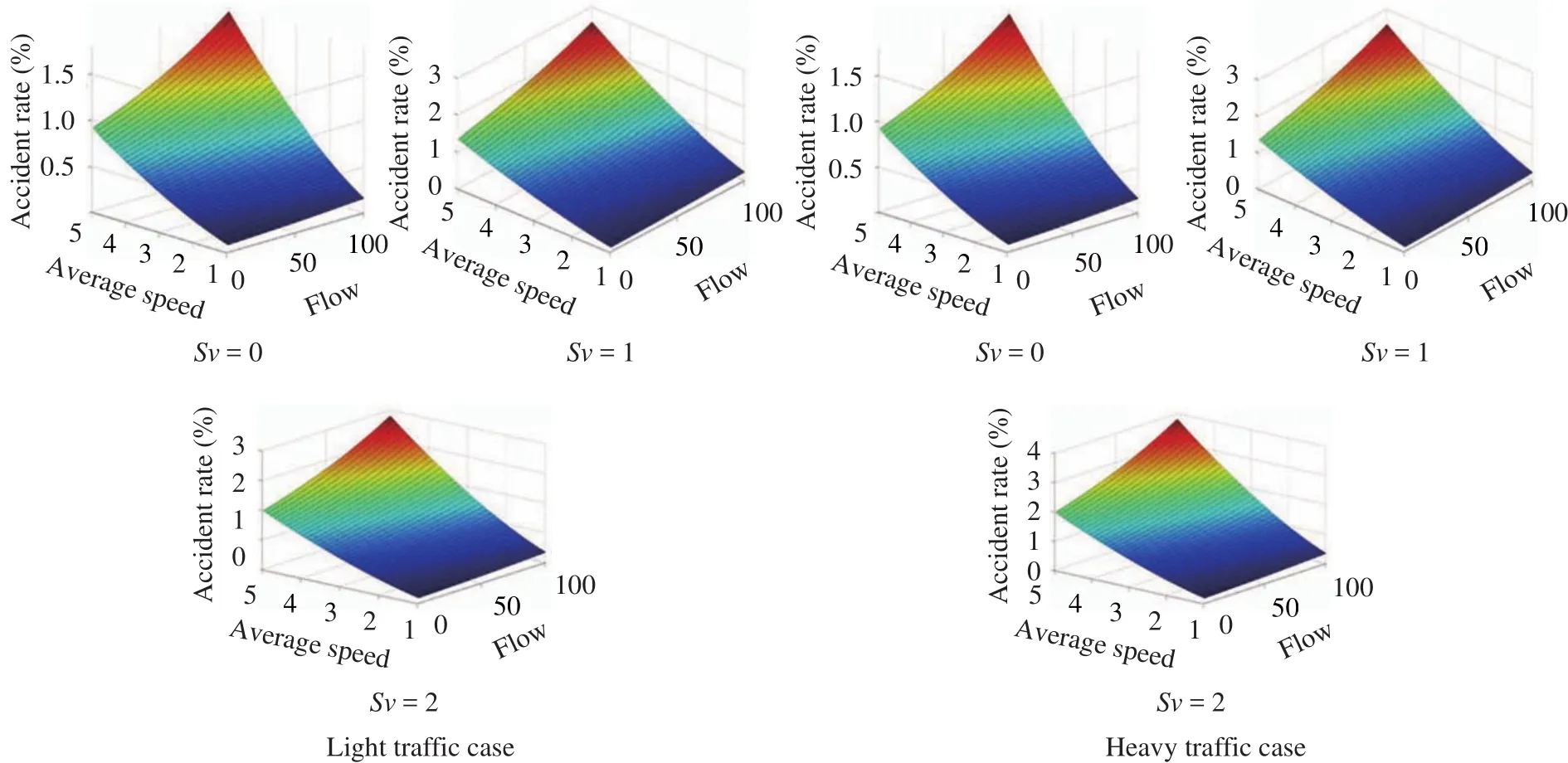
Fig. 13. Prediction of accident rate in terms with traffic flow and average speed.

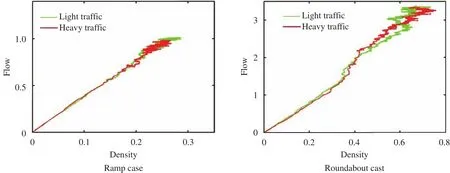
Fig. 14. Comparison of arrival flow under two traffic loads in different cases.

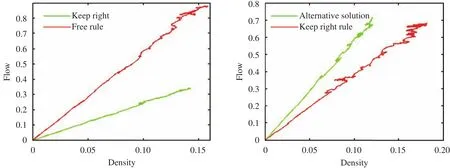
Fig. 15. Flow comparison.

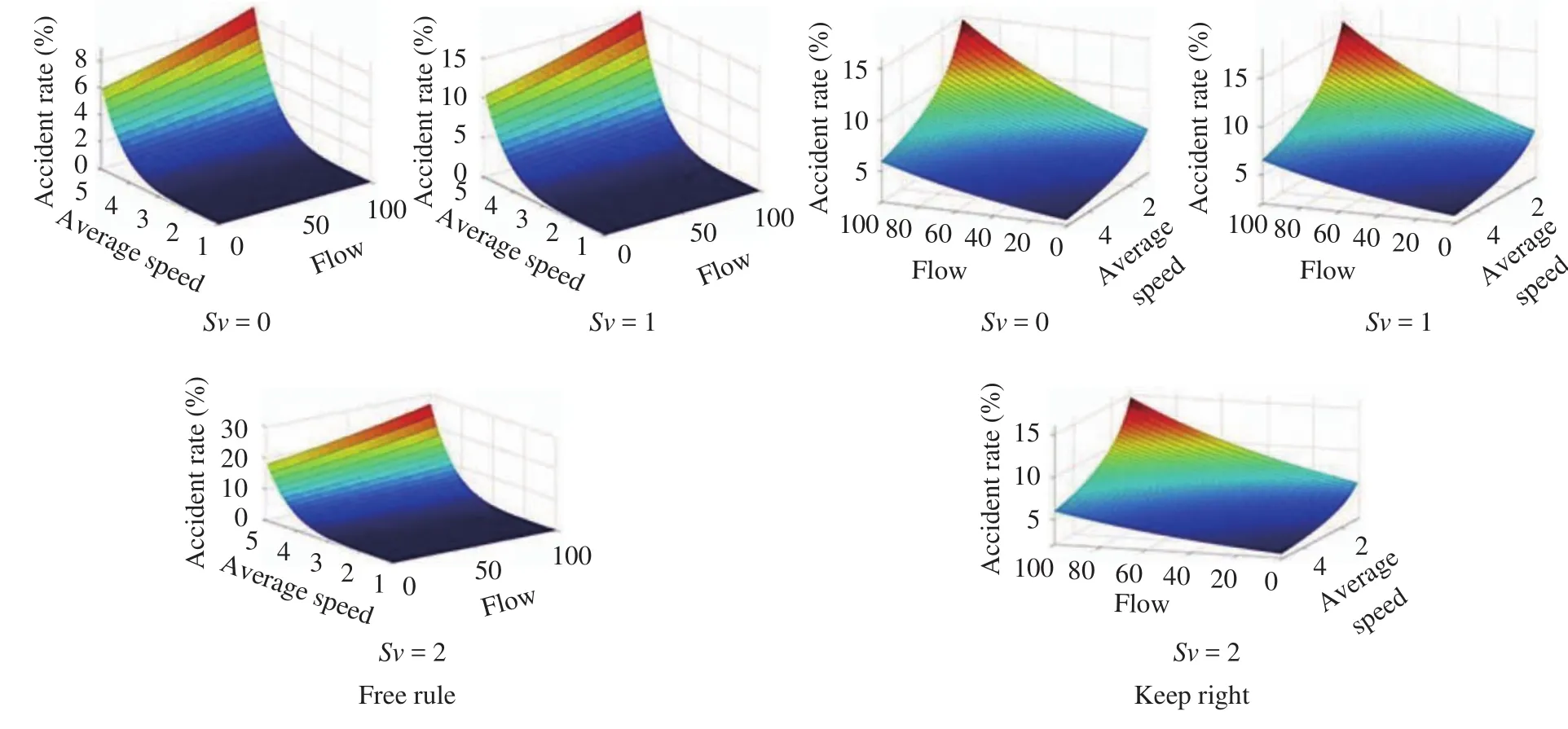
Fig. 16. Accident rate comparisons.

Thirdly, in intelligent system, we ignore the random factors,such as the emotions and behaviors of drivers. Thus, we can’t apply the initial model for intelligent system.

We put off the random factors to cover this condition and simulate under rigorous logic.

The following changes are applied in our simulation.

● Ignore the procedure of random slowing down in initial algorithm.

● In our former model, we set an exact probability for divers to change lanes when they meet the requirements of lane-changing. In intelligent system, we ignore the probability and drivers can determine whether to return to the primary lane after lanechanging.

Figure 18 shows the intelligent system for opposite traffic flow conditions as well as the accident rate, the left one represents the heavy traffic and the right one for the light traffic.

Moreover, we conduct this sensitivity analysis by changing values of some parameters in the model.

● Maximum Speed Limit

We change the maximum speed limit to 5, 8, and 11. Traffic flow and accident rate are recalculated respectively with each speed as delineated in Fig.19.

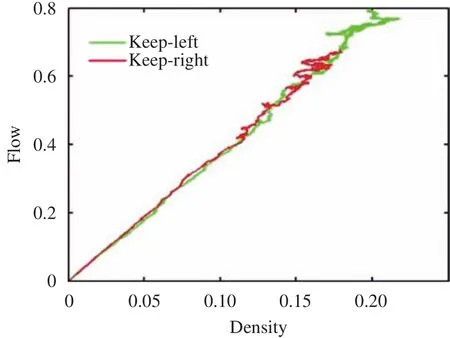
Fig. 17. Comparison between two rules in terms with traffic flow.

From the left graph in Fig. 19, it shows that Accident Rate does change a little associated with maximum speed. The right graph above shows clearly that the traffic flow does not change too much even when maximum speed varies largely.

● Probability of deceleration

We change the probability of deceleration to examine the accident rate and traffic flow. The given three probabilities, that are 0.1, 0.2, and 0.3, have different accident rates as well as traffic flow. It can be clearly drawn from Fig. 20.

Figure 20 demonstrates that flow fluctuates whenP,the probability of random deceleration, varies slightly. Obviously,this model is very sensitive to the change ofP; however,Pis almost fixed in real world. Hence this parameter will not affect the model as we may expect. Thus, analysis in this section proves our model relatively stable.

In conclusion, based on the NasCh rules, we develop a cellular automata traffic flow model and a linear regression model to calculate traffic flow and evaluate safety conditions respectively.In addition, we investigate four types of paths in a freeway,namely two straight lanes, three straight lanes, ramps, and roundabouts. In studies of these four cases, traffic flow, “timespace” map and safety condition are obtained under light and heavy traffic. Then we compare the “Keep-Right-Except-To-Pass” rule with the free rule in the two-straight-lane case. The results demonstrate that “Keep-Right-Except-To-Pass” rule is not as effective as the free rule in promoting traffic flow;however, this rule ensures safety for drivers better than the free rule. Additionally, a new traffic rule, which sets different posted speed limits for adjacent lanes, is proposed to promote better traffic flow with safety requirements satisfied. For left driving norms, our solution could be simply carried over with the substitution of two initial conditions, i.e. position for vehicles to depart and lane-changing rules. We establish an intelligent system ignoring the previous randomness of decelerating and lanechanging, under which both traffic flow and safety condition get better. Finally, model’s sensitivity analysis regarding to probability of decelerating and posted speed limits proves its stability.

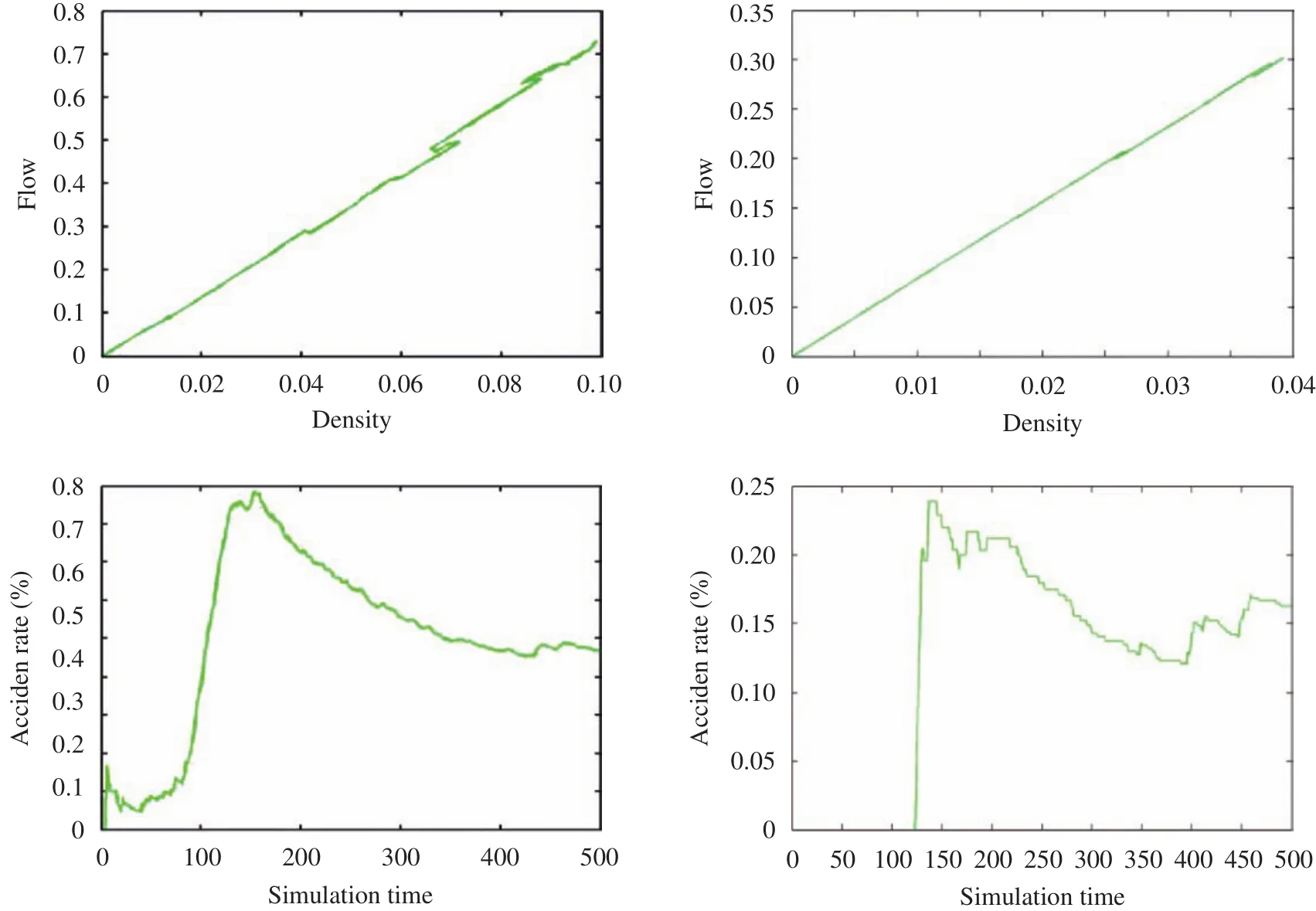
Fig. 18. Traffic flow conditions & Accident rate under intelligent system.

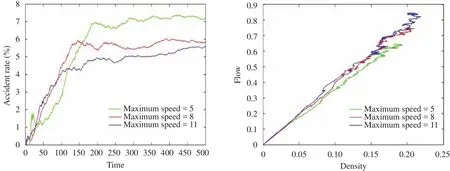
Fig. 19. Accident rate and flow comparisons under different speed limit.

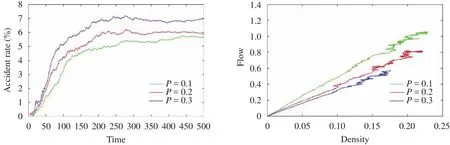
Fig. 20. Accident rate and flow comparisons under different probability.

Acknowledgements

Here we acknowledge the support of Wuhan Transport and Communications Committee (WHJT-CZH-2016-1C178).