基于群体Parrondo博弈的根分枝建模方法
2018-11-22李松阳高继勋刘晓东余文奇
李松阳,高继勋,王 淼,刘晓东,余文奇
(河南工程学院 计算机学院, 郑州 451191)(*通信作者电子邮箱lsy_cqu@cqu.edu.cn)
0 引言
根系是植物连接土壤与地上部分之间实现物质交换的重要桥梁,是植物吸收水分、养分资源和响应土壤环境变化的重要器官[1]。植物根系结构十分复杂,且埋藏在不透明介质中,难以观测,对根系进行定量化研究十分困难,因此建立根系结构模型,采用计算机模拟重现根发育过程是用于根系研究非常有用的工具。由于根系的分枝过程对根系生长发育有重要影响,其可塑性导致复杂根系的产生[2],因此在根系结构模型中,如何对根系的分枝过程建模是一个重要的问题。目前国外主流的根系三维结构模型包括RootMap、RootTyp、SimRoot、SpacSys和RootBox等[3]。在RootMap模型中,通过定义分枝密度,顶端不分枝持续时间或分枝延迟时间等参数实现对根系分枝过程的模拟[4-5]。在RootTyp模型中,通过定义分枝间隔控制根原基的产生,经过根原基的发育延迟时间后根原基发展为分枝[6]。在SimRoot模型中,通过定义经验的分枝频率以及生长角度实现对根系分枝过程的仿真[7]。在随后的OpenSimRoot模型中,依然通过参数分枝频率对根系分枝进行建模[8]。在SpacSys模型中,通过参数分枝位置实现对根系分枝过程的仿真,其中分枝位置由顶端不分枝长度、基端不分枝长度以及分枝间隔所决定[9]。在RootBox以及随后的CRootBox模型中,通过预定义分枝距离、分枝数目、顶端不分枝长度,以及基端不分枝长度等从参数决定根系分枝产生的位置[10-11]。在国内,张吴平等[12]定义了一个表征根个体周期性生长发育的基本单元(根元)。当根元的生长年龄大于1时,根元上的侧根原基可以发育形成分枝。金明现等[13]依据参数距顶端长度实现侧根位置的模拟。通过以上描述可以看出,现有的国内外主流根系结构模型中认为根分枝过程具有向顶的趋势,是一个向顶序列,并且没有考虑根原基对根分枝的作用。虽然根原基是顺序出现的,是一个向顶序列。但根原基发展成为根分枝是一个受到环境以及根原基本身影响的可调制过程,并不完全是顺序的。研究表明,虽然根原基的产生具有向顶序列的特性,但根原基发展为侧根的过程并不是一个严格的向顶序列[14]。为了弥补上述方法的不足,充分考虑环境以及根原基对根分枝形成的影响,本文提出一种基于群体Parrondo博弈的根分枝仿真方法,用于异质根系生长环境下根分枝可塑性建模。该方法通过构建根原基为个体的根原基群体,采用Parrondo博弈实现根原基群体间的交互,依据群体交互结果,实现根原基个体中生长素更新,从而对根分枝过程实现建模,为根系建模与仿真研究提供模型支撑和分析手段。
1 模型描述
Parrondo博弈认为:对于给定的两个博弈,如果每个博弈输的概率都大于赢的概率,那么当这两个博弈随机或周期进行时就可能产生一种获胜的结果。同时生物个体具有两重属性——种群属性和自然属性,种群(社会)属性决定了同种个体之间存在竞争合作关系,自然属性则揭示生存环境对个体存在的影响[15]。由于根系结构具有环境适应的特性,因此对于根系来说,各器官组织间的协调尤其重要。本文采用群体Parrondo博弈模型来模拟根系分枝过程,按照如下步骤进行:
步骤1 构建以根原基为个体的根原基群体。依据根自相似结构,划分根为顶端不分枝区域n_la,基端不分枝区域n_lb,以及分枝区域lb;随着根的伸长,当根长度大于顶端不分枝区n_la与基端不分枝区域n_lb长度之和时,依据根原基的序列产生方式及其发展窗口dw大小,对分枝区域lb进行顺序分割,则分割区域i即为第i个根原基rpi,分割区域i+1为根原基rpi+1,其中根原基rpi与根原基rpi+1为邻居根原基,最后,建立包含多个根原基个体rpi的根原基群体RS(如图1所示)。

图1 根原基群体示意图Fig. 1 Schematic diagram of root primordial swarm
步骤2 获取某个根原基个体rpi的邻居根原基集合。遍历根原基群体RS,对于其中的第i个根原基rpi,获取其邻居根原基集合rp_Neg={rpi-1,rpi+1}。如果rp_Neg不为空,遍历rp_Neg,对于其中的第j个根原基rpj,计算rpi与rpj的交互结果;如果rp_Neg为空,则rpi不与其他根原基交互。
步骤3 计算根原基个体rpi感知环境因素影响因子Ei及环境变化强度g。以根原基rpi为旋转轴,以r为旋转半径构建圆柱形区域,获取当前时刻t时该区域内的环境因素总量Ei_upt(t)。设定根原基rpi最小资源需求量Ei_min,最优资源需求量下限Ei_opt1,最优资源需求量上限Ei_opt2,最大资源需求量Ei_max,计算当前时刻t时环境因素影响因子Ei(t)(如式(1)所示)以及环境变化强度g(如式(2)所示)。
Ei(t)=
(1)
(2)
其中:h为显著性变化下限;Δt为生长间隔时间。
步骤4 采用Parrondo博弈模型计算rpi与rpj交互的输赢。rpi与rpj随机选择以概率p′=p-ε*Ei进行A博弈或者以概率1-p′进行B博弈,ε为斜率,其取值为正小数。如果进行A博弈,依据当前时刻t时rpi与rpj生长素含量Ci(t)和Cj(t),初始生长素含量Ci_0和Cj_0以及生长时间Ti和Tj,计算当前时刻t时rpi与rpj的生长素收益Wi(t)(如式(3)所示)和Wj(t)(如式(4)所示);计算当前时刻t时rpi相对于rpj赢的概率pij(如式(5)所示)。
Wi(t)=Ci(t)-Ci_0
(3)
Wj(t)=Cj(t)-Cj_0
(4)
(5)
如果进行B博弈,当在时刻t时rpi生长素含量Ci(t)能够被M整除时,计算环境影响的rpi赢的概率为p2′=p2-ε*Ei, 当在时刻t时rpi生长素含量Ci(t)不能够被M整除时,计算环境影响的rpi赢的概率为p3′=p3-ε*Ei。其中p2、p3分别为两种情况rpi赢的概率最大值。
步骤5 计算在时刻t+Δt时根原基rpi生长素含量和生长时间Ti(如式(6)所示)。如果进行A博弈,当rpi赢时,rpj支付a单位的生长素给根原基个体rpi;当rpi输时,rpi支付a单位的生长素给根原基个体rpj。如果进行B博弈,如果rpi赢时,rpi增加a单位的生长素;如果rpi输时,rpi减少a单位的生长素。设定根原基个体rpi博弈赢时符号sig=1,博弈输时符号sig=-1,及其在生长间隔Δt中固定收益b,则计算在时刻t+Δt的rpi生长素含量Ci(t+Δt)(如式(7)所示)。
Ti+Δt=Ti+Δt
(6)
Ci(t+Δt)=Ci(t)+sig*a+b;b>a
(7)
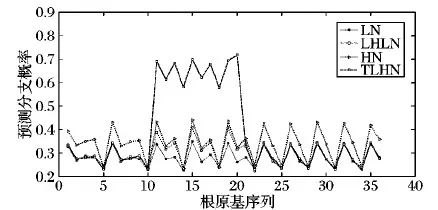
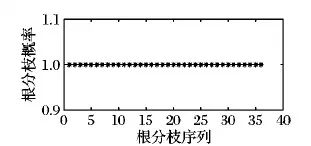
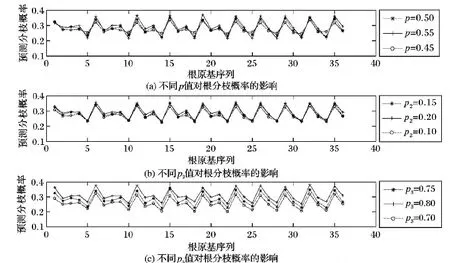
步骤6 根分枝预测。遍历根原基群体RS,对于其中的第i个根原基个体rpi,获取在时刻t时rpi生长素含量Ci(t)。设定rpi生长素需求最大值Ci_max及其发育时间Tlim。如果Ti 设定根系最大生长周期为20 d,根系依据生长函数(式(8))进行生长[11]。 λ(t)=k(1-exp(-(ρ/k)t)) (8) 其中:k为根最大长度;ρ为初始生长速度。当根长大于n_la与n_lb之和后,依据根原基发展窗口dw大小,按照向顶的方向顺序对lb区域进行分割,从而构建根原基个体,形成根原基群体,进而通过根原基群体Parrondo博弈实现根分枝仿真。设dw=0.4,n_la=1.57,n_lb=0.07,k=26.9,ρ=2。根原基环境感知半径r=0.01,最小资源需求量Ei_min=30,最优资源需求量下限Ei_opt1=130,最优资源需求量上限Ei_opt2=230,最大资源需求量Ei_max=330,h=0.05,初始生长素含量Ci_0=1和Cj_0=1,概率p=0.5,概率p2=0.15,概率p3=0.75,斜率ε=0.01,M=3,生长素支付a=1,固定收益b=2,生长时间间隔Δt=1,生长素需求最大值Ci_max=9,根原基发育时间Tlim=3。 为了验证模型的有效性,以氮养分为例,设置了4种不同的根系生长环境:1)根系处于均匀低氮氮胁迫生长环境中(氮含量设置为90 μmol/L),记为符号LN。2)根系处于均匀高氮氮充足的生长环境中(氮含量设置为50 μmol/L),记为符号HN。3)首先根系生长处于均匀低氮氮胁迫生长环境中,经过一段时间后,部分根系处于均匀高氮氮充足的生长环境中(在仿真周期前15天,根原基分布于氮含量设置为50 μmol/L环境中;在仿真周期后5天,第10到第20个根原基分布于氮含量设置为90 μmol/L环境中),记为符号TLHN。4)根系处于异质的低氮氮胁迫,高氮氮充足和低氮氮胁迫的生长环境中(序号1~10个根原基分布于氮含量设置为50 μmol/L环境中,序号10~20个根原基分布于氮含量设置为90 μmol/L环境中,剩余根原基分布于氮含量设置为50 μmol/L环境中),记为符号LHLN。 图2为在进行10 000次仿真后,群体Parrondo博弈下环境环境影响的根分枝预测图示。在HN条件下比在LN条件下,根原基发展为根分枝的概率有明显的提升,该仿真结果与Mounier等[16]实验结果一致。在TLHN条件下,可以看出序号为10~20之间的根原基发展为根分枝的概率有明显的提高。该仿真结果与Zhang等[17]观察到的实验结果一致。在LHLN条件下,可以看出在氮含量丰富的区域,根原基发展为根分枝的概率更高,意味着该区域会有较多的分枝。该仿真结果与Giehl等[18]的实验结果一致。通过仿真实验结果表明,本文方法得出的根分枝预测能够实现对根原基转化为根分枝过程的建模。 为了便于对比分析本文方法与RootMap等方法在根分枝建模上差异,假设在国外主流的RootMap、RootTyp、SimRoot等方法中分枝间隔大小等于根原基发展窗口dw。图3给出了按照根分枝是向顶序列的思想在RootMap等方法中产生根分枝的示意图。可以看出RootMap等方法在建模根分枝时没有考虑环境资源分布不均以及环境资源分布随时间变化对根分枝的影响,仅仅按照分枝间隔等参数,以概率1产生分枝。在该过程中资源分布对根分枝的影响,是通过资源分布影响根伸长,从而影响根分枝数目。但本文方法资源分布不仅仅通过影响根伸长,影响根分枝数目,还通过影响根原基发育为根分枝的过程,实现对根分枝的建模。 图2 根分枝预测图示Fig. 2 Root branching prediction diagram 图3 RootMap等方法实现根分枝示意图Fig. 3 Root branching by RootMap etc 通过对基于群体Parrondo博弈的根分枝模型的分析,发现Parrondo博弈的结果对根原基群体的交互结果有着重要的影响。因此Parrondo博弈中A博弈选择概率p,B博弈中当生长素含量能够被M整除时博弈概率p2以及当生长素含量不能够被M整除时博弈的概率p3对根分枝有重要影响的参数(p2,p3的选择要满足负博弈的条件[19])。在LH条件下,通过设置不同的p、p2和p3值,分析参数调整对根分枝的影响(见图4)。从图4(a)可以看出,p值的选择对根原基发展为根分枝过程有重要的影响。当p值较大时(p=0.55),说明A博弈被选择概率较高。因此根原基间竞争加剧,从而造成根原基发展为分枝的概率有激烈的差异;当p值较小时(p=0.4),说明A博弈被选择概率较低,从而造成根原基间竞争强度降低,合作意愿加强,根原基更倾向于从外部环境中获取生长素,从而造成根原基发展为分枝的概率的差异相对较小。 在B博弈中,概率p2、p3的选择对于根原基发展为根分枝的过程也有重要的影响(图4(b)、(c))。直观上来看p2、p3增加,表示根原基从外部获取的生长素概率随之增大,因此根原基发展成为根分枝的概率也会增加。从图4(b)、(c)中可以看出,当p2=0.2或者p3=0.8时,根原基的分枝概率有很大的提高。当p2=0.1或者p3=0.7时,根原基的分枝概率相对较低。但p2表示B博弈中当生长素含量能够被M整除时博弈概率,因此p2对少部分根原基发展为根分枝的过程影响剧烈。从图4(b)可以看出根原基发展为根分枝的概率差异较大。概率p3表示B博弈中当生长素含量不能够被M整除时博弈概率,因此p3对大部分根原基发展为根分枝的过程会有影响。从图4(c)可以看出,当p3值增大后,大部分根原基发展为根分枝的概率会提高。 图4 在LN条件下不同 p、 p2、 p3值对根分枝的影响Fig. 4 Effect on root branching by p, p2, p3 under LN condition 根系结构的适应性变化对植物的生存具有重要的要义。根分枝是复杂根系结构形成的重要过程。但根原基发展为根分枝的过程展示适应环境变化的可塑特性,并不是一个序列过程。但现有根系生长模型中,通常把根分枝的产生视为一个向顶的序列。本文基于根原基受控顺序产生的特性,进一步把根原基视为智能个体,通过根原基个体对环境的感知以及根原基群间的竞争或者合作,通过根原基间的群体Parrondo博弈实现根原基的群体决策,从而实现根分枝可调制的预测,避免了传统根系建模与仿真研究中根分枝产生方式的不足,从而能够为植物建模与仿真整体研究提供模型支撑和分析手段,能推动植物建模与仿真应用于精确农业。2 仿真分析
2.1 仿真参数设置
2.2 仿真实验设置
2.3 仿真结果分析
2.4 Parrondo博弈概率对根分枝影响的分析
3 结语
