基于Hilbert-R树分级索引的时空查询算法

侯海耀，钱育蓉，英昌甜,2，张 晗，卢学远，赵 燚

(1.新疆大学 软件学院，乌鲁木齐830008； 2.新疆大学 电气工程学科博士后流动站，乌鲁木齐 830046；3.新疆大学 信息科学与工程学院， 乌鲁木齐 830046)(*通信作者电子邮箱qyr@xju.edu.cn)

0 引言

矢量时空数据高效组织管理是空间数据应用的关键技术，空间索引是实现矢量时空数据高效检索的关键[1-3]。空间、时间、属性作为时空大数据的三个基本特征[4]，如何描述和表达空间实体及其相互关系的时空变化，成为亟待解决的热点问题。

近年来，树形空间索引技术结合聚类技术来探讨空间索引技术的研究成为热门，对空间数据集进行有效聚类，其结果对构造高效的空间索引具有很大帮助[5]，但从时空查询角度出发，同时考虑所查询数据的时间维特征及各空间要素合理组织的研究较少，还不能很好地满足时空应用中对时空高效查询的需求。文献[6-8]侧重从空间数据分布的特点出发，采用聚类算法与R树结合构建索引，提高了空间查找效率；文献[9]提出基于Redis的缓存敏感R+树(Cache Conscious R+Tree，CCR+)，其查询效率较Oracle 10g的管理系统有较大的提升，但这些研究均未考虑对时间维建立索引。

基于以上问题，本文利用Hilbert曲线较为稳定的离散度分布特点[10]，分割并编码空间要素；利用动态确定K值的聚类算法，将聚类结果参与到Hilbert-R树构建当中，对矢量时空数据采用Redis丰富的数据结构进行分层组织存储；结合时间和聚类结果分层结构建立分级索引机制。在此基础上，进行数据密集型测试、时空范围查询及目标矢量对象查询，在真实数据集上进行，结果表明，提出的时间结合聚类分层组织存储及分级索引机制在时空查询性能方面较CCR+树有显著提升。

1 基础建模

1.1 时空数据建模

时空数据是用来描述现实世界中空间实体及各实体间随时间发展变化的过程和规律，它是描述矢量数据组织和设计空间数据库的基础[11]。本文参照国际标准化组织(Open GIS Consortium，OGC)制定的简单要素规范对矢量时空数据进行组织。每个时空要素有以下重要特征：

1)空间特征。指实际地物的几何特征(如形状、大小和位置)，以及各地物间的位置关系，通常用坐标(x,y)表示经纬度。

2)时间特征。通常指时空数据的空间特征和属性特征随时间而变化，本文数据集中的时间指采集该时空要素的时刻。

3)属性特征。空间实体的类别和属性。

基于以上特征，对时空要素可表示为[x,y,t,attrs]，其中：x、y分别表示要素横、纵坐标，采用经、纬度值代替；t表示采集该要素的时间；attrs表示时空要素的属性。

1.2 时空数据编码

本文对时空数据编码采用Hilbert曲线，其分形技术将多维空间区域等分为众多网格，并映射为一维区间，作为Peano族空间填充曲线家族中的分支之一，相对于Z-Order填充曲线，具有较优的空间聚类效果[12]。Hilbert曲线对空间相邻近特征的区域能够较好地表达，即在空间联系密切且空间几何距离相近的位置上，其曲线之间的距离也会较短[13]。如图1显示1、2、3阶Hilbert曲线，本文选用3阶Hilbert曲线进行研究。

图1 Hilbert曲线Fig.1 Hilbert curves

结合矢量时空数据，对Hilbert曲线进行描述如下：

1)等分区域(cell)的大小取决于Hilbert曲线的阶数λ，网格数m=22λ。

2)encodeNode(x,y)，利用Hilbert编码规则将空间S内的坐标(x,y)转换为Hilbert值。

3)encodeSegment(x1,y1,x2,y2)，将空间区域内的坐标范围(x1,y1,x2,y2)转换为一系列Hilbert范围值，即一维区间。

1.3 空间聚类建模

针对时空数据空间部分采用树形空间索引易产生大量重叠和死空间，考虑将空间上相邻的数据存放于同一子树下，即与聚类技术结合的方式，在减少数据存储冗余及I/O寻道时间、提高检索效率等方面具有重大的研究意义。目前多数聚类算法的结果易受初始K值及离群空间数据的影响[14]，本文在对空间要素对象进行Hilbert曲线编码后，依据空间要素分布特点，定义距离函数和均方差准则函数。

定义1 距离函数。由r1、r2、…、rn组成的n个Rd空间要素集合，设oj为第j个类的聚类中心，则ri与oj的距离为：

(1)

定义2 均方差准则函数。为使聚类效果满足“类内紧凑， 类间分离”的原则，需要聚类测度函数进行衡量，均方差准则函数如下：

(2)

其中:k为聚类数；i为Sj中的数据；o为Sj的聚类中心。算法思想：将k=1作为初始聚类，再令k值递增，每次递增后，都将通过计算得到新的聚类中心，使所有类中数据与聚类中心的距离平方误差之和最小。递增k值后，比较函数值E，若该值收敛，则将k值作为聚类数；若不收敛，则继续递增k值。经分析，该算法的复杂度为O(nkt)，其中n指空间要素对象的个数，t指算法迭代次数。通常k≪n且t≪n，因此该算法时间复杂度接近线性，适合处理大规模的时空数据。

2 面向Redis的时空索引

2.1 构建基于动态定值聚类的 Hilbert-R树

目前，R树及其变体的构建以空间要素逐一插入的动态过程为多，而此处的Hilbert-R树是静态批次构建的过程，在对空间要素进行Hilbert编码之后，根据定义1的距离函数选取两两距离最大的空间要素作为初始聚类中心，以使类间相似度较低，而类内相似度较高。递增聚类数K值，遵循层次聚类中的分裂思想，找到距聚类中心最远的空间对象及距该空间对象最远的另一空间对象，将二者作为新的聚类中心，开始聚类；根据定义2的均方差准则函数，计算并比较K值变化(即每次聚类)后的函数值，若该值收敛，可将当前状态视为聚类结果；否则，继续递增K值。对Hilbert-R树的构建步骤阐述如下：

1)以某个时刻T(t0≤T≤tn)的空间数据集为研究对象，计算该数据集下所有空间要素的最小包围矩形(Minimum Bounding Rectangle，MBR)及其中心。

2)调用聚类算法，产生以空间点要素及空间要素MBR为对象的K个聚类。

3)计算所得各聚类内包含空间要素对应的Hilbert值，并对该值进行升序排序。

4)依据节点最大容量M(Msize≤32 MB)，对排列好的空间要素构建叶节点。若聚类内空间要素数小于等于M，则该聚类内的所有空间要素构成一个叶节点；反之，则生成多个含有M个空间要素的分组，并按生成顺序构建叶节点。

5)依据生成顺序自底向上地构建各层中间节点和根节点，进而生成基于聚类的Hilbert-R树。叶节点存放聚类所包含空间要素MBR对应的Hilbert值，各层中间节点则存放其子节点的Hilbert最大值。

基于动态定值聚类的Hilbert-R树构建算法如下：

输入tList=(t0,tn)。

输出Hilbert-R树。

Begin

foreachelementintList

element.MBR=cal()

endfor

myKNN_List=myKNN(tList)

my_HilbertValue=statistic(myKNN_List)

my_SortValue=sort(my_HilbertValue)

ifvalue<=Mthen

Hilbert-R=Create_tree(value,my_SortValue)

elseif

myGroup=Group(value,my_SortValue)

Hilbert-R=Create_tree(value,myGroup)

endif

returnHilbert-R

end

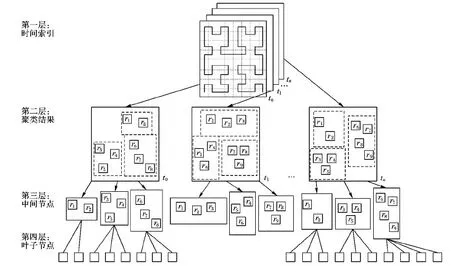
图2 分级索引结构Fig.2 Hierarchical index structure

2.2 建立分级索引结构

经上文Hilbert-R树的构建可知，Hilbert-R树具有中间节点和叶节点两种节点结构，依据Redis数据库Key-Value方式对时空数据进行存储。

选择Redis作为时空数据存储数据库的原因如下：Redis是分布式非关系型数据库之一，是一种具有高性能键值对的内存数据库。其中，键值(key)是Redis存储数据的重要依据，具有唯一性，同时也作为对数据检索、定位、修改和删除的根本因素[15]。Redis中的键值对类似于关系数据库中的行和列，不同的是value这一列可以存储多个条目，而不是只能存储一个值[18]。Redis支持丰富的数据结构，用于满足不同的矢量时空数据存储要求，包括：string、list、set、zset(sorted set)、hash等多种键值数据类型。这些数据类型都支持取集合的交、并、差等多样操作，还支持不同方式的排序，并且这些操作都是原子性的。此外，Redis为用户提供了可靠的持久化方案和主从复制功能，以确保数据的安全性。基于以上特性，Redis可以保证对矢量时空数据的存储和管理。

本文提出一种分级索引机制，将该时空数据库结构划分为已聚类的空间部分和时间部分。整个时空数据集被周期化的时间值(以小时为单位)所划分，即每个空间数据集对应不同的时间值，因此将时间部分的索引建立于第一层索引结构中；对某一时刻T的聚类结果(即Hilbert-R树中具有相同时间值的中间节点)进行索引信息的存储构建；而对空间要素的索引建立在Hilbert-R树的中间节点之上，即图2第三层，中间节点存放其子节点的最大Hilbert值。基于以上分层分级的索引结构，查询某个时空数据可以先通过时间索引，确定该时刻的空间聚类信息，再利用高效的Hilbert-R树定位于目标对象。具体分层分级索引结构及其在Redis数据库中的存储方式如图2所示。

第一层 时间索引信息存储，采用Redis数据库中的有序集sorted set数据结构对时空数据集元数据信息中唯一对应的时间值进行组织，可以通过key=Index:T的格式访问对应的数据集，将时间值[n,n-1)作为sorted set使用的排序码，如表1所示。

表1 时间索引信息存储结构Tab.1 Information storage structure of rime index

第二层 调用聚类函数，将某一时刻[n,n-1)下的空间要素(r1,r2,…,rn)进行聚类操作，得到K个聚类结果。统计类中要素的Hilbert值，并升序排列。

第三层 中间节点索引信息存储，针对同一时间下不同聚类结果的索引采用Redis的sets数据结构进行组织，通过key=Index：T：Index_I可以访问具体的聚类索引项，即Hilbert-R树的中间节点，它们都具有相同的时间属性，具体结构如表2所示，In数为Tn时刻的聚类个数。

表2 分级索引信息存储结构Tab.2 Information storage structure of hierarchical index

第四层 Hilbert-R树的叶子节点，即各聚类内所包含的空间要素(r1,r2,…,rn)。

最后将Hilbert-R树的中间节点元数据信息利用Redis数据库中的sets数据结构进行组织，用于存放叶子节点的最大Hilbert值。如表3所示，其中(rh1,rh2,…,rhn)表示各叶子节点所对应的Hilbert值。

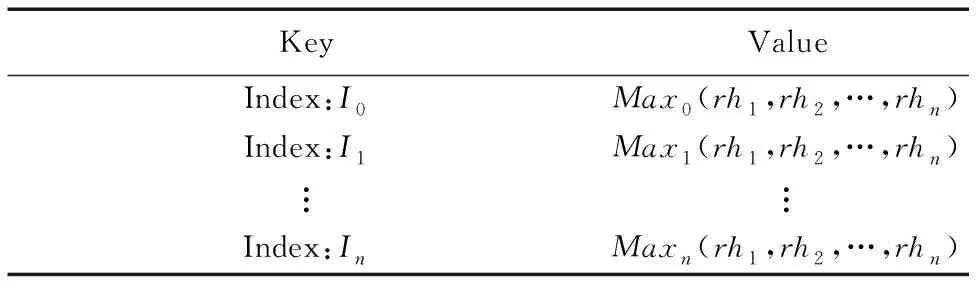
表3 中间节点信息存储结构Tab.3 Information storage structure of intermediate node

2.3 基于Hilbert-R树的时空查询流程

时空范围查询的基本思想：根据查询空间范围(x,y)或(x1,y1,x2,y2)调用函数encodeNode(x,y)或encodeSegment(x1,y1,x2,y2)并转换为对应Hilbert值或Hilbert范围值；同时结合所查询时间值调用第一级时间索引，确定查询目标所对应的Hilbert-R树中，递归调用Hilbert-R树索引结构，对树中空间要素与查询对象进行精准相交检测，直到输出查询结果。图3是时空查询算法流程。

3 实验分析

实验采用Redis 2.6标准版，操作系统为CentOS release 6.5 64 bit，硬件环境配置为：Intel Core i7-4790 CPU @3.60 GHz，8 GB内存，500 GB硬盘。实验数据集采用ShapeFile格式的乌鲁木齐市道路交通数据，选取了2011—2014年的数据。考虑时空范围和空间分布两个因素，分别进行了数据密集型测试及目标矢量对象测试，最后进行时空范围查询综合测试，实验对比文献[9]中的CCR+树，并对本文方案技术特点进行验证如下。

3.1 数据密集型测试

本实验选取相同时空范围内不同空间分布状况的数据集对Hilbert-R树及CCR+树[9]对空间索引性能的测试。

在定义1的基础上，定义P为平均分布状态[6]:

(3)

其中：li(i=1,2,…,n)表示空间数据的邻近对象个数；P值的大小反映了空间分布的密集状态。如表4所示数据集T1、T2的P值较大，则说明空间分布状态较密集；而数据集T3、T4的P值接近1，表示二者空间分布较均匀。

表4 空间数据分布状态Tab.4 Distribution of spatial data

不同空间分布下，Hilbert-R树与CCR+树的查询耗时结果如图4所示。在不同密集程度下，经聚类后的Hilbert-R树的查询耗时约为CCR+树的一半，说明前者查询耗时较短，进一步验证了数据是否平均分布对本文算法的查询效率影响不大。这是因为本文算法充分考虑了空间要素的分布特点，动态确定K值的聚类算法尽可能地将空间分布相近的要素聚为一类，经有效聚类后构建Hilbert-R树，提出分层分级的索引结构，将聚类结果在同一子空间的要素组织在同一子树下，较大程度上降低中间节点间的重叠，对分布不均匀的空间要素得以正确处理，从而提高索引操作的性能。

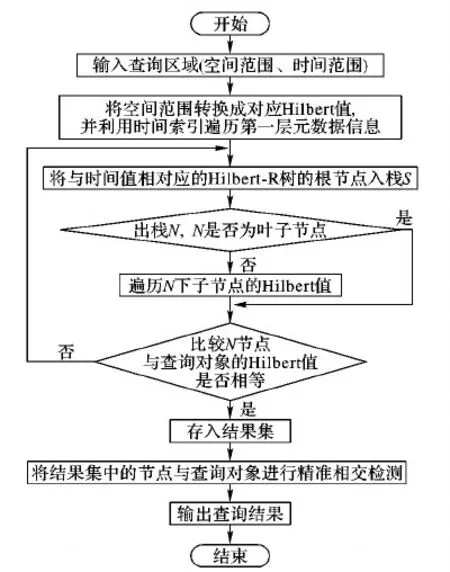
图3 时空查询算法流程Fig.3 Flow chart of spatial-temporal query

图4 不同分布状态下CCR+和Hilbert-R的查询对比Fig.4 Contrast of CCR+ and Hilbert-R in different distribution states

3.2 目标矢量对象查询

为进一步分析空间分布相同(分别选取分布密集和均匀的情况下)不同时空范围下针对目标矢量对象的查询，本实验数据采用时空数据生成器(Generator of Spatio Temporal Data， GSTD)生成不同的时空范围模拟数据集，其中:D1～D5的P值都等于3.44，D6～D10的P值都等于1.05，分别选取不同时空范围的区域进行研究，对应矢量对象数目也不尽相同(如表5所示)。GSTD是一个被广泛认同的目标对象数据集生成器。利用所生成的诸模拟数据集分别查询目标矢量对象，计算各自访问节点数目的平均值，以此反映Hilbert-R树与CCR+树的查询效率。

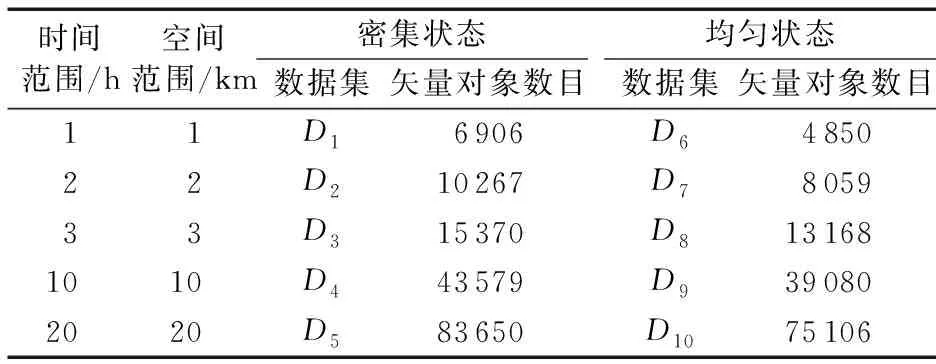
表5 样本数据集描述Tab.5 Sample data set description

图5和图6分别展示了密集分布和均匀分布下，Hilbert-R树与CCR+树对目标矢量对象查询时，二者平均访问节点数目的情况：

1)CCR+树访问节点数与数据集的数量呈正比例增长的趋势；而Hilbert-R树无论在分布密集还是均匀的情况下，对节点访问数的增幅都不明显。

2)随数据集的增大，Hilbert-R树对节点访问的变化率较CCR+树稳定，从而验证了本文算法查询效率对数据量的变化不敏感，受数据分布状态的影响不大。

这是因为CCR+树进行查询时从索引树的根节点开始，依次遍历存储于其中的空间要素，节点间被动搜索满足条件的叶节点，有可能会遍历整棵树。

图5 密集分布下的访问节点数对比Fig.5 Comparison of access nodes under dense distribution

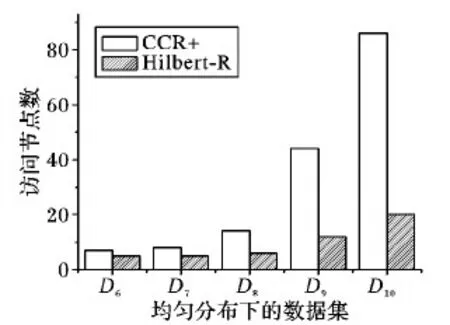
图6 均匀分布下的访问节点数对比Fig.6 Comparison of access nodes under uniform distribution

本文在构建Hilbert-R树的过程中充分考虑了实际时空数据的分布特点，利用聚类方法使得Hilbert-R树结构更加紧凑。算法动态寻找最优K值将数据对象划分为多个类，自底向上逐层构建树结构，确保数据精准划分，迭代重定位使划分逐步改进，同时分层分级索引结构的提出对时间维的查询更加便捷，避免访问多余节点，有利于需要同时考虑空间和时间的目标矢量对象的查询。

3.3 时空范围查询

本实验选取了2013年2月1日—2日的车辆轨迹数据(共包含30 177条记录数)作为实验数据对聚类的Hilbert-R树及CCR+树进行时空范围查询的综合测试，选中从第5084条记录数开始，以平均间隔约5 000条递增的数据量(包括第5084、第10850、第15065、第20037、第25085、第30177条记录数)分别进行10次测试后，取查询耗时的平均值。

图7对比了聚类的Hilbert-R树与CCR+树在不同数据量下的时空范围查询效率，可分析得到：

1)Hilbert-R树的查询耗时与数据记录数量的关系呈线性正相关；

2)Hilbert-R树相比CCR+树的查询耗时平均缩短了约25%；

3)随着数据量的增大，Hilbert-R树的查询响应时间优势较CCR+树更趋明显。

经分析发现，在对时间范围方面的查询时，由于CCR+树并未考虑时空数据的时间属性，将其归入空间属性的另一维，致使整个多维空间数据不能协调分布，节点间频繁访问，徒增查询开销。

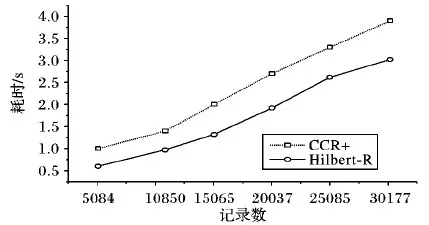
图7 时空范围查询结果Fig.7 Results of spatio-temporal range queries

然而Hilbert曲线本身具有良好的数据聚集特性，聚类后的Hilbert-R树的构建对不同分布的空间要素进行处理，使相邻空间要素聚集于相邻中间节点之上，减少了R树节点间的重叠，使得查询所需访问的节点数更少，提高了查询效率；同时本文提出的分层分级索引结构充分考虑了时间属性，时空数据依时间—空间合理组织，对于查询性能的提升也起到了重要作用。

3.4 结果分析

为了探索在不同空间分布及时空范围下，Hilbert-R树及CCR+树对矢量时空数据的查询情况，本节采用ShapeFile格式的乌鲁木齐市道路交通数据展开实验，分别对Hilbert-R树及CCR+树的数据密集型、时空查询效率和目标矢量对象查询进行了测试。分析以上实验结果可得出结论如下：

1)聚类后的Hilbert-R树分层分级索引结构受数据分布状况的影响不大，因此适用于对空间分布不均且局部密度较大的时空数据查询；

2)随数据量的增加，Hilbert-R树相对于CCR+树的时空查询效率更高，其访问节点数更少，因此适用于时空范围较大的矢量数据。

综上，采用聚类的Hilbert-R树分层分级索引结构可开展时空大数据存储及查询算法的应用，在内存数据库支持下进行多尺度、多类型的时空数据查询，为时空地理信息系统(Geographic Information System, GIS)的发展奠定理论基础及方法借鉴。

4 结语

鉴于时空数据的矢量查询应用中缺乏对时间维和空间要素合理组织的考虑，本文从时空数据的空间分布出发，提出基于Hilbert-R树分级索引的时空查询算法。该算法利用Redis丰富的数据结构对周期化的数据集建立时间索引，经Hilbert曲线划分并编码空间部分，在此基础上进行聚类处理；将空间聚类结果与时空数据的时间属性结合，建立Hilbert-R树的分层分级索引结构。经实验验证，所提算法有效降低了时空查询的时间开销，且对树节点的访问量不大，查询耗时受不同数据分布密度的影响较小，更适合Redis对海量时空数据高效查询处理的需求。

下一步研究工作将优化Hilbert-R树索引构建，引入机器学习算法对时空轨迹模式挖掘进行研究，使时空查询效率更高。