Q3黄土的一维扰动演化规律试验研究

徐亚利

(合肥学院 建筑工程系，安徽 合肥 230601)

岩土材料是大自然孕育的一种天然建筑材料，而它与其他材料根本不同之处正是这种天然赋予它的随机性，这种随机性让土体具有大小不一的不均匀性和与生俱来的结构性，所以天然土绝大多数都具有一定的结构性。土体的本构关系一直岩土界研究的古老而又崭新的课题，因此，近些年来考虑土体结构性的研究已经成为本构问题的研究重点和热点。而黄土既是一种典型的特殊土也是结构性较强的一种土体，其特殊的地质条件和自然环境下形成的微结构造就其力学性质的复杂性，使其常表现出欠压密性、结构性、水敏性以及由此表现出的各向异性等，对于黄土结构性及其本构模型的研究方面很多学者利用各种手段及相关理论也都做了大量工作，取得了丰硕的研究成果。如高国瑞利用微观测试手段在其微细观研究上做出了很多研究，给出了在微观上度量其结构性变化的本构关系[1-2]。沈珠江在损伤力学基础上考虑其结构性的损伤变化发展了一系列的本构模型[3-4]。谢定义及其弟子在土力学理论基础上提出了综合结构势的概念及其相应的本构模型[5-7]。也有学者采用扰动状态概念开展了结构性土的本构关系研究，然而以此理论开展黄土本构关系的研究却鲜有报道。扰动状态理论(Disturbed State Concept, DSC)因其基于了平均化的思想，不仅吸收了诸多理论的优点[8-9]，如损伤力学、临界状态和连续介质等理论，而且将扰动函数作为联系宏观和细观的桥梁，通过扰动函数能有效地反映细观变化和宏观力学响应的演化过程[10-14]。

为此，本文基于扰动状态理论的思想，考虑黄土的结构性对黄土压缩特性的影响，首先以孔隙比为参变量定义了一维压缩下的扰动函数，并对扰动函数的演化规律进行研究，拟合得到黄土的扰动演化规律方程。其次，考虑含水量其对结构性的影响，通过不同含水量的变化，研究反映结构性的扰动函数的变化规律，从而为黄土结构性研究、路基的固结和沉降提供理论指导和参考价值。

1 扰动状态理论

扰动状态概念(Disturbed State Concept缩写为DSC)的思想，是研究材料本构关系中考虑材料受到外界扰动后材料微结构发生变化，即考虑度量这种扰动后变化的一种本构关系模拟方法[9]。然而该理论不仅不需要在微观上定义本构，更巧妙地回避了微裂纹相互作用中的种种难题。扰动状态理论认为：从微观方面来说，各种因素的外界作用力，一旦发生作用就会对材料微结构产生一定程度的扰动，其内部微结构就会产生相应的变化，这种微观的变化必然是由一种被扰动的不稳定状态逐渐向另一种趋于稳定状态的过渡，最终使得其微结构能在该扰动状态下稳定下来足以承受外部荷载的作用。同时，在宏观方面来看，微观结构的变化必然会在其宏观力学性质上发生相应的变化，这种力学性能的变化也恰恰印证了其微观结构上做出的调整。因此，扰动状态理论不仅能够回避直接对微结构变化的定量度量问题，还可以通过因扰动在微观结构的变化去解释其在宏观力学上表现出来的力学性质的响应。因此，需要借助一个函数去描述或表达反映这种扰动过程，即扰动函数D(扰动因子)。与此同时，通过相应的宏观试验去测得该微观结构的变化，并定义恰当的扰动因子来表达或描述其结构上的变化，从而达到了模拟材料的本构关系。如图1所示。

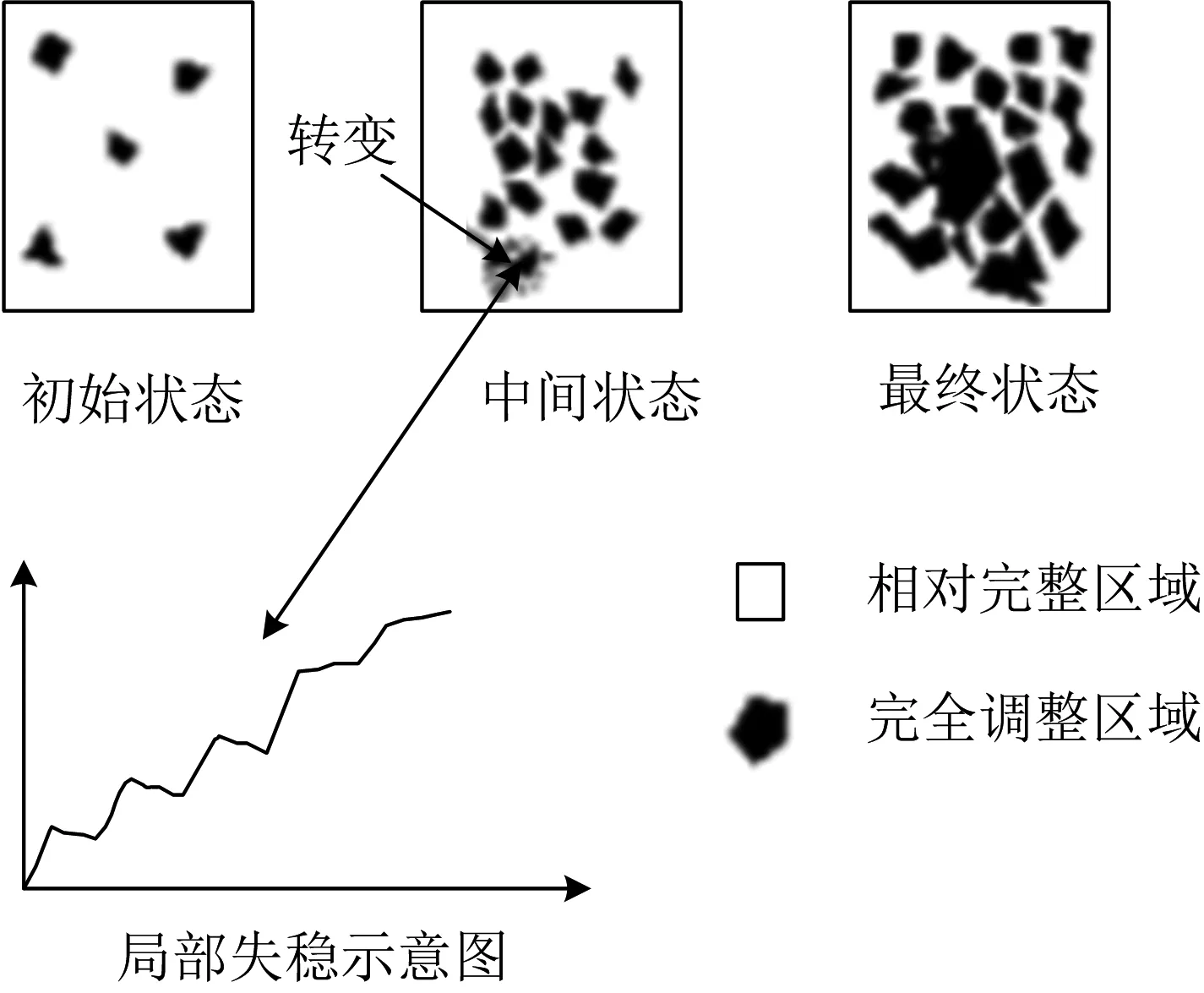
图1 扰动状态的基本原理示意图

假定材料单元中由两种状态随机构成的混合物，即相对完整状态(RI)和完全调整状态(FA)，针对这两种状态的特性，可以分别考虑用不同理论和模型去模拟，然后通过定义恰当的扰动函数来实现对实际材料的这两种状态之间的变化关系，研究其材料受到扰动后的演化规律，从而进一步构建本构关系。如图2所示。

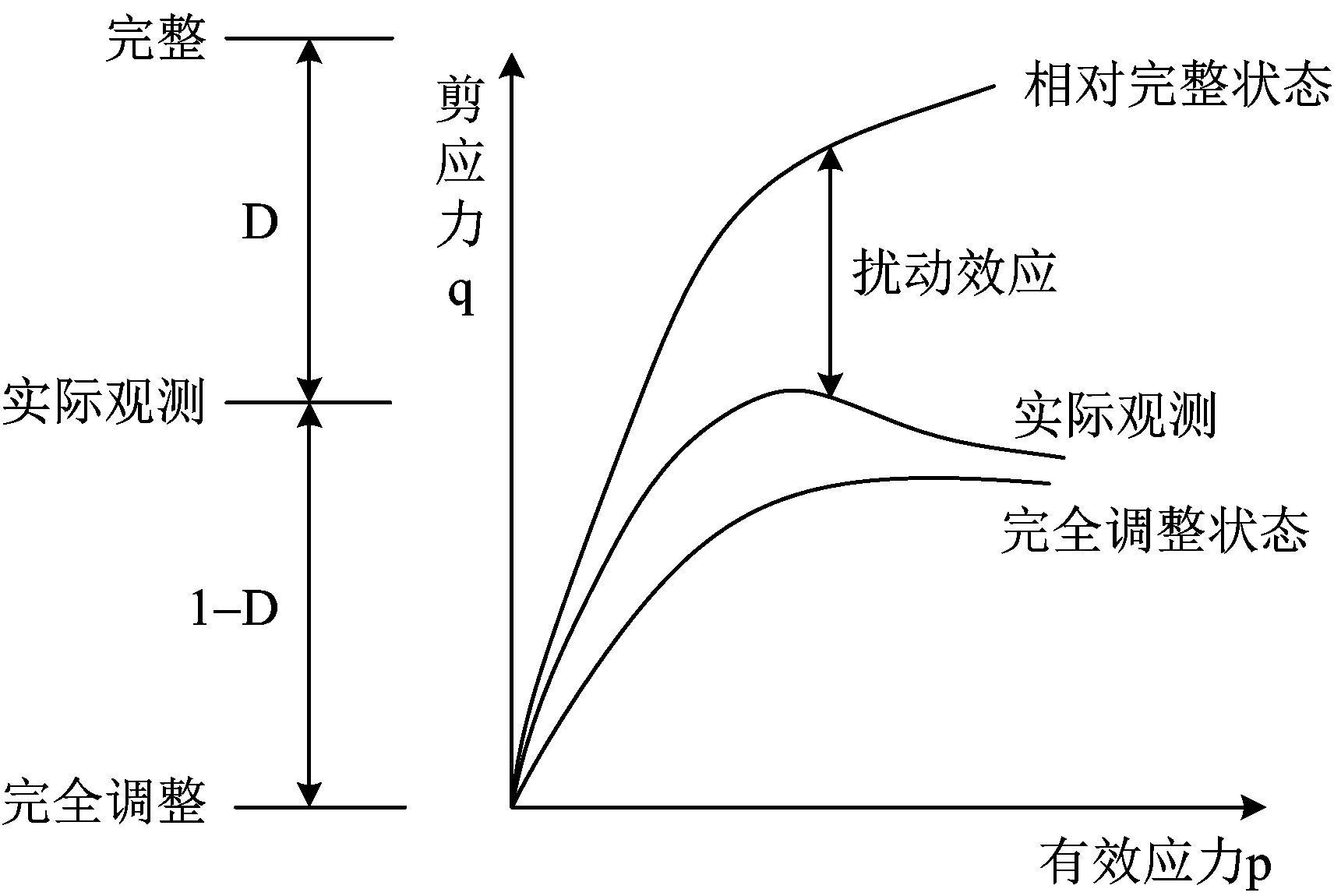
图2 扰动状态概念描述材料力学响应的示意图

2 黄土的物理力学性质与试验结果

2.1 黄土的物理力学性质

为了揭示黄土结构性，更好地说明其微观结构性与宏观扰动函数演化规律的内在机理，针对黄土的欠压密、高强度和水敏性及的特点，分别设计了原状Q3黄土和重塑Q3黄土在不同含水量下的侧限压缩试验。

试验土样取自西安市北郊的某工地，取土深度为5.0 m左右。所取土样属典型的Q3黄土，其物理力学性质指标如表1所示。

表1 原状黄土的物理与力学性质指标

2.2 试验结果

2.2.1 不同含水量下原状土样的压缩曲线及分析

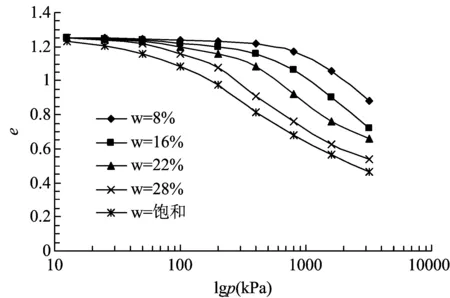
图3 不同含水量的原状土压缩曲线

由图3可见，含水量的变化对原状Q3黄土压缩性影响相当显著，尤其在初始结构破坏前后，其曲线表现出的有无拐点的特征尤为明显。

2.2.2 不同含水量下重塑土样的压缩曲线及分析

由图4可见，重塑土在不同含水量下其曲线变化不大，除了低含水量时表现出微弱的次生结构外使得曲线有拐点外，其他情况下的曲线相对呈线性而无拐点，这也恰恰说明重塑土因制样原因已经丧失了原有的结构性。

3 扰动函数及演化规律

3.1 扰动函数的提出及演化规律研究

试验已经证明：具有结构性的原状黄土，其压缩性在屈服前后是有明显的变化的，而且这种变化恰恰就是黄土的结构性被打破前后的反映，所以与土的结构性有着直接的关系。也正因为土结构性的存在，才导致原状土与重塑土在受到相同荷载作用下有着不同的力学表现。由于随着荷载的增大，土体的结构性逐渐被破坏，因此恰当的扰动函数应该是不仅能度量土的结构性影响大小而且又能反映加载应力的函数。对于黄土而言，其显著的水敏性，正是使得其天然含水量的不同，其浸湿以后的结构性的变化和湿陷变化量不同，故扰动函数应该能反映含水量对其结构性的影响。因此，在侧限压缩试验中，压缩变形的发展是以体积的变化为反映，其实质则是以孔隙比作为其具体的体现，其孔隙比的变化也正是其结构性损伤的一个表征，因此，本文以孔隙比作为参变量来定义扰动函数，即：

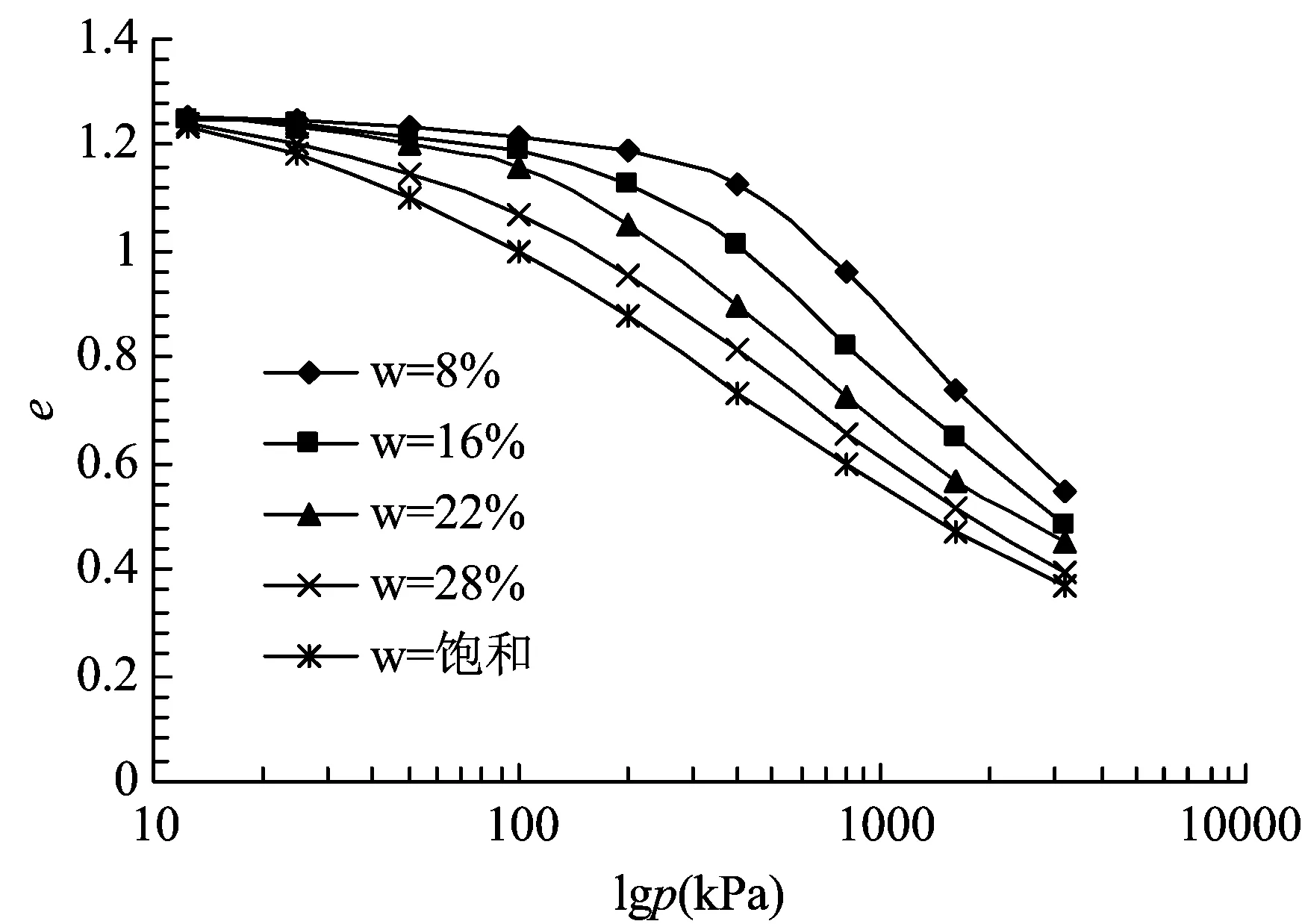
图4 不同含水量的重塑土压缩曲线

(1)

其中，e0为初始孔隙比，e为某级荷载下原状土样对应的孔隙比，ec为最后一级荷载作用下对应的孔隙比。

由式(1)可以得到原状土和重塑土的单参数扰动函数的演化规律分别如图5和图6所示。

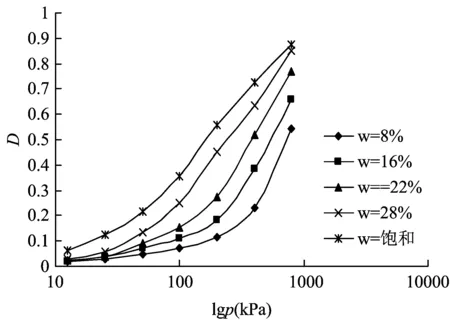
图5 原状土的扰动函数演化规律曲线

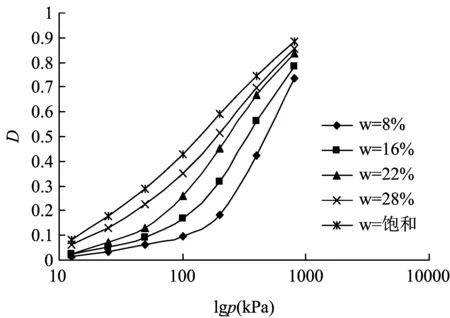
图6 重塑土的扰动函数演化规律曲线

由图5和图6可见，原状土和重塑土的以孔隙比为参变量的扰动函数的演化规律可以拟合为：

D=1-Aexp(-Blgp)

(2)

其中，A、B为其扰动函数的参数。

3.2 含水量对扰动函数参数的影响

通过最小二乘法分别拟合得到原状土和重塑土的扰动函数中参数A和B的值，具体可见表2所示。

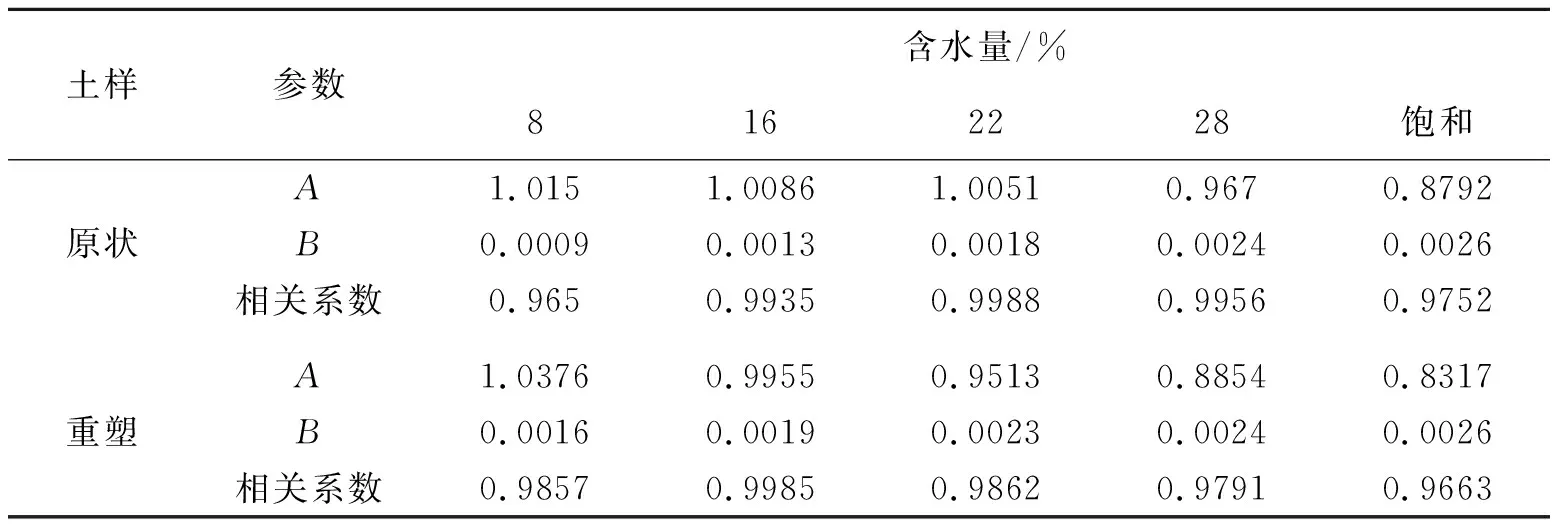
表2 原状土和重塑土不同含水量的扰动函数参数A和B的值

通过上述分析以及拟合的结果可见，扰动函数D随着含水量的变化而变化，且呈较好的规律性，含水量对其参数A和B也有较好的规律性，其影响规律、拟合参数及相关系数如图7和图8所示。

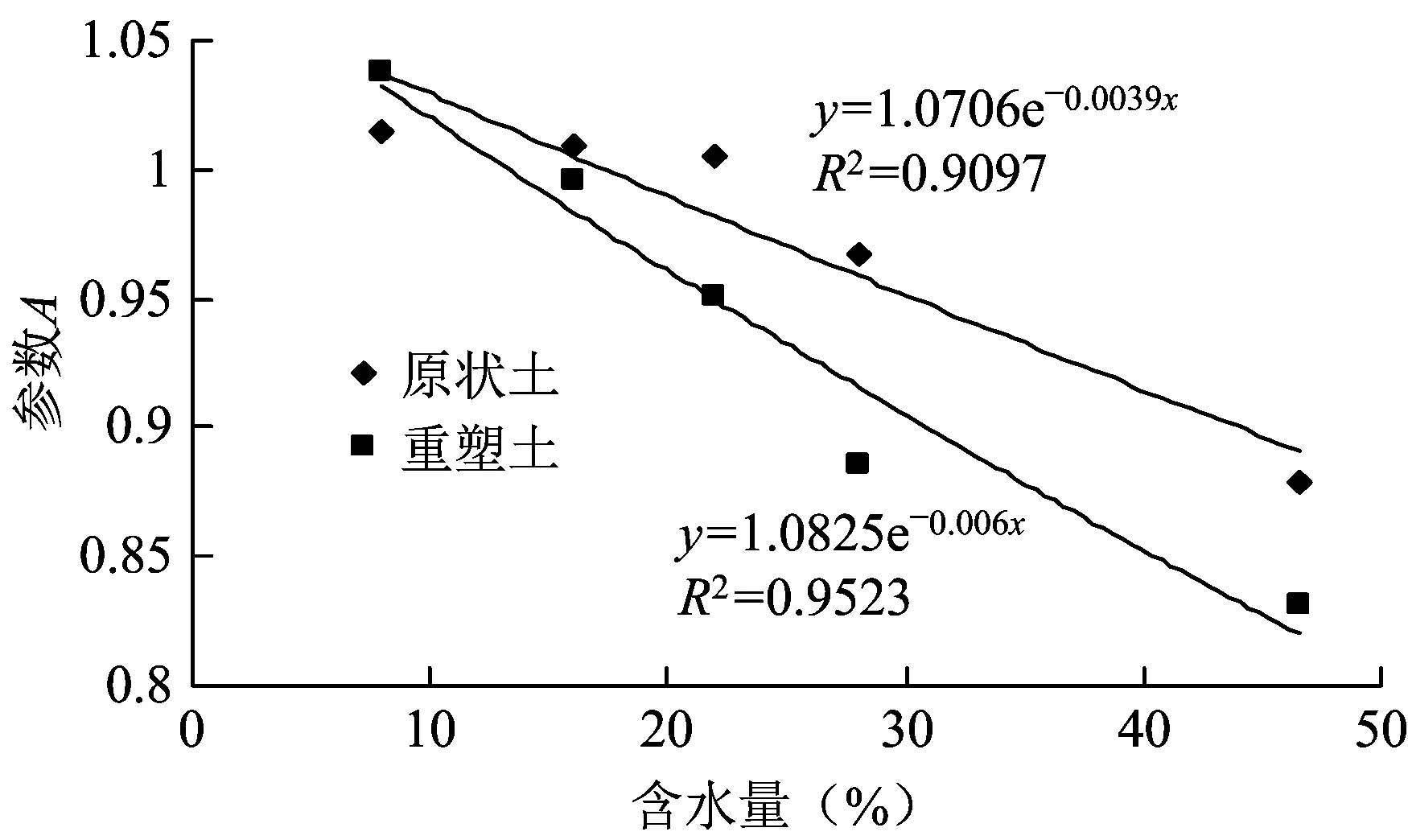
图7 含水量对扰动函数中参数A的影响规律

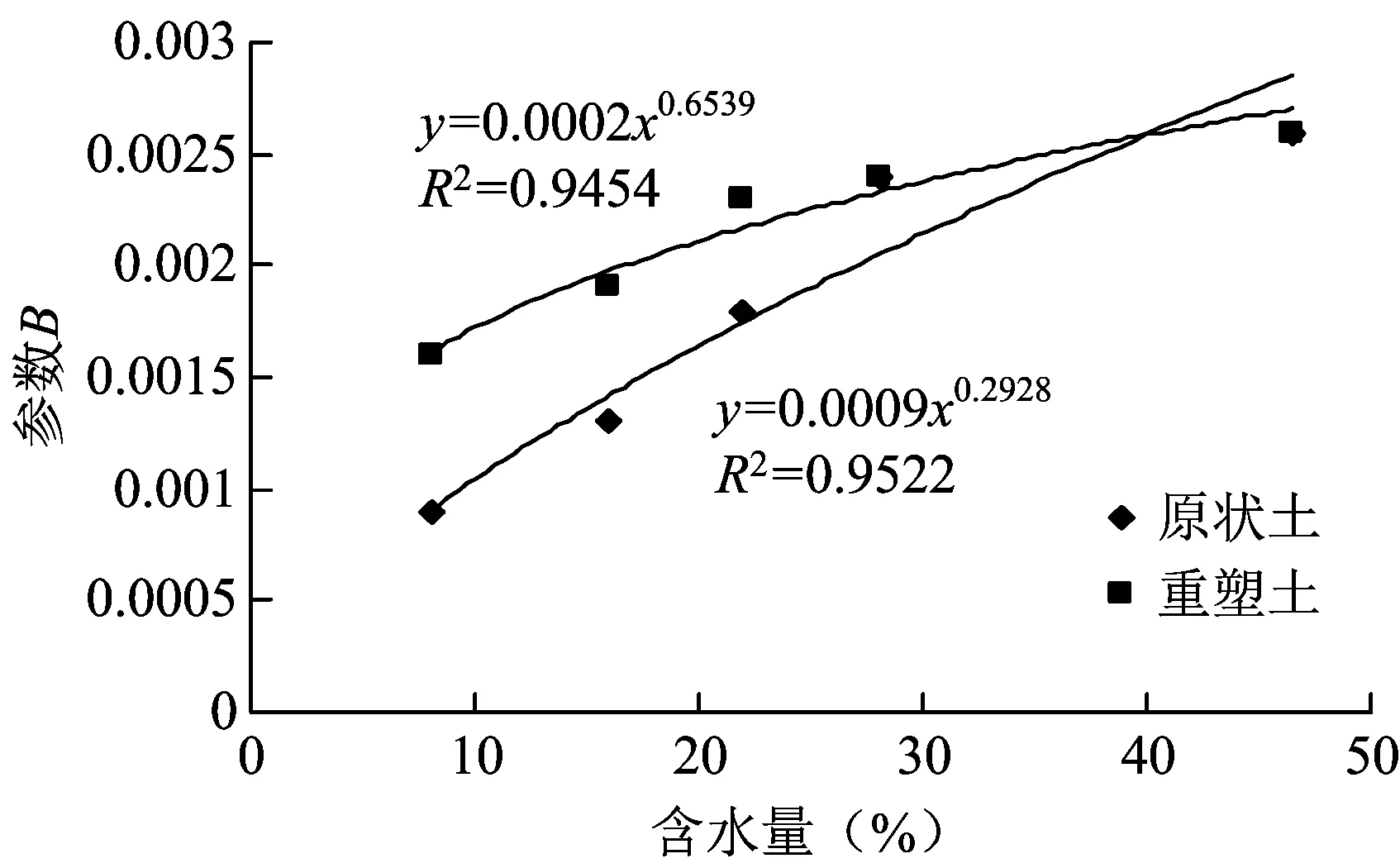
图8 含水量对扰动函数中参数B的影响规律

由图7可见，可用指数函数拟合含水量对原状黄土和重塑黄土的扰动函数中参数A的影响规律，即：

A=a1eb1w

(3)

由图8可见，可用幂函数拟合含水量对原状黄土和重塑黄土的扰动函数中参数B的影响规律，即：

B=a2wb2

(4)

4 结论

本文基于扰动状态概念的思想，结合结构性对黄土压缩特性的影响规律，定义了以孔隙比为参变量的扰动函数，研究了扰动函数的演化规律，进一步分析了含水量对扰动函数参数值的影响。主要得到以下结论：

1)基于扰动状态概念的思想，结合结构性对黄土压缩特性的影响分析，定义了以孔隙比为参变量的扰动函数，研究了扰动函数的演化规律，得了扰动函数的演化规律方程。

2)分析了含水量对扰动函数的演化规律方程中参数的影响，研究表明：含水量对扰动函数的演化规律方程中参数A的影响规律符合指数函数，对扰动函数的演化规律方程中参数B的影响规律符合幂函数。

3)黄土的扰动演化规律为黄土路基的固结和沉降提供参考价值和理论基础。