一道高考题的改编题之初中解法

☉江苏省南京金陵中学河西分校 李玉荣

这是2008年江苏省高考数学试卷第13题，时下最值问题是中考的热门题型，于是有热心的网友在某初中数学教师教研群里晒出了由它简单改变的一道题：

题2：△ABC中，AB=4，AC=2BC，求△ABC的面积的最大值.

作为一名初中数学教师，笔者看到了一些高中解法，总觉得不够简洁，此题能用初中知识求解吗？笔者饶有兴趣地作了研究，竟有一些意外收获，撰写此文与大家分享.

解法1：如图1，设BC=x，AC=2x.

评注：此解法依据海伦公式，直接利用配方法求解，方法自然.

解法2：如图2，作CD⊥AB，垂足为D.

设AD=x，BD=|x-4|，CD=y.

根据勾股定理，得AC2=x2+y2，BC2=（4-x）2+y2.

因为AC=2BC，所以x2+y2=4［（4-x）2+y2］，解得y2=-x2+

评注：△ABC中，AB为定值，故只需求AB边上的高的最大值即可，此解法利用勾股定理建立关系，借助配方法确定y的最大值解决问题.

解法3：如图3，作CD⊥AB，垂足为D.

评注：此解法与解法2类似，不同点在于利用勾股定理得到面积与x的关系，再借助一元二次方程根的判别式直接求得最大值.

解法4：如图4，分别作∠ACB及其外角的角平分线，交AB及AB的延长线于点D、E，则∠DCE=90°，且=2.

因为∠DCE=90°，所以点C在以DE为直径的圆上.

评注：△ABC中，AB为定值，故只需求AB边上的高的最大值即可，此解法巧作两条角平分线，获知点C在一个定圆上，从而确定高的最大值，问题得解.

解法5：如图5，在AC上取点D，使得∠DBC=∠BAC.又因为∠BCD=∠ACB，所以△BCD △ACB.

由于AB=4，BD=2，所以当DB⊥AB时，△ABD的面积最大，最大值为

评注：此解法巧构相似三角形，转化为求△ABD的面积的最大值.而△ABD有两条边的大小确定，故当其夹角为直角时面积最大，问题轻松得解，令人拍案叫绝.

解法6：如图6，在AB的延长线上取点D，使得∠DCB=∠DAC.又因为∠BDC=∠CDA，所以△BDC△CDA.

设BD=x，则 CD=2x，AD=4+x.

可得（2x）2=x（x+4），解得，所以

评注：△ABC中，AB为定值，故只需求AB边上的高的最大值即可，此解法巧构相似三角形求出CD，进而解决问题，解法独具匠心.

学习在于思考，解题更要勤于思考、善于思考.尽管受初中数学知识的局限，能用来求解的高考题稀少，但如果题目仅仅涉及平面几何知识，大可让学生挑战自我，放手一试，一旦成功，必将增强他们解题的自信心，提升学习数学的兴趣，起到意想不到的教学效果.令人欣慰的是，笔者从2018年江苏省数学考高试卷又斩获一例：

题3：（2018年江苏省高考数学Ⅰ第13题）在△ABC中，内角A、B、C所对的边分别为a、b、c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为______.

解：如图6，作DE∥AB交BC于点E.

则∠EDB=∠ABD=∠EBD=60°.所以△BDE为等边三角形.

从而BE=DE=BD=1，CE=a-1（a＞1）.

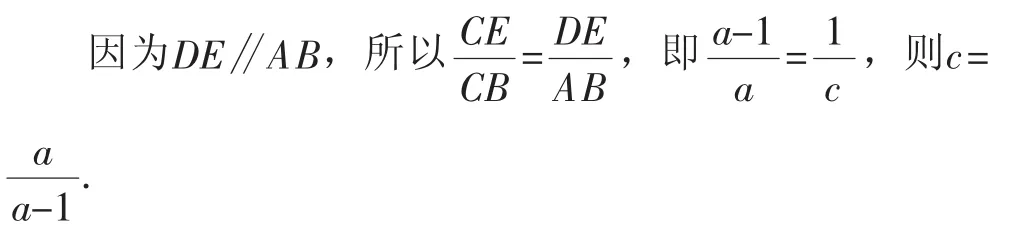
令y=4a+c.

由Δ=（y+3）2-16y≥0，解得y≥9，故4a+c的最小值为9.