一道国际几何竞赛试题的多种证明与教学启示

☉北京教育学院朝阳分院 白雪峰

第四届伊朗几何奥林匹克竞赛于2017年9月7日举行，有43个国家和地区参加了此届竞赛.我国派出了北京市、上海市、南京市、杭州市的20所学校参加了此次比赛.比赛分为三个组别：初级组（七、八年级），中级组（九、十年级），高级组（十一、十二年级）.［1］笔者基于对初级组第3题的探究，在给出多种证明方法的同时，阐述了对初中平面几何教学的思考与启示.

一、问题及其分析

问题：如图1，在正五边形ABCDE中，过点C作CD的垂线，与边AB交于点F.求证：AE+AF=BE.

分析：证明的结果是两条线段AE、AF的长度之和等于第三条线段BE的长度，而证明此类问题的通性、通法是“截长补短法”.下面，笔者就利用这一方法证明本题.

为使多种证法简洁、流畅，突出对问题本质的透视，笔者首先把在多种证明方法中反复应用的条件一一给出证明，以便在后续证明中能够直接应用这些结论.

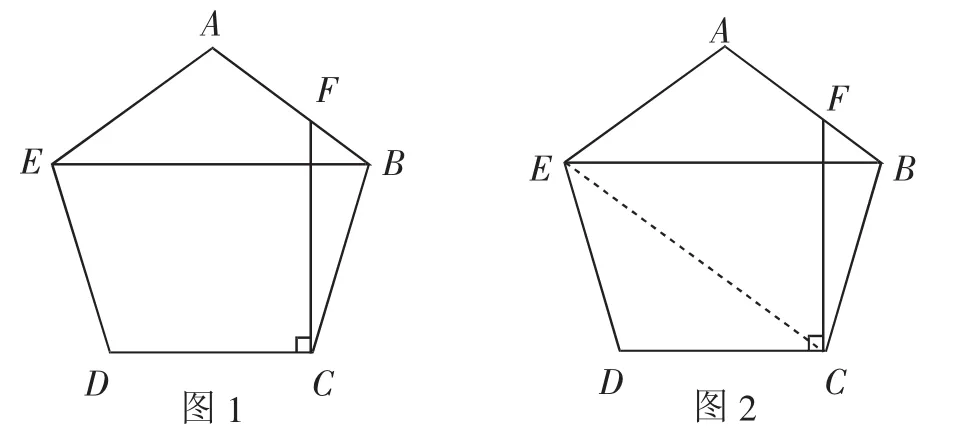
证明：如图2，在正五边形ABCDE中，AB=BC=CD=DE=EA，∠ABC=∠BCD=∠CDE=∠DEA=∠EAB=108°.

∠ABE=∠AEB=36°.

∠DEB=∠CBE=72°.

又∠DCF=90°，所以∠BCF=18°，∠BFC=54°.

连接EC，则有EC=EB，且有∠DCE=∠DEC=∠CEB=∠EBA=36°.

所以AB//EC.

所以∠ECB=∠EBC=72°.

所以∠ECF=∠BFC=54°.

说明：通过以上条件结论的梳理可以发现，在正五边形中，各边长相等，对角线长相等，添加辅助线后，还能够生成多个顶角为108°、72°、54°、36°的等腰三角形，这些条件在问题的证明过程中都可以充分利用.同时，要特别关注与AF相等的线段，这也是证明本题的关键所在.

二、两类六种证明

“截长补短法”是初中平面几何问题中一种常见的辅助线添加方法，也是一种证明平面几何问题的重要方法，其中蕴含着将几何问题化难为易的化归思想.下面，笔者就利用两类方法，即“补短法”和“截长法”给出六种问题的证明过程.

第一类：补短法.所谓“补短”，就是在两条短边中选择一条短边加以延长，使延长后所得新线段的长度等于长边的长.

证法1：如图3，延长EA与CF的延长线交于点P.

因为∠EAF=108°，∠AFP=∠BFC=54°，所以∠APF=54°=∠AFP.

所以AF=AP.

因为AF//EC，所以∠ECP=∠AFP=∠APF.

所以∠ECP=∠EPC.

所以EC=EP.

所以AE+AF=AE+AP=EP=EC=BE.

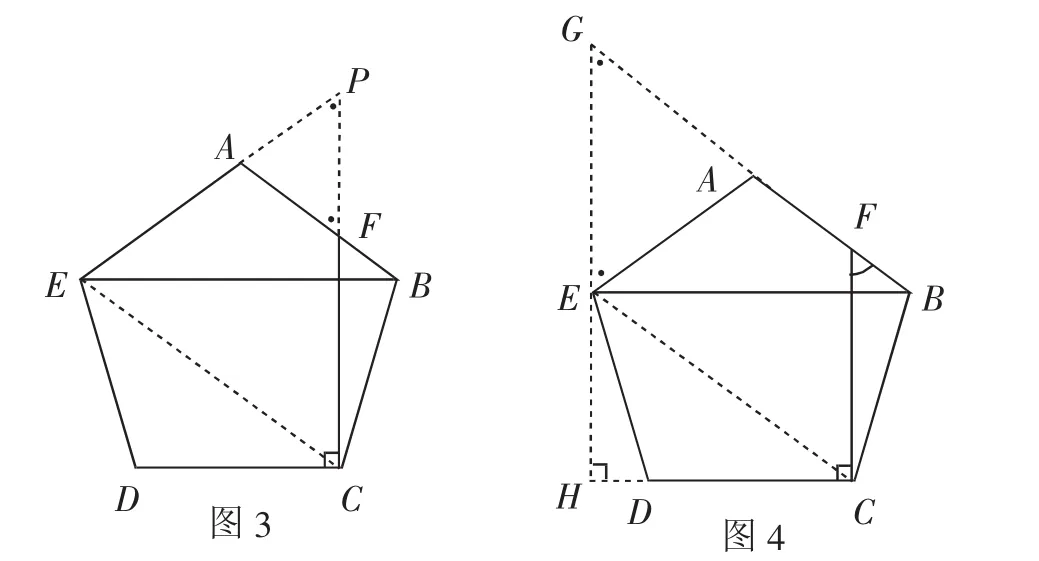
证法2：如图4，过点E作直线HG//FC，与BA的延长线交于点G，与CD的延长线交于点H.

因为BG//CE，所以四边形CFGE为平行四边形.

所以EC=FG.

注意到∠CFB=∠EGA=54°，因为∠EAB=108°=∠EGA+∠GEA，所以∠GEA=54°.

所以AG=AE.

所以AE+AF=AG+AF=FG=EC=EB.

证法3：如图5，过点C作CG//EA，与AB的延长线交于点G.

因为AB//EC，所以四边形AGCF为平行四边形.

所以AE=GC.

所以∠ECG=∠EAG=108°.

注意到∠BFC=54°=∠FCE=54°，所以∠GFC=∠GCF.

所以FG=GC=AE.

所以AE+AF=GF+FA=GA=EC=EB.

说明：从证法1到证法3，应用的都是“补短法”，构造等腰三角形是其中相同且核心的步骤.证法1中构造的是以AF为一腰的等腰△APF，证法2中构造的是以AE为一腰的等腰△AGE，证法3中构造的则是转化后的以GF（等于AE）为一腰的等腰三角形.虽然三种证明方法都需要添加辅助线，但是相对比较简洁、明快.

第二类：截长法.所谓“截长”，就是将长边（或与其相等的线段）截成两段，使截得的两条线段的长等于已知两条短边的长.

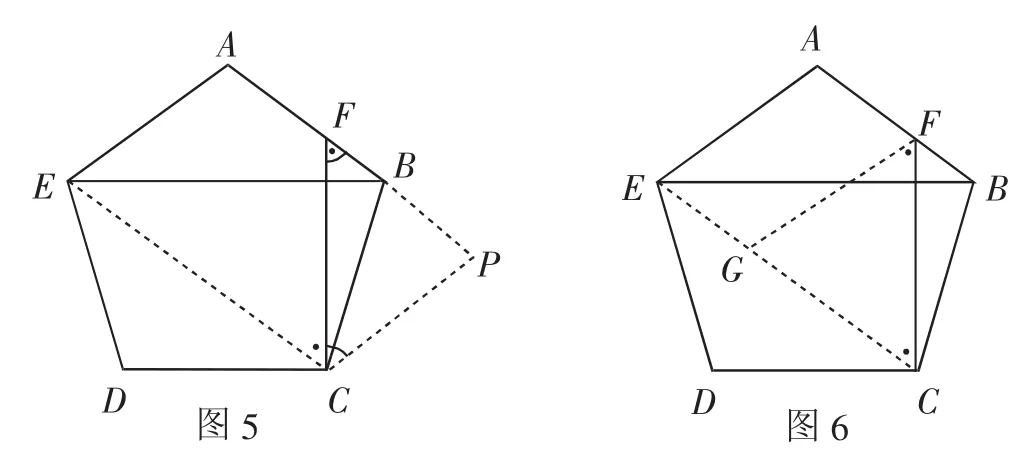
证法4：如图6，过点F作FG//AE，与EC交于点G.

所以四边形AEGF为平行四边形.

所以AE=FG，AF=EG.

所以∠EAF=∠EGF=108°.

所以∠FGC=72°.

注意到∠ECF=54°，所以∠GFC=54°，所以GC=GF=EA.

所以AE+AF=GC+EG=EC=EB.

证法5：如图7，过点A作AG//FC，与EC交于点G.

注意到AB//EC，所以四边形AGCF为平行四边形.

所以GC=AF，∠FCE=∠AGE=54°.

又∠AEG=∠AEB+∠CEB=72°，所以∠EAG=54°.

所以EA=EG.

所以AE+AF=EG+GC=EC=EB.

证法6：如图8，连接EC、BD，设交点为H.

根据正五边形的性质，则有EH//AB，BH//AE.

又因为AB=AE，所以四边形ABHE为菱形.

所以AE=EH.

连接AH，则有AH⊥EB.

又因为CF⊥EB，所以AH//FC.

又因为HC//AF，所以四边形AHCF为平行四边形.

所以HC=AF.

所以AE+AF=EH+HC=EC=EB.

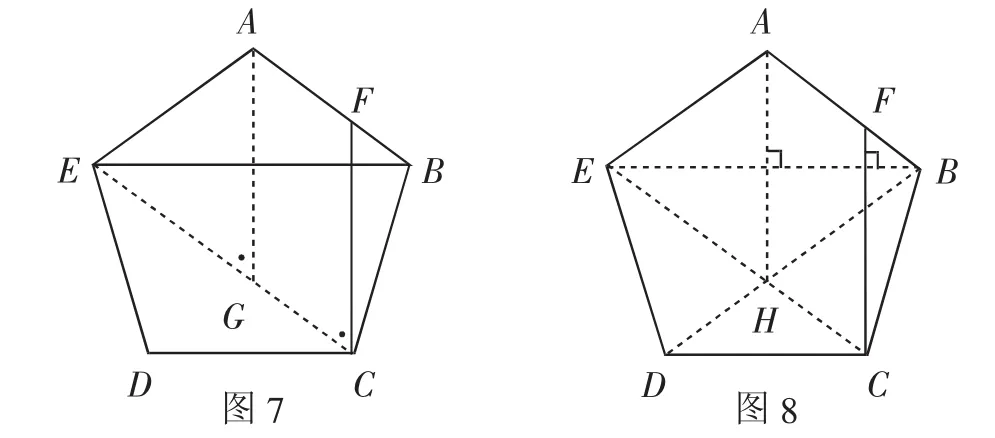
说明：从证法4到证法6，应用的都是“截长法”.证法4和证法5依然基于转化思想，在转化后构造了以AE为一腰的等腰三角形.证法6则独树一帜，简洁漂亮，证明过程一气呵成.首先，通过充分利用正五边形的性质，获得菱形AEHB；进而利用已知条件CF⊥EB，得到平行四边形AHCF，最终，殊途同归，应用与EB相等的对角线EC使问题得证.

回顾上述两类六种证明，我们可以看到，在问题证明的过程中，越是能快速利用已知条件，证明过程就越简单.事实上，证明越简单，也就越能反映数学问题的本质.同时，简洁的证明始终是数学推理的追求，简单化原则也是数学科学不断发展的生命.就像著名数学家丘成桐所说：数学家都希望用简洁的数学语言将这些自然现象的本质表现出来.因此，在数学教学中，教师也要有意识地培养学生这种不断追求、不断超越、永不服输、永不言弃的精神，这也是数学的精神.

三、教学启示

启示1：深刻认识平面几何教学的教育价值

美国数学教育家波利亚（G.Polya）对“为什么要进行几何证明”做过如下阐述：“如果一个学生不了解这个或者那个特殊的几何事实，并不要紧，因为在他以后的生活中，也许很少用到这些事实.但是，如果他没有学会几何证明，他就没学到真实论据的最好和最简单的例子，也错过了获得严格推理概念的最好机会.”［2］我国数学家王元院士认为：几何的学习不是说学完了这些知识有什么用，而是针对它的逻辑推导能力和严密的证明，而这一点对一个人成为一个科学家，甚至成为社会上素质很好的公民都是非常重要的.这个能力若能在中学里得到有效训练，会终身受益无穷.［3］

由此可见，平面几何问题的推理证明是培养学生创造性思维品质、发展学生逻辑推理素养和理性思维精神的有效载体.作为中学数学教师，应该十分重视并充分发挥平面几何教学的教育价值.

启示2：深刻认识添加辅助线的思维培养作用

解决平面几何问题常常需要添加辅助线，恰当、准确地添加辅助线，不仅可以使问题迎刃而解，还可以使问题的解决过程简化，论证表述简洁.事实上，添加辅助线的作用就是将内隐在问题中的几何图形的特征和性质外显出来，将题设条件和结论之间建立起逻辑关系，进而创造利用几何定理解决问题的条件，达到推证结论的目的.

因此，平面几何的教学要特别注重几何直观，要基于对几何图形特征的深入观察分析，引导学生展开想象，直觉或逻辑地提出一些问题解决的设想、联想或猜想，并以此为线索初步勾画出解决问题的方案，进而经过精细的逻辑加工得出问题的完整解答.［4］同时，在课堂教学中，教师要特别关注添加辅助线对培养学生思维品质的作用，不断引导学生追问添加辅助线的思路是如何想到的，认真指导学生回顾不同添加辅助线的思路对证明过程的影响，在回顾反思和对比研究的过程中驱动学生主动探究更加简洁的思路和简明的方法，从而促进学生不断梳理和掌握添加辅助线的一般思路和基本规律，深刻体会蕴含于几何问题解决过程中的数学思维之美、逻辑严谨之美和表达简洁之美.

启示3：深刻认识平面几何教学改进的意义

图形与几何是数学学习的重要内容，在课堂教学过程中，作为数学教师，要不断改进课堂教与学的方式，通过合理创设情境，引导学生认识图形的定义、理解图形的性质与判定，全程经历观察猜想、推理证明、得到结论的研究过程；通过精选几何问题，引导学生对问题的已知条件进行深入理解、适度演变，指导学生在探求几何图形本质、拓宽几何思维空间的过程中，理性认识动态几何图形在变化过程中的不变量或不变性；通过营造深度体验交流活动的时空，引导学生对几何问题证明思路的深刻分析和对证明过程的数学表达，指导学生学会把握几何问题中条件与结论之间的关联，促进学生掌握逻辑推理的基本形式，学会有逻辑地思考问题和数学地表达交流.

在平面几何教学中，教师要善于选材，要充分利用那些“有意义且不复杂”的题目去帮助学生发掘问题的各个方面，使得通过对这些问题的一题多证（解）、一题多问和一题多变等途径，引领学生深入挖掘几何图形的重要特征，深刻把握几何问题内在的数学本质，充分发挥几何问题内在的思维力量，驱动学生从多个角度探索解题的思路，促进他们系统把握平面几何的有关知识，学会利用科学、准确的数学符号语言和图形语言正确地表达逻辑思维过程.［4］

综上所述，在课堂教学中，教师要通过精良的几何问题，培养学生通过图形直观发现问题的几何特征，正确运用图形记号、数学符号语言和逻辑推理的方法表达平面几何中的演绎推理过程.这样做，便可将数学之大道自然融入问题的发现、提出、分析与解决的全过程之中，把学生获得解题能力的眼前利益和提升数学核心素养的长期利益有机融合起来，让学生通过“一道道门户”，走进一个完整的学习领域，体验探索发现的生命意义，切实发挥平面几何教学的育人价值.［5］