基于案例的“数学模型演绎”教学与反思

☉浙江省台州市黄岩区城关中学 林秋萍

建立模型思想能够帮助学生更好地体会数学和外部世界之间的联系，建构基本的数学模型、推广已有的数学模型、演绎更多的数学模型其实都是包含在模型思想范畴内的具体环节，教师有意识、有计划的训练能帮助学生获得以一当十的数学建模与演绎能力.本文结合具体的例题，对数学模型的演绎展开思考，以期促成学生创新意识的增强.

一、数学模型的演绎概述

个体因为内源、外源的需要，往往会产生建构模型的需要，以及模型建构的目标体系，在目标达成中进行有意义的加工与选择，并对已有模型进行反复分拆、重组与变化，直至新的符合目标要求的模型形成，以及新的知识经验的获得.由此可见，数学模型的演绎一般会经历“源驱动—已有模型—条件变换—建立新模型”这一过程.个体在已有模型的反复分拆、交叉、重组、变换中对模型进行存储、变换和重组，并因此顺利建构新的数学模型.

二、案例研究

例1 如图1，正方形ABCD的边长是4，E为AB边上一点，且AE=3，点Q是对角线AC上一动点，则△BEQ的周长最小应为______.

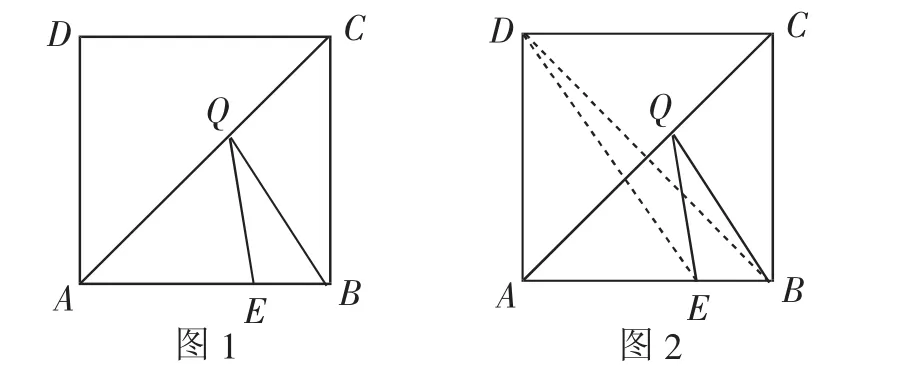
解题分析：因为EB为定值1，要求△BEQ的周长的最小值，也就转化成了求EQ+BQ的最小值，因此确定点Q的位置成为解决此题的关键.点Q在AC上，是运动的，EQ和BQ无法直接求得，所以联想对称性这一性质，并添加辅助线将EQ和BQ转化成一条线段并确定点Q的位置.如图2，正方形ABCD中，B、D两点关于直线AC对称，则DE的长即为EQ+BQ的最小值，利用勾股定理即可求得其值为5，则△BEQ的周长的最小值6很快求出.

模型演绎分析“：牧童饮马”这一问题是此题的模型原型，解决此题时应该明了正方形是本题的背景图，将正方形的一条对角线AC作为定直线，动点Q在对角线AC上，定点E、B在对角线AC同侧，正方形为轴对称图形等条件综合起来，即可利用对称性特点将“两线段之和”转化成“一条线段”.

例2 如图3，已知直线a、b，且a∥b，若a、b之间距离为4，点A至直线a的距离和点B至直线b的距离分别是2、在直线a、b上分别找出一点M、N，满足MN⊥a，并能令AM+MN+NB最小，此时AM+NB=______.

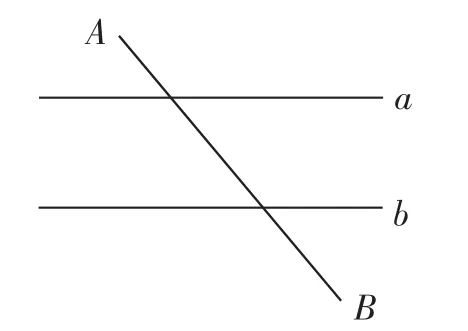
图3

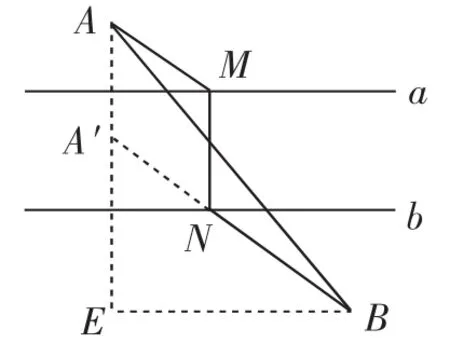
图4

解题分析：想要AM+MN+NB最小，MN为直线a、b之间的距离且为定值，因此，只要满足AM+NB的值最小即可解决问题，如图4，首先作点A关于直线a的对称点A′，连接A′B与直线b相交于点N，过点N作NM⊥a，连接AM，此时可判断出四边形AA′NM为平行四边形，因此可得AM=A′N，由两点间线段最短这一性质可得此时AM+NB的值最小.过点B作BE⊥AA′，与AA′相交于点E，在Rt△ABE中，求出BE，在Rt△A′BE中，求出A′B，即可求得AM+NB.

模型演绎分析：平行线是解决此题时所运用的背景图，a、b为定直线，M、N两动点分别在定直线a、b上，由题意可得A、B两定点在定直线a、b的两侧，以定直线a或b为基础确定动点N或M并因此构建“牧童饮马问题”的模型，利用对称性、平行四边形等性质将问题进行转化，即可寻得此题的突破口.

三、几点思考

1.重视模型建构和演绎

一种数学形式向另一种形式的转化，实际上正是数学杠杆在起作用的过程，作为数学思维支撑点的数学模型同样是数学知识的附着点及数学应用的突破点.学生对数学模型进行观察、归纳、类比与思考，往往需要对数学模型中承载的数学信息进行获取、分析、归纳与综合，数学学习的核心活动也正在于此.教师应看到学生建构模型在数学学习活动中产生的价值，着眼于学生思维发展设计出适合学生能力与水平的数学模型，帮助、指导学生对模型进行理解、表征、建构，并在此基础上进行数学操作与推理.因此，数学教育、模型构建、模型演绎应被有机结合并落实到具体的数学操作与推理中，教师应着眼于学生模型构建意识的培养，并不断引导学生应用数学知识和方法进行观察、分析与解决，使学生能够在实际问题的分析与解决中，积极构建认知结构，并因此由知识型向能力型转变.

2.正确处理模型构建和演绎之间的关系

在具体数学模型的建构过程中，第一步应要求学生从现实生活、具体情境中进行数学问题的抽象，第二步则要求学生运用数学符号对问题中的数量关系、变化规律进行表达，方程、不等式、函数等都是一般的表达方式.先直观后逻辑是数学模型建构必须遵循的过程，这是一个需要运用逻辑检验、驾驭数学直觉的阶段.对数学模型进行反复分拆、交叉、重组、变换的演绎过程应建立在客观事物的数学抽象与已有模型之上.值得教师注意的是，这两者既不是“母子关系”，也不是很多学生误解的“包容关系”，事实上，数学模型的建构和演绎应该说是一种“基础和拓展”的关系，已有数学模型或原有图式是演绎新模型的基础，新模型的演绎是已有模型或原有图式的拓展，具备一定层次关系的模型链和模型系统由此建立.

3.教学注意

（1）数学逻辑和直觉相结合

将数学模型建构和演绎之间的“基础和拓展”关系进行简单的套用是无法令学生理解和掌握的，教师在实际教学中，应将数学直觉和逻辑、合情推理和逻辑推理结合起来，并引导学生逐步进行模型的分拆、变换与重组.对模型的直观想象、分拆、重组、变换是数学直觉对数学信息进行加工的重要阶段，对模型形成进行逻辑检验与建构关系的过程则是数学逻辑参与的重要阶段.因此，教师在实际教学中，应引导学生进行充分的直观感知，并进行分拆、重组与变换操作，使学生能够在观察、归纳、类比中建构模型特征与模型之间的猜想、合乎逻辑的理性思考与检验、模型的修改等数学操作.

（2）做到循序渐进

学生思维发展的高度价值往往在数学模型的建构和演绎活动中得以完全展现，数学直觉和逻辑并用、合情推理和逻辑推理有机融合才能令学生在数学活动中展现出更高层次的思维活动与个性化想法.学生在数学活动中的深度参与和积极思考，才能令数学活动展现出高层次思维参与的价值与魅力.因此，教师不能对建构数学模型抱有“一步登天”的妄想，而应该循序渐进地设计出适合学生的模型建构和演绎活动，以帮助学生达成深层次的思考.不仅如此，任何模型的建构和演绎都需要基础模型的支撑，这是教师需要关注的，因此，教师应尽量启发学生在基础模型的建构与掌握中形成更多、更丰富的体验，使学生能够在自身认知基础上，结合更多个性化的想法顺利从模型的建构向演绎过渡，使学生能够在直观感知与已有经验的结合中，顺利实现逻辑建构，并实现合情推理和逻辑推理的综合运用.

（3）注重动态生成

适合学生的模型建构与演绎活动往往能令学生思维品质的灵活性、创造性，以及智力、能力都获得发展.不过，强制要求学生记“模型”、背“模型”的做法是极不合适的，这种“模型化”的机械操作往往无法令学生对模型建构与演绎之间的联系产生深刻的领会和感悟.因此，教师要清楚认识已有数学模型多元表征的含义与价值，并引导学生在此基础上进行新模型的分拆、变换与重组，使学生能够不断获得新知识与新观念，并在模型构建与演绎的活动中展现出令人惊喜的潜能.