烧蚀型脉冲等离子体推力器能量分配机理
2018-11-19,,,,
,,,,
1. 上海航天控制技术研究所,上海 201109 2. 上海市空间智能控制技术重点实验室,上海 201109 3. 北京理工大学 宇航学院,北京 100081
作为最早应用于航天任务的电推力器,脉冲等离子体推力器[1](Pulsed Plasma Thruster,PPT)具有比冲高、结构简单、控制方便灵活、能在低功率下稳定工作等特点,可以满足小卫星,尤其是质量小于100 kg的小卫星对系统提出的低功耗和低质量等严苛要求。PPT最早在1964年由前苏联在星际探测器Zond-2[2]上首次使用,目前已成功应用于位置保持、姿态控制以及轨道转移等十余次在轨推进任务[3-5]。近年来,PPT仍然是电推进系统发展的重要方向[6-8]。
虽然经过了五十多年的研究,并且已成功应用于空间飞行器,PPT仍存在一系列的理论和应用问题有待研究和解决。长期以来,PPT为人所诟病的问题是其效率低下,研究结果表明,现有绝大多数型号的PPT的效率均低于10%,低功率PPT的效率甚至只有3%左右[9]。
为了提高PPT的效率,研究者们进行了大量实验,研究PPT的放电能量[10]、几何参数[11]以及电路参数[12]对PPT推进性能的影响,以探索提高PPT效率的方法,但PPT的效率依然较低。要提高PPT的效率,必须深入研究PPT的能量分配规律,探索减少PPT能量损失的方法,把更多的能量分配到喷出工质的有效动能上。
过去对于PPT能量机理的研究匮乏,仅有美国伊利诺伊大学的Rodney L.Burton对PPT工作过程中的能量平衡和效率进行过分析[13]。但研究仅从工程角度,通过一些PPT样机的实验数据估算PPT的能量损失比率,并未从物理角度深入探索PPT的能量分配机理。
近年来,某些PPT研究者另辟蹊径,考虑从改变PPT能量释放方式的途径提高其效率,将PPT能量分配到多个电容上在不同时间或空间上通过多次放电释放[14-15]。但由于缺乏理论指导,目前并未取得突破性成果。
本文从能量分配的角度研究PPT放电过程中的能量损失,理论地分析PPT效率低下的原因。并以平板式烧蚀型脉冲等离子体推力器为研究对象,通过测量其放电电压、放电电流、烧蚀质量等参数,估算其元冲量、比冲、效率等推进性能。结合数值模型,分析实验结果,总结PPT工作过程中的能量分配规律。
1 PPT的能量分配机理分析
对于PPT系统而言,总效率涉及到电源效率和推力器效率,由于PPT的电源效率通常能达到80%~93%[13],所以PPT效率低下的原因是推力器效率低下。本文用ηt来代表推力器效率,PPT的推力器效率通常用下面公式计算:
(1)
式中:m为PPT单次放电烧蚀掉的推进剂质量;v为由元冲量计算得到的喷出工质平均速度;E0为电容放电能量;Ibit为PPT的元冲量,即单次工作所产生的冲量。
若电源效率ηc一定,式(1)可以写成:
(2)
式中:T为推力器的平均推力;Isp为比冲;g为重力加速度。由式(2)可以看出,推力器效率实际是和推力功率比与比冲的乘积成正比的一个物理量,推力效率越大,电推力器的比冲和推力功率比的乘积越大。
但要注意的是,当喷出工质速度不相同时,喷出工质的动能应由下式计算。
(3)
对于PPT,由于喷出工质的成分很复杂,有不同的离子和中性粒子,故PPT的喷出工质速度分布范围很大,过去的研究成果表明[8],PPT喷出的高速离子的速度能超过20 km/s,而喷出的低速中性气体的速度低于5 km/s,甚至有的只有300 m/s。所以用PPT的推力器效率无法直接反映电容能量的转换效率。
本文将PPT电容能量转换为喷出工质有效动能的效率称为PPT的能量利用率。所谓有效动能,指的是对产生推力有贡献的动能。文献[2]表明,PPT喷出工质的速度并不完全垂直于喷口,平行于喷口截面的冲量分量对产生推力无贡献。能量利用率ηe由式(4)计算:
(4)
由上述分析可知,对于PPT而言,当放电烧蚀的工质全部电离且喷出速度一致时,推力器效率等于能量利用率。下面用LES-6的PPT的实验结果来证明,在不同的能量利用率下,推力器效率也可能会相同。
LES-6[8]上使用的PPT的放电能量为1.85 J,实验测得的元冲量约为30 μNs,单次放电的烧蚀质量约为10 μg。故比冲为300 s,即喷出工质的平均速度为3 000 m/s,推力器效率约为2.4%。根据喷出粒子速度的测量结果[9-10],喷出的离子的速度在30 km/s左右,中性粒子速度大约在300~5 000 m/s。假设该PPT喷出的等离子体和中性气体的速度一致且方向都平行于极板,等离子体速度为vi,则在中性气体速度为vg时,有如下关系式:
(5)
设vi=30 km/s,vg=300 m/s、1 000 m/s和2 000 m/s时,能量利用率如表1所示。
可见,喷出工质的速度越接近,能量利用率和推力器效率越接近。由于PPT的喷出工质的速度分布情况过于复杂,故无法通过实验手段获得PPT的能量利用率,给研究PPT能量分配机理带来非常大的困难,故需要进行相关假设。
表1 LES-6的PPT的速度分布情况与能量利用率的关系
Table 1 Relation between the velocity distribution and the
energy utilization in the PPT of LES-6

中性气体速度/(m·s-1)等离子体质量/μg中性气体质量/μg能量利用率/%20000.369.649.810000.699.3117.03000.909.1021.9
下文中,由于中性气体的喷出速度低,对推力的贡献可以忽略,故假设中性气体喷出速度为0,同时还假设喷出等离子体的喷出速度相等,则有:
(6)
ηp为PPT的推进剂利用率,即烧蚀出的工质能电离成等离子体的比率。在上述假设下,PPT的推力器效率等于能量利用率和推进剂利用率的乘积。
2 研究方案
2.1 实验方案
本文以经典的平行板型脉冲等离子体推力器为研究对象,通过实验分析样机的能量分配规律。推力器参数如表2所示。

表2 PPT样机设计参数
本文选用750 V、1 060 V、1 300 V和1 500 V(能量比为1:2:3:4)的放电电压。推力器在上述4种工况下工作500次,测量推力器的放电电压、放电电流和总推进剂烧蚀量。其中,放电电压由安捷伦10 076 B高压探头(最大输入4 000 V,带宽250 MHz)测量,放电电流由罗柯夫斯基线圈(量程为10 mA~500 kA,采样频率10 MHz)测量,总烧蚀质量由赛多利斯CPA225D型高精度电子天平(精度0.01 mg)测量。
通过计算,获得推力器的元冲量、比冲、效率等推进性能参数。
元冲量由下式估算。
(7)
得到元冲量后,由下式计算比冲:
(8)
本研究利用称量500次放电的总烧蚀质量求平均值的方法来获得m。
由于本文不考虑电源效率,故忽略电源能量损失,则推力器的推力功率比为:
(9)
由于本文需要分析PPT的能量分配机理,所以必须要获得推力器的推进剂利用率。然而该参数很难靠实验获得,需要借助数值仿真手段。
2.2 数值模型
本文参考文献[16]中PPT烧蚀过程的建模方法并借鉴气体放电领域[17]的研究成果,假设极板间电场强度和中性粒子数密度分别与放电电压和电流相关,当两者满足一定关系时,此时刻烧蚀出的中性气体被电离成为等离子体。模型能估算PPT推进剂利用率和生成的等离子体质量,并结合实验数据获得能量利用率。流程如图1所示。
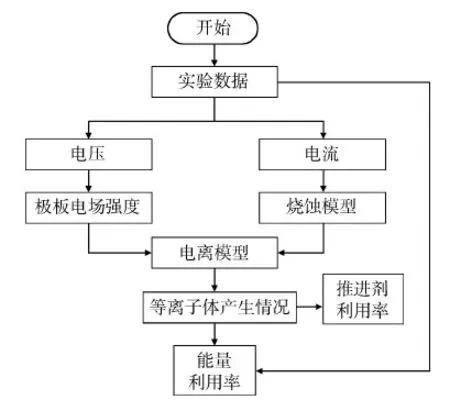
图1 数值模型流程Fig.1 Flow chart of the simulation model
由于PPT推进剂烧蚀机理极其复杂,目前仍然没有模型能够准确的模拟PPT工作时中性气体的产生过程。故本模型参考文献[16],对PPT的推进剂烧蚀过程进行简化,假设PPT推进剂烧蚀全部发生在PPT放电过程中,中性气体进入放电区域(极板间)的流量与电流的平方成正比。此外,还假设新生成的中性气体会集中在一起,形成一片密度均一的中性气体片。则在t时刻,新进入极板间的中性气体片的质量为:
(10)
式中:mn为t=n·Δt(n=1,2,3,…,N-1)时刻进入放电区域的中性气体片的质量;m为单次放电推进剂烧蚀的总质量;N为时间步数;Δt为时间步长,本文中,Δt=10-9s。事实上,PPT工作过程中,固体推进剂的烧蚀速率并不与电流的平方成严格的正比关系。但推进剂的烧蚀和其获得的热量有关,而热量的来源为欧姆加热,与电流的平方正相关,故这个假设有一定合理性。
由于PPT常用的推进剂为聚四氟乙烯(PTFE)。根据实验研究结果[9],PPT工作时产生的等离子体中,碳离子和氟离子占的比重最大。所以本模型中,假设中性气体片由碳原子和氟原子组成,碳原子和氟原子均匀的分布在气体片中。则中性气体片的粒子数密度由式(11)计算:
(11)
式中:MC2F4为聚四氟乙烯的分子量;NA为阿伏伽德罗常数;w和h分别为极板的宽度和高度;δ为中性气体片的厚度,由下式计算:
δ=vg·Δt
(12)
假设极板间电场强度E(t)由下式计算:
(13)
则在t=n·Δt时刻,新进入放电区域的中性气体片中,电子与中性原子的平均碰撞能量为:
(14)
式中:q为电子的电荷量;λn为中性气体片中,电子和中性原子碰撞的平均自由程。λn由下式计算得到:
(15)
式中:rC和rF分别为碳原子和氟原子的半径,在本文中,取rC= 91 pm,rF=71 pm。
碳原子和氟原子的第一电离能分别为10.6 eV和16.5 eV。故本模型假设中性气体片的平均第一电离能为14.5 eV(2个碳原子和4个氟原子的第一电离能的平均值),当电子与中性原子的平均碰撞能量超过14.5 eV时,达到电离条件,中性气体片被电离为等离子体片。
用上述模型估算LES-6[9]上PPT的推进剂利用率,仿真结果为9.5%,与实验结果的10%接近。用模型估算美国XPPT-1实验样机[18]的推进剂利用率,结果为62.8%,与实验结果的60%相近。故模型可以用来估算PPT的推进剂利用率。
3 结果与分析
PPT在放电电压为750 V、1 060 V、1 300 V和1 500 V时,电流和电压曲线分别如图2~图5所示。

图2 初始电压为750 V时,PPT放电过程中电压和电流波形Fig.2 The voltage and current waveforms of the PPT discharge under 750 V initial voltage
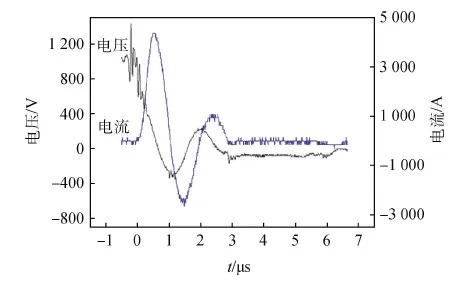
图3 初始电压1 060 V时,PPT放电过程中电压和电流波形Fig.3 The voltage and current waveforms of the PPT discharge under 1 060 V initial voltage
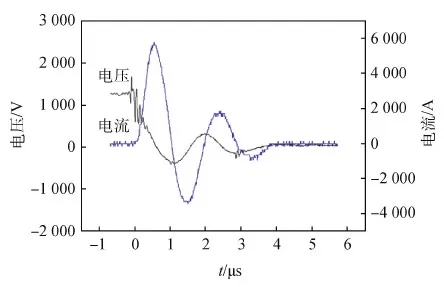
图4 初始电压1 300 V时,PPT放电过程中电压和电流波形Fig.4 The voltage and current waveforms of the PPT discharge under 750 V initial voltage
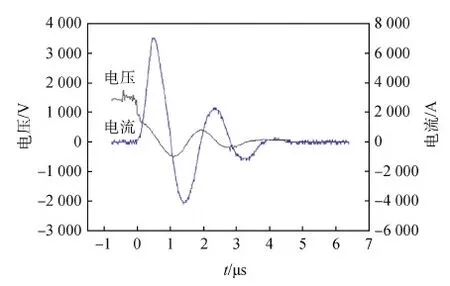
图5 初始电压1 500 V时,PPT放电过程中电压和电流波形Fig.5 The voltage and current waveforms of the PPT discharge under 1 500 V initial voltage
从图2~图5可以看出,随着放电能量的增加,PPT放电时间延长,放电电流峰值升高。
利用2.1中的经验公式,获得不同初始电压下,PPT样机的元冲量、推力功率比、单次脉冲烧蚀质量、比冲和推力器效率。结果如图6~图10所示。

图6 4种不同初始电压下的元冲量Fig.6 Impulse bits for four different initial voltages
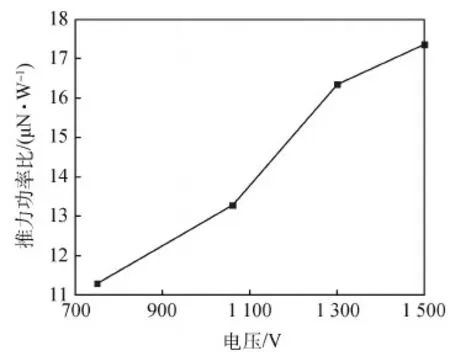
图7 4种不同初始电压下的推力功率比Fig.7 Thrust power ratios for four different initial voltages
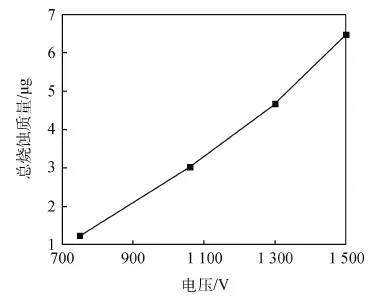
图8 4种不同初始电压下的总烧蚀质量Fig.8 Ablated masses for four different initial voltages
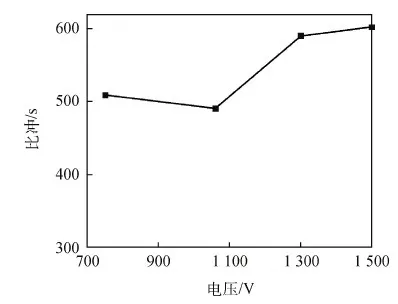
图9 4种不同初始电压下的比冲Fig.9 Specific impulses for four different initial voltages
由图6~图10可知,当PPT极板间距和储能电容值为定值时,随着电容电压和放电能量的增加,推力器的元冲量、推力功率比、单次放电的烧蚀质量和推力器效率都增加,而比冲则是先下降后上升。元冲量由6.36 μNs逐步升高至39.06 μNs,推力功率比由11.31 μNs/W逐步升高至17.36 μNs/W,单次放电烧蚀质量由1.25 μg逐步升高至6.48 μg,推力器效率由2.88%逐步升高至5.23%。比冲则是先从509 s降至491 s,之后逐步升至602 s。

图10 4种不同初始电压下的推力器效率Fig.10 Thruster efficiencies for four different initial voltages
根据PPT工作机理,随着放电总能量增加,用于推进剂电磁加速和烧蚀的能量也增加,从而使PPT的元冲量和单次放电烧蚀质量上升。比冲与工质平均喷出速度成正比,推力功率比则与工质烧蚀及加速同时相关,其变化规律需要借助等离子体诊断技术和温度测量技术开展进一步分析[19]。
而效率的变化,需要借助数值仿真模型进行分析。根据数值模型,估算得到的推进剂利用率和能量利用率如图11所示。
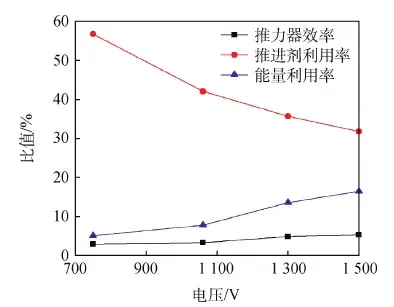
图11 4种不同放电电压下的能量利用率与推进剂利用率Fig.11 Energy utilizations and propellant utilizations for four different initial voltages
理论估算结果显示,PPT极板间距和储能电容容值为定值时,随着电容电压和放电能量的增加,能量利用率增加,但推进剂利用率下降。能量利用率和推力器效率分别由5.07%和2.88%逐渐提高至16.46%和5.23%,推进剂利用率则由56.8%逐渐降低至31.8%
这一结果表明,提高放电电压和放电能量有利于增加PPT的能量转换效率,将更多能量用于电磁加速。但另一方面,由于PPT放电能量分配不可控制,当总放电能量提高时,用于推进剂烧蚀的能量也同时提高,将有更多推进剂被烧蚀,导致极板间中性气体密度增加。根据气体放电理论,中性气体电离度跟气体密度反相关,与极板电压正相关,故放电能量和电压同时增加的情况下,有可能导致推进剂利用率反而下降。按本文研究结果,推进剂利用率反而降低,具体原因将在后续研究中探索。而根据第2节中的理论分析,PPT的推力器效率与能量利用率和推进剂利用率同时相关,增加放电能量主要是通过提高能量利用率的途径提高推力器效率。
4 结束语
本文针对PPT效率低下的缺点,对PPT的能量分配规律进行研究。以一个经典平行板式PPT为对象,通过实验和数值仿真的手段,探索其在不同放电电压和能量下工作时,能量利用率、推进剂利用率和推力器效率的变化规律。结论如下:
1) PPT的推进性能与放电能量相关,在极板间距和储能电容容值为定值,随着放电能量增加,元冲量、推力功率比、单次放电的烧蚀质量和推力器效率都增加,而比冲则是先下降后上升。
2) 元冲量和单次放电烧蚀质量随放电能量的增加的原因是PPT用于电磁加速和推进剂烧蚀的能量增加。
3) 能量利用率和推进剂利用率低下同时导致PPT推力器效率低下,随着放电电压和能量的增加,PPT的能量利用率和推力器效率上升,但推进剂利用率反而降低。
4) 增加放电能量主要是通过提高能量利用率的途径提高推力器效率。但由于增加放电能量的同时提高了推进剂烧蚀质量,有可能导致推进剂利用率反而下降。
5) 后续需要从实验和数值仿真两方面开展更深入的研究。实验方面,需进一步开展等离子体速度和组分、推进剂表面温度、磁场分布等物理参数的测量工作,将PPT能量分配情况进行细化。数值仿真方面,需对现有模型进行改进以提高准确性。
