固体微型推力器应用设计
2012-12-29刘旭辉陈君魏延明汪旭东
刘旭辉 陈君 魏延明 汪旭东
(北京控制工程研究所,北京 100081)
1 引言
卫星微型化是今后一个重要的发展方向,微型化也带来了一定的挑战,皮纳卫星上难以携带常规的轨道控制动力系统,基本处于无控状态,其利用价值大大降低。而固体微型推力器阵列体积小、集成度高、功耗低、可靠性高[1-2],能够提供小而精确的冲量,可以作为微型卫星的执行机构,是一种新型的卫星控制动力装置,可以进行高精度的姿态控制和轨道控制,能够大大提升微型卫星的实用价值[3-4]。
现阶段从事微推进系统的研究机构众多,但各研究机构主要集中在对推力器的结构设计、性能试验和仿真分析等方面的研究,基于推力器阵列与布局设计的研究国内外研究较少,但是现阶段采用正四边形的推力器阵列方式,无法保证每组推力器组合的合力通过卫星质心方向,不能满足轨道控制的需要[5-6],须要设计一种满足姿轨控的推力器阵列方法。
本文主要就推力器的阵列设计以及阵列布局设计进行分析研究,提出了正六边形为基元的推力器阵列方式,对正六面体的推力器阵列布局进行了相关分析,可为固体微型推力器阵列的应用奠定一定基础。
2 推力器阵列设计
2.1 固体微型推力器阵列工作特点
固体微推力器阵列中每个推力器单元只能使用一次,单个推力器冲量一定,通过选择不同数量的推力器组合,或者选择不同力臂的推力器来实现轨道和姿态的精控粗控,易于形成多种控制档次。推力器阵列需要能够满足轨道控制和姿态控制,而现有的推力器阵列方式采用正四边形为基元扩展而成,不能满足轨道控制的需要,不能保证每次选择的推力器组合均能通过卫星质心方面,因此需要对其进行设计。
推力器阵列布局方式对于姿态控制要求较低,而对于轨道控制需要合力通过卫星质心方向,并且需要推力器阵列布局具有较好的规律,便于进行寻址点火。
2.2 推力器阵列设计方法
根据控制要求,设计了一种新型的推力器阵列布局方式(图1),基准生成图形为正六边形,按照式(1)进行扩展,即按照相邻推力器间距相等的原则,生成其他推力器的位置,最终扩展出所需的阵列。

式中:rα、rβ为相邻两个推力器的位置矢量,dcon为给定值。

图1 推力器阵列Fig.1 Thruster array
如图1所示,中心颜色加深的正六边形为基准图形,设此正六边形基元外接圆的半径为RH,向外不断扩展的推力器依然分布于外接圆半径分别为2RH,3RH,…,nRH(n∈N)的正六边形上。同样,如果按照相邻推力器间距相等的原则生成整个阵列,则中心基元为正六边形,该种布局方式具有唯一性。
最终确定的推力器阵列基本原则为:①以正六边形为基元;②每个相邻推力器间距相等。将本设计方法命名为“正六边形基元法”。
2.3 正六边形基元的优点
(1)从几何学角度讲,正六边形具有更好的对称性,无论选择偶数个推力器还是奇数个推力器进行组合,都能够保证产生的合力通过圆心;正六边形的边长等于其外接圆半径,便于求解出推力器的位置。相邻推力器间距相等,扩展出其他的推力器仍然布局在外接圆半径更大的正六边形上,使推力器容易进行选择组合。
(2)从拓扑学的角度看,正六边形具有更好的连通性,增强了不同区域间推力器的联系,且结构紧凑有规律,容易找出规律,利于姿轨控推力器分配算法的设计。
(3)以正六边形为基元的推力器阵列相对于正四边形的可以有效提高单位面积上推力器的数量,布置相同数量的推力器能够节省一定的卫星表面使用面积。
2.4 正六边形阵列设计的特点
按照正六边形基元法生成的推力器阵列不但能够满足卫星姿态控制和轨道控制的要求,而且具有较强的规律性,利于进行推力器分配算法设计。
如图1所示,将正六边形基元的外接圆命名为基准圆,将与正六边形边相交并且有两个交点的圆命名为正六边形的割圆。
由图1可知,所有的推力器均分布在某一半径上的圆上,并且每个圆上的推力器个数为6个或12个。外接圆半径为2RH的正六边形上的推力器分布在两个同心圆上,一个是正六边形的外接圆,一个是正六边形的内切圆;外接圆半径为3RH的正六边形上的推力器分布在正六边形的外接圆和正六边形的割圆上,外接圆半径为4RH的正六边形上的推力器分布在正六边形的外接圆、割圆以及内切圆上。依照该方法,生成的推力器均处于外接圆半径为2kRH或(2k-1)RH的正六边形上(k∈N),同时所有的推力器分布于基准圆的某个同心圆上。
由图1及以上分析可知,向外扩展的正六边形上的推力器所在的同心圆分为三种圆:正六边形的外接圆;正六边形的内切圆;正六边形边的割圆。外接圆、内切圆上推力器个数为6 个,割圆上推力器的个数为12 个。对于不同外接圆半径的正六边形,正六边形的外接圆、内切圆及割圆的数量存在一定的规律性;在每种外接圆半径下各个圆上的推力器分布个数也具有一定的规律性,具体分布规律如表1所示。

表1 推力器数量分布规律Table 1 Distribution of thruster number
当外接圆半径为2kRH时,推力器的个数为12×k2+6×k。当外接圆半径为(2k-1)RH时,推力器的个数为12×k2-6×k。假设k=15,外接圆半径为29RH,则阵列外接圆的个数为29个,内切圆的个数为14个,割圆的个数为196个,其他推力器没有分布在整圆上。共有推力器个数为29×6+14×6+196×12,即2610个。
2.5 应用性分析
对于基于推力器阵列的卫星控制,当仅进行姿态控制时,根据所需的冲量矩,推力器成对组合,冲量方向相反,抵消对轨道控制的影响,仅保留对姿态角速度的影响。
而仅进行轨道控制时,将推力器阵列圆周上推力器进行分组,每6个推力器为一组,由表1提供的推力器分布规律,容易进行推力器分组。将圆周上推力器个数为12个的分成2组,圆周上推力器个数为18的分为3组,每组相邻推力器间构成60°夹角。设单个推力器的冲量为Ⅰmin,当需要2Ⅰmin时,需要两个推力器角度间隔180°;当需要3Ⅰmin时,3 个推力器需要两两间隔120°。对于所需偶数个推力器可以按照组合产生2Ⅰmin的方式,对于产生小于6Ⅰmin冲量的情况,要分别处理,如果点1个推力器,则需要相对两个推力器阵列组合产生,一个点2个推力器,另一个相对的阵列点3个推力器;如果点5个推力器,则需拆成2 个和3 个组合产生;产生1Ⅰmin浪费的推力器太多,因此,除了1个推力器之外,其他余数按照7来计算,产生7Ⅰmin冲量时,则分成3Ⅰmin和4Ⅰmin的组合,由一个阵列提供即可。依据以上的组合规则进行组合,根据阵列的使用情况,提供轨道控制所需的冲量。
3 推力器阵列在皮纳卫星上布局设计
阵列安装需要满足姿轨控的要求,并且通常以能够提供较大的冲量矩为标准来设计阵列的安装方式。
设O-XoYoZo为星体坐标系,原点O在卫星质心,Xo、Yo、Zo三轴为卫星的惯量主轴,将推力器阵列所在坐标系a-XaYaZa命名为“阵列坐标系”,原点a为阵列中心,推力冲量方向与aXa轴一致,安装时,aXa通过卫星质心方向。设ea=[eaxeayeaz]T为阵列坐标系的三个基本矢量,该阵列安装时垂直于XaaYa面,设阵列与Oa夹角为ϑj,如图3所示。当仅产生冲量矩时,推力器以成对的方式进行组合,因此产生绕垂直于冲量方向与卫星中心O构成的平面的控制轴的冲量矩,设控制轴为Ol,该轴正方向垂直于XaaYa向外。如图2(a)所示,第j个阵列中第i个推力器的冲量矢量在阵列坐标系中为Iaji,推力器阵列-Ya平面内,第i-个推力器在阵列坐标系中的坐标为rji- =(xi-,yi-,zi-)ea,该推力器的冲量为Iji-;+Ya平面内,第i+个推力器在阵列坐标系中的坐标为rji+=(xi+,yi+,zi+)ea,该推力器的冲量为Ⅰji+。Rji-、Rji+分别为Iji-、Iji- 在O-XoYoZo坐标系中的矢量位置;rjo为a在O-XoYoZo坐标系中的矢量位置。

图2 构形设计Fig.2 Configuration design
设MI为冲量矩,同一阵列中所有推力器的冲量方向相同,位置不同。对于位于-Ya平面内的推力器要求其产生绕Ol轴负方向的冲量矩MIji- ,而位于+Ya平面内的推力器要求其产生绕Ol轴正方向的冲量矩MIji+,以-Ya平面内产生的冲量矩为例进行分析。

同理可得:

由冲量矩方向要求可以确定ϑj取值范围:
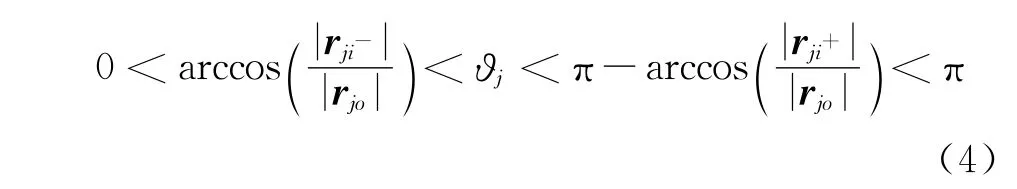
对于|MIji-|和|MIji+|,当推力器位置确定后,大小与ϑj有关,因此将所有推力器冲量矩能够同时取得较大值作为优化目标。
可以得出,rjO⊥YaaZa时,即推力器阵列与阵列中心在星体坐标系中的矢量方向垂直时,推力器阵列对卫星的冲量矩能够取得最大值。根据该关系,本文设计采用正六面体构型方式布置阵列,如图3所示,在六个面上各布置一个阵列。

图3 阵列布局Fig.3 Array configuration
假设进行六维控制任务,包括三维轨道控制,三维姿态控制,各个控制向量的阵列分配可以采用如表2所示的方案进行,阵列分配方案不是唯一的。

表2 控制向量阵列分配Table 2 Control vector allocation
4 包络面绘制
在各个推力器阵列的冲量和冲量矩输出范围内,所有推力器阵列所能输出的冲量和冲量矩的集合即为推力器配置的可达集,可达集的边界即为包络面,由包络面能够确定推力器阵列配置的控制能力[7-11]。
4.1 冲量包络面绘制
设Ⅰmin=1×10-3N·s,每个阵列中用于轨道控制的推力器个数为kc,因此三轴的冲量范围可以表示为

式中:1≤nc≤kc,nc为冲量个数;ⅠXo,ⅠYo,ⅠZo分别为Xo,Yo,Zo三个方向的冲量。
对于大规模推力器阵列包络面上节点过多,无法研究分析其特点,设每个阵列上用于轨道控制的推力器个数kc=25,绘制冲量的包络面。如果推力器阵列仅仅在轨道控制中的两个方向产生作用,以控制Xo方向和Yo方向为例,总共布置四个阵列:1号阵列、2号阵列、3号阵列、4号阵列,则包络面为二维平面,如图4(a)所示。如果为三向控制,布置六个阵列,即在Xo、Yo、Zo方向都安装阵列,则包络面为正六面体,如图4(b)所示。
4.2 冲量矩包络面
设推力器阵列中相邻推力器间距Lmin=2mm,MImin=Ⅰmin×Lmin=2×10-6N·s·m,MImin表示最小单位冲量矩。每个阵列能够提供kt单位冲量矩,三个方向的冲量矩范围为


图4 冲量包络面Fig.4 Impulse envelope
式中:1≤nt≤kt,nt表示冲量矩个数;MIXo,MIYo,MIZo分别为绕三个惯量主轴Xo,Yo,Zo的冲量矩。
以单个阵列能够产生最大kt=25单位最小冲量矩进行姿态控制为例,如果仅仅安装四个阵列即1~4 号阵列,则产生二维包络面,如图5(a)所示。如果安装六个阵列在正六面体表面上,则将产生三维包络面,如图5(b)所示。
由图4和图5可知,当各个阵列都提供相同的冲量和冲量矩时,以正六面体方式布置六个阵列,冲量和冲量矩的包络面为正六面体,最大控制能力由各个阵列的最大冲量和冲量矩决定,而控制精度由阵列能够提供的最小冲量和冲量矩决定,可以根据不同的任务需要设计相关推力器的性能,配置各个阵列的规模。


图5 冲量矩包络图Fig.5 Impulse moment envelope
5 小结
(1)研究了固体微型推力器阵列中推力器的设计方法,设计了适用于航天器姿轨控的正六边形基元的推力器阵列,分析了其优点及其应用性。通过该方法设计的推力器阵列能够满足轨道控制时,每组推力器组合合力均能够通过卫星质心的要求,并且通过此方法设计的阵列具有较强的规律性,便于准确寻址。
(2)以能够提供较大的冲量矩为标准,研究了推力器阵列在皮纳卫星上布局的方法,获得了推力器阵列安装的最优方式,当推力器阵列与阵列中心在星体坐标系中的矢量方向垂直,推力器阵列对卫星的冲量矩能够取得最大值。
(3)设计了一种基于解耦控制的正六面体布局方式,能够满足姿轨控需要,研究了该布局方式的阵列布置的包络面,能够较容易根据空间任务需要进行阵列规模设计,配置相应推力器阵列。
(References)
[1]Larangot B,Conédéra V,Dubreuil P,et al.Solid propellant microthruster:an alternative propulsion device for nanosatellite[J].Aerospace Energetic Equipment,2002:12-14:12-14
[2]张高飞,尤政,胡松启,等.基于MEMS的固体推进器阵列[J].北京.清华大学学报,2004,44(11):1489-1490
ZhangGaofei,You Zheng,Hu Songqi,et al.MEMSbased propulsion arrays with solid propellant[J].Beijing:Journal of Tsinghua University (Science and Technology),2004,44(11):1489-1490(in Chinese)
[3]Lewis D H,Janson S W,Cohen R B,et al.Digital micropropulsion[J].Sensors and Actuators:Physical,2000,80(2):143-156
[4]Rossi C,Conto D T,Esteve D,et al.Design,fabrication and modelling of MEMS-based microthrusters for space application[J].Institute of Physics Publishing.2001:1156-1162
[5]Zhang K L,Chou S K.Performance prediction of a novel solid-propellant microthruster[J].Journal of Propulsion and Power,2006,22(1):56-63
[6]Alexeenko A A,Levin A D.Girnelshein S F.Numerical study of flow structure and thrust performance for 3-D MEMS-based nozzles,AIAA 2002-3194[C]//32nd AIAA Fluid Dynamics Conference and Exhibit.Washington:AIAA,2002
[7]Jin H P,Wiktor P,Debra D B.An optimal thruster configuration design and evaluation for quick step[J].Control Eng.Practice,1995,8(3):1113-1118
[8]Durham W.Attainable moments for the contimined control allocation problem[J].Joumal of Guidance,Control and Dynamics,1994,17(6):1371-1373
[9]Bindel D.Six-dimensional thruster actuation and configuration design for spacecraft,AAS 07-021[R].Washington:AAS,2007
[10]唐生勇,张世杰,张育林,等.姿轨一体化控制航天器推力器构型设计[J].航天器控制,2010,28(3):20-28
Tang Shengyon,Zhang Shijie,Zhang Yulin,et al.Redundant thruster configuration design for the integrated orbit and attitude control of spacecraft[J].Aerospace Control.2010,28(3):20-28(in Chinese)
[11]Durham W.Attainable moments for the constrained control allocation problem [J].Journal of Guidance,Control,and Dynamics.1994,17(6):1371-1373
